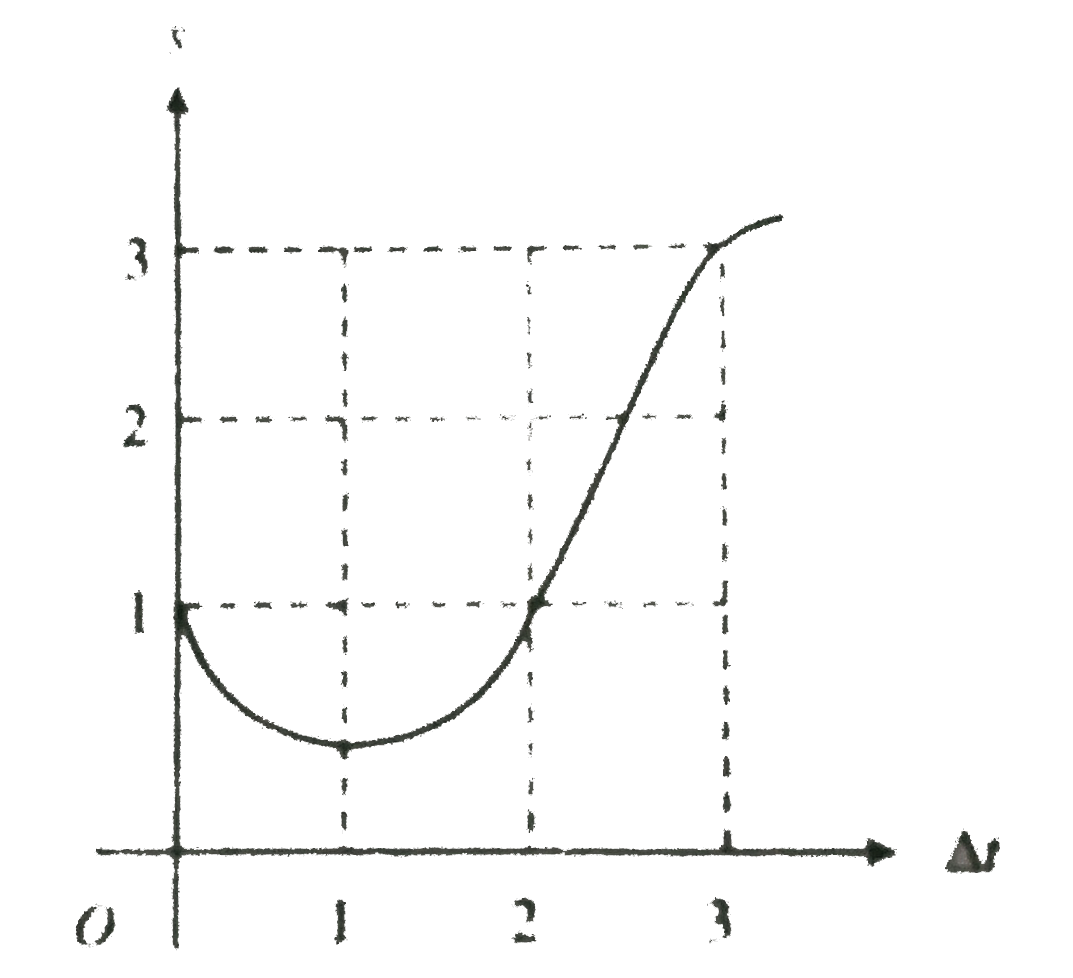
A cockroach moves rectilinearly such that after sometime t0 let its (instantaneous) velocity be equal to its average velocity over that time. Referring to the SΔt graph as shown in , for the motion of the cockroach, find the time t0 and the average velocity of the cockroach over the time t0
 .
.
since vav=v (given), the ''slope of QP=slope of the tangent PR''. Hence, QPR is a straight line.
Suppose at point ''P'' of s−t graph, both →vav and →v are equal. The average velocity during time t is given by the slope of the line QP.
That means, vav=s1−s0t0 by referring to this s−t graph. on the other hand, the velcoity v of cockroach at the time t is equal to the slope of s−t graph at the instant (point P), →v=d→sdt≡ slope of the tangent PR at P.
since →vav and →v are equal, the straight line QP must be tangential at P. Hence, the point P has coordinates (3, 3).
It gives vav=vΔsΔt=2m3s=0.67m/s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problem
14 Videos
- MOTION IN A STRAIGHT LINEBOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Problems and Practice
16 Videos
- FRICTION AND CIRCULAR MOTION BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Comprehension type
11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - GRB PUBLICATIONCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - All Questions
210 Videos
Similar Questions
Figure shows x-t graph of a particle. Find the Time T Such that the Average Velocity of the Particle During the Period 0 to T is Zero..

View SolutionA particle moves rectilinearly with initial velocity u and constant acceleration a. Find the average velocity of the particle in a time interval from t=0 to t=t second of its motion.
View Solution
Knowledge Check
Position - time graph for a particle is shown in figure. Starting from t = 0, at what time t, the average velocity is zer?
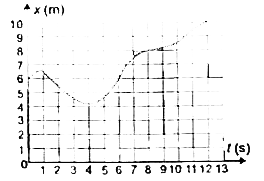 A1 sB3 sC6 sD7 s
A1 sB3 sC6 sD7 sPosition time graph is shown which is a semicircle form t=2 to t=8sec. Find time t at which the instantaneous velocity, is equal to average velocity over first t second.
 A4.8secB3.2secC2.4secD5sec
A4.8secB3.2secC2.4secD5secThe velocity time graph of a body moving along a straight line is shown in figure. The ratio of the average velocities during the time t1 and t2 is.
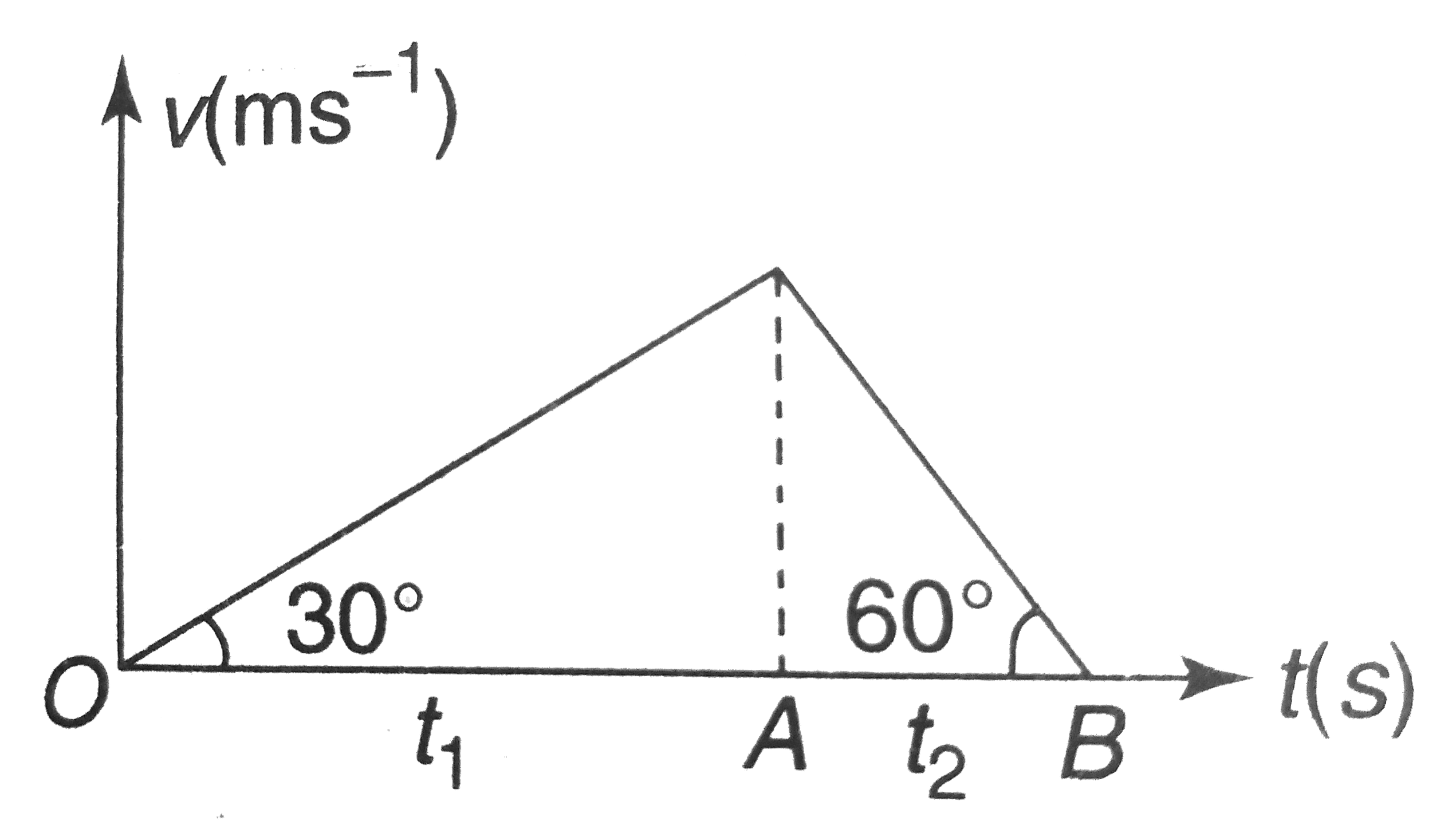 A1:1B2:1C3:1D1:3
A1:1B2:1C3:1D1:3
The velocity-time graph of a body is given below. Find the average velocity from t=0 to t=40s.

View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from t = 0 to t = 14 s, find:
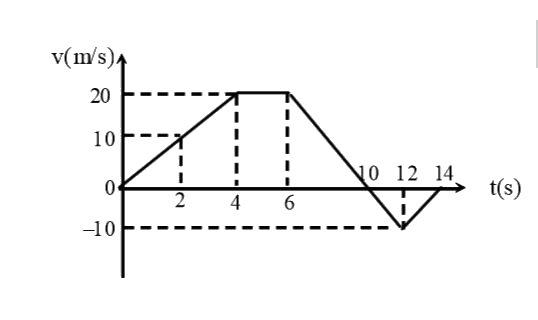
Q. average velocity and
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.
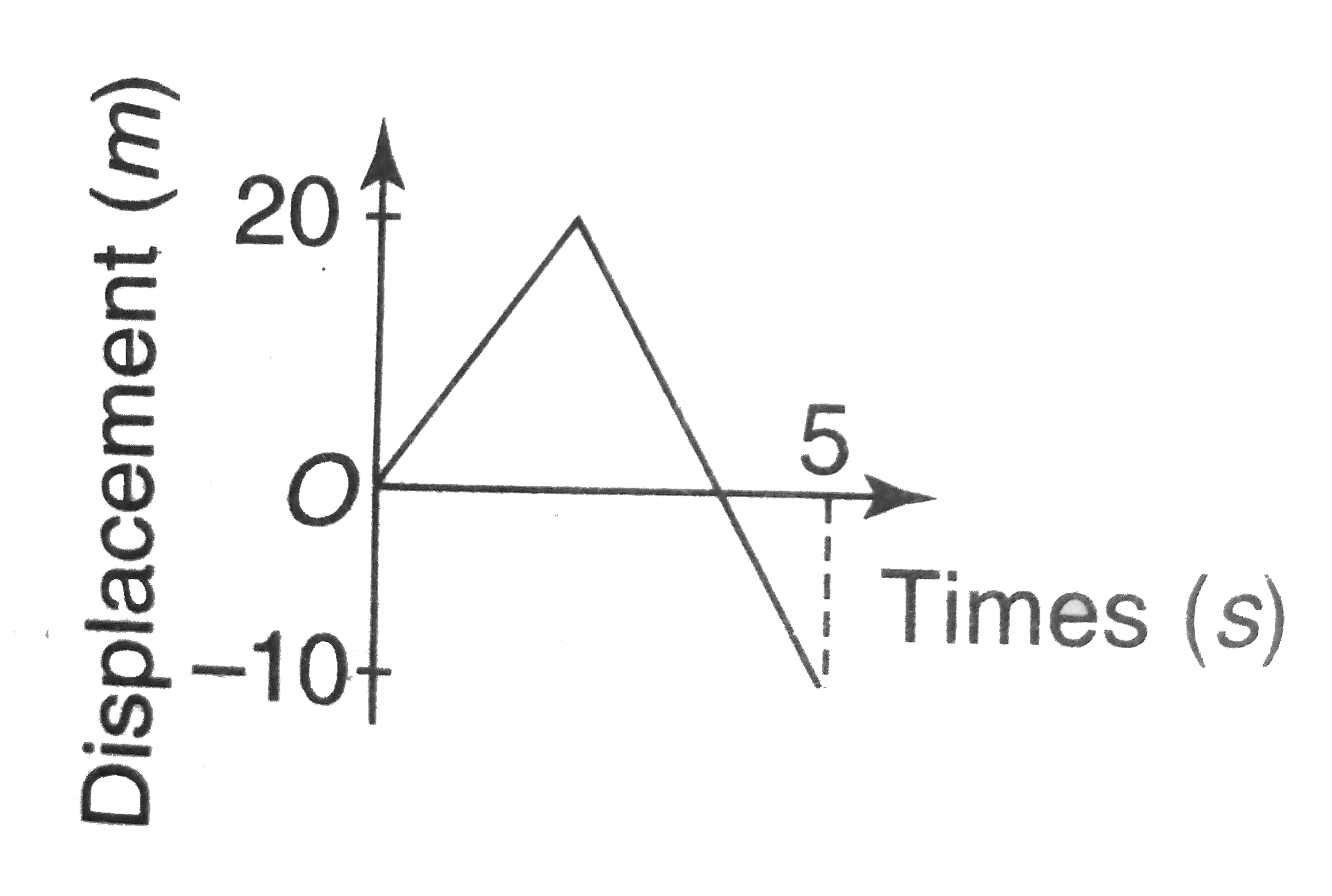
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.

View SolutionIn figure shown, the graph shows the variation of acceleration of body with time t. The velcocity of the body at t=0 is zero. The velocity of the body at t=30s is.
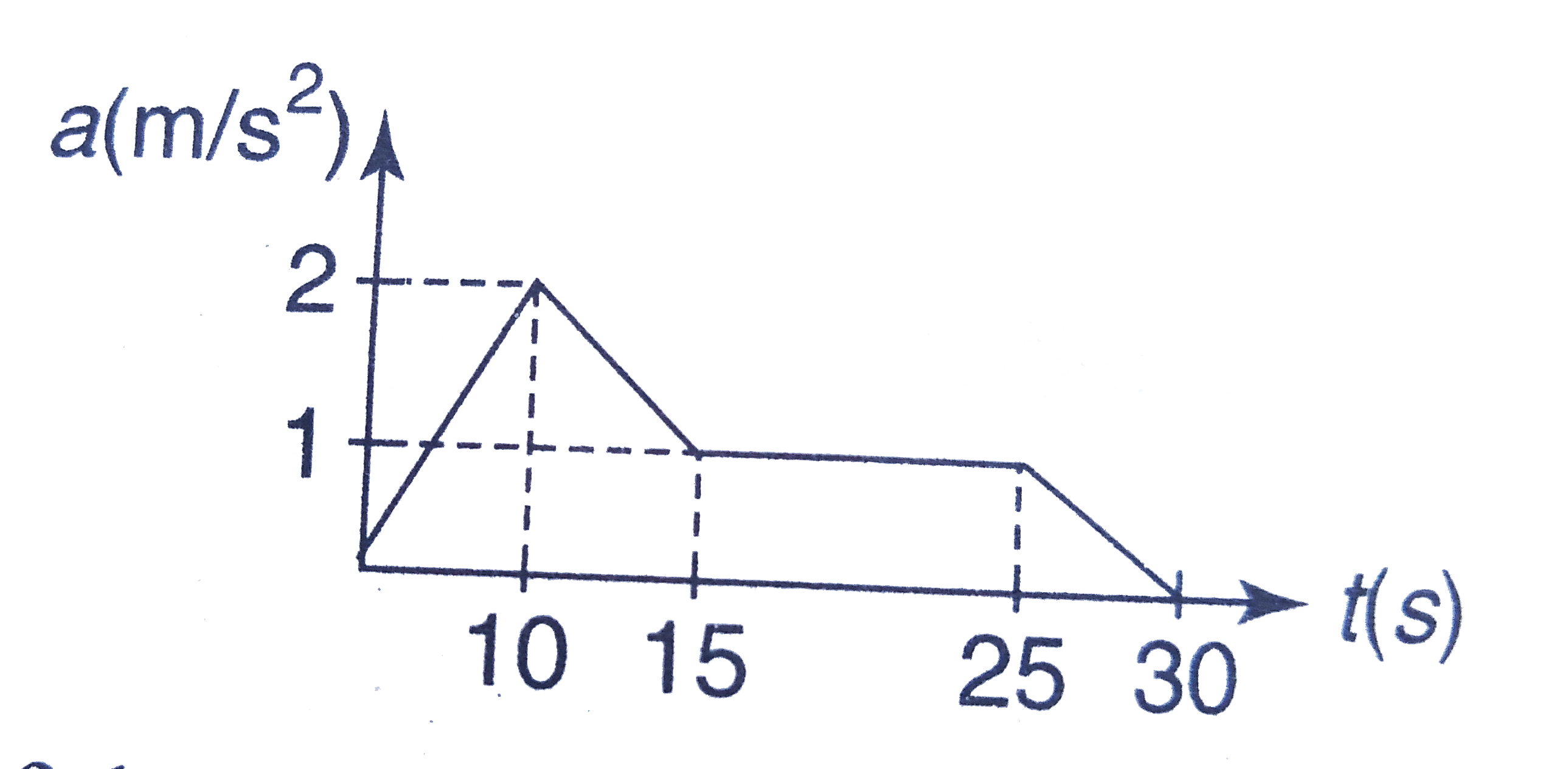
View Solution
