Consider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time $t_{1}$ , the particle is at point P, where its co-ordinate is $x_{1}$ and at time $t_{2}$ , the particle is at point Q, where its co-ordinate is $x_{2}$ . The displacement during the time interval from $t_{1}$ to $t_{2}$ is the vector from P to Q, the x-component of this vector is $(x_{2} - x_{1})$ and all other components are zero.
It is convenient to represent the quantity $x_{2} - x_{1}$ the change in x by means of a notation $Δ$ , thus $Δ x = x_{2} - x_{1}$ and $Δ t = t_{2} - t_{1}$ .

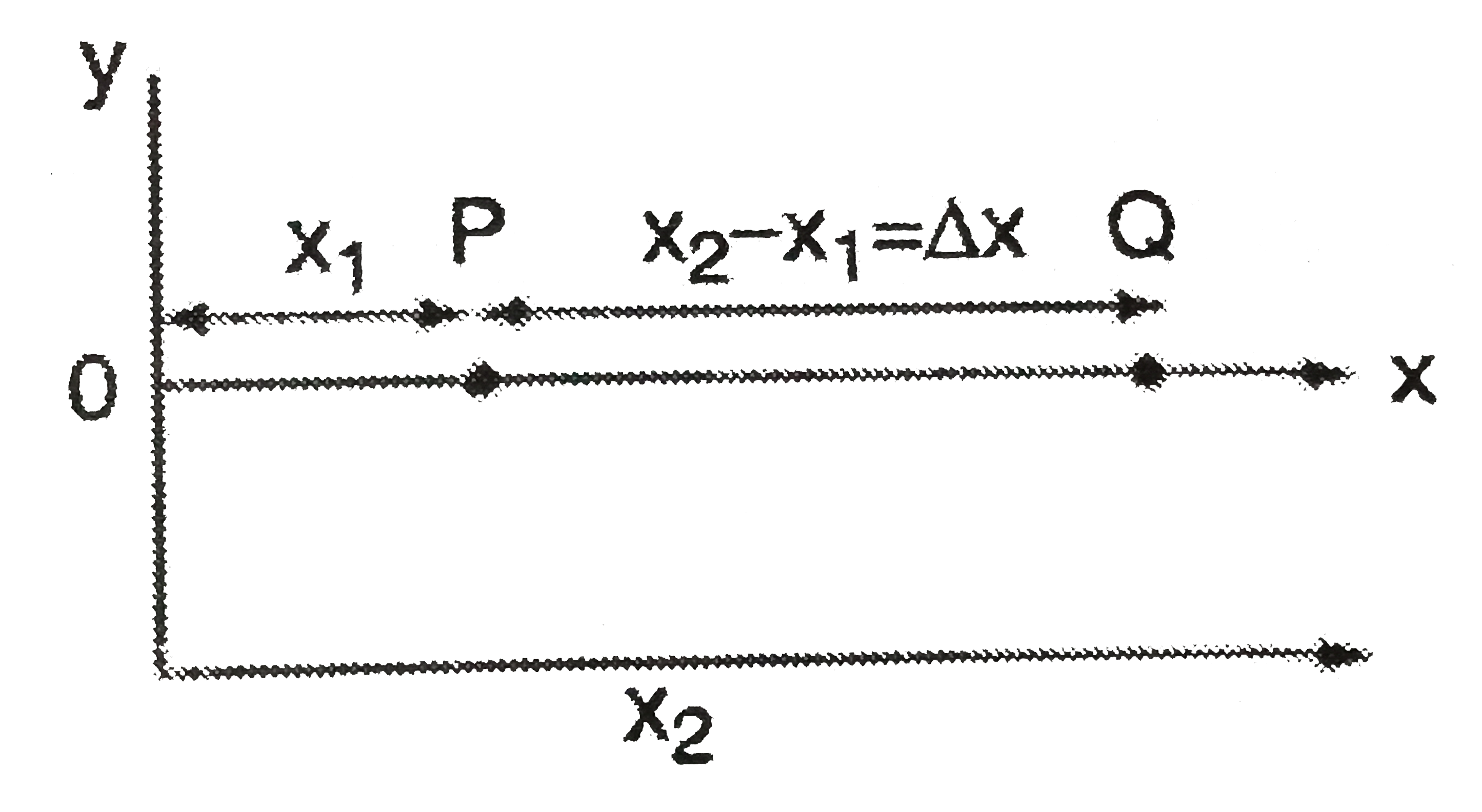
The average velocity $¯ ¯ ¯ V = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} = \frac{Δ x}{Δ t}$
A particle moves according to the equation $x = t^{2} + 3 t + 4$ . The average velocity in the first 5 s is:

8 m/s

7.6 m/s

6.4 m/s

5.8 m/s

Text Solution

Verified by Experts

The correct Answer is:A

$x = t^{2} + 3 t + 4$
$x_{1} = 4$
$x_{2} = 44$
$v_{a v} = (\frac{x_{2} - x_{1}}{Δ T})$

Updated on:21/07/2023

Class 11 PHYSICS RECTILINEAR MOTION

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
Consider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time $t_{1}$ , the particle is at point P, where its co-ordinate is $x_{1}$ and at time $t_{2}$ , the particle is at point Q, where its co-ordinate is $x_{2}$ . The displacement during the time interval from $t_{1}$ to $t_{2}$ is the vector from P to Q, the x-component of this vector is $(x_{2} - x_{1})$ and all other components are zero.
It is convenient to represent the quantity $x_{2} - x_{1}$ the change in x by means of a notation $Δ$ , thus $Δ x = x_{2} - x_{1}$ and $Δ t = t_{2} - t_{1}$ .

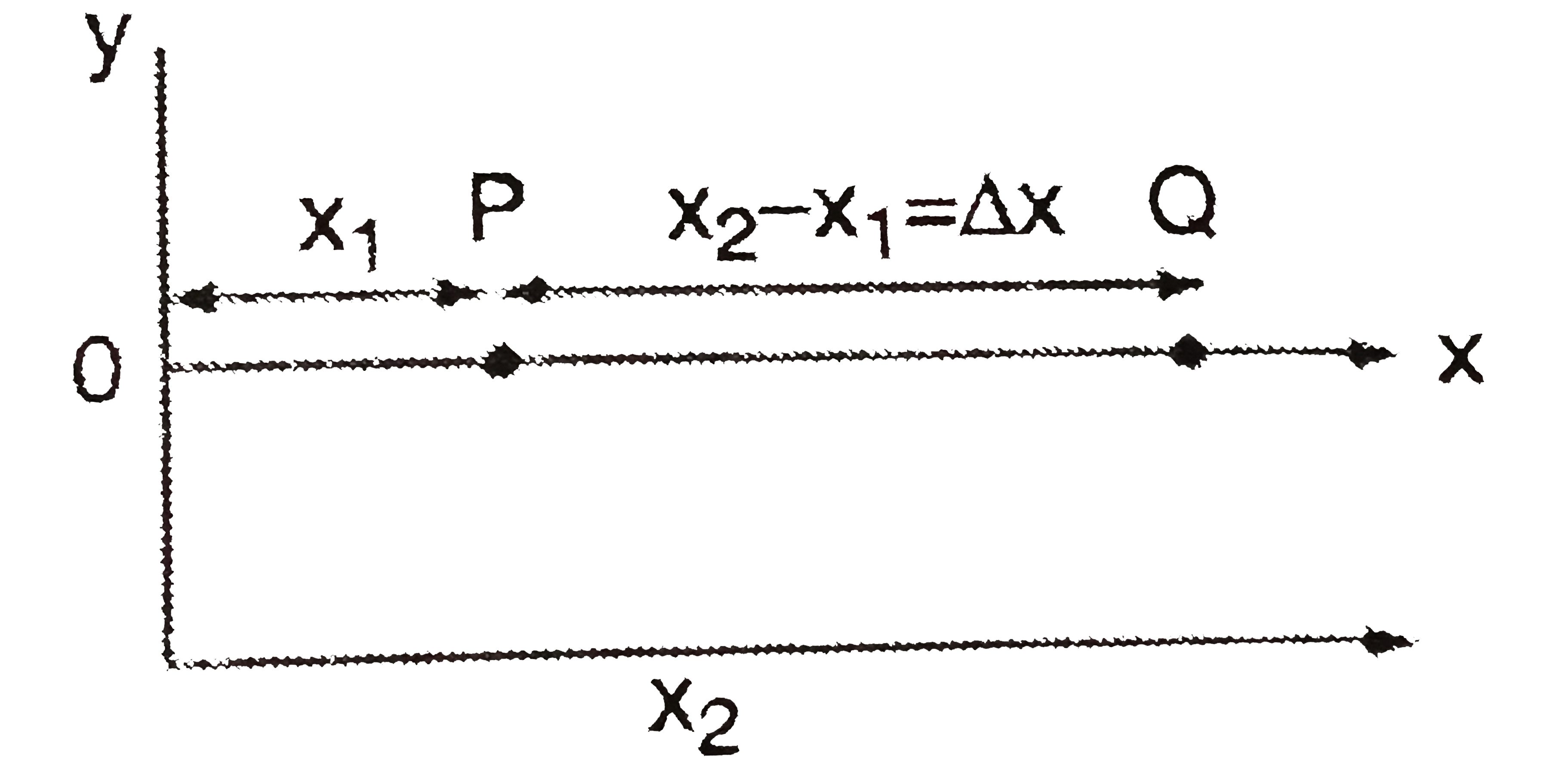
The average velocity $¯ ¯ ¯ V = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} = \frac{Δ x}{Δ t}$
A particle moves half the time of its journey with $u$ . The rest of the half time it moves with two velocities $v_{1}$ and $v_{2}$ such that half the distance it covers with $v_{1}$ and the other half with $v_{2}$ . The net average velocity is: (Assume straight line motion)
A $\frac{u (v_{1} + v_{2}) + 2 v_{1} v_{2}}{2 (v_{1} + v_{2})}$
B $\frac{2 u (v_{1} + v_{2})}{2 u + v_{1} + v_{2}}$
C $\frac{u (v_{1} + v_{2})}{2 v_{1}}$
D $\frac{2 v_{1} v_{2}}{u + v_{1} + v_{2}}$
Question 2 - Select One
Consider a particle moving along x-axis. Its distance from origin O is described by the co-ordinate x which varies with time. At a time $t_{1}$ , the particle is at point P, where its co-ordinate is $x_{1}$ and at time $t_{2}$ , the particle is at point Q, where its co-ordinate is $x_{2}$ . The displacement during the time interval from $t_{1}$ to $t_{2}$ is the vector from P to Q, the x-component of this vector is $(x_{2} - x_{1})$ and all other components are zero.
It is convenient to represent the quantity $x_{2} - x_{1}$ the change in x by means of a notation $Δ$ , thus $Δ x = x_{2} - x_{1}$ and $Δ t = t_{2} - t_{1}$ .

The average velocity $¯ ¯ ¯ V = \frac{x_{2} - x_{1}}{t_{2} - t_{1}} = \frac{Δ x}{Δ t}$
The resistive force suffered by a motor boat is proportional to $v^{2}$ , where $v$ is instantaneous velocity. The engine was shut down when the velocity of the boat was $v_{0}$ . Find the average velocity at any time $t$ .
A $\frac{v_{0} + v}{2}$
B $\frac{v v_{0}}{2 (v_{0} + v)}$
C $\frac{v v_{0} {log}_{e} (\frac{v_{0}}{v})}{(v_{0} - v)}$
D $\frac{2 v v_{0} {log}_{e} (\frac{v_{0}}{v})}{(v_{0} + v)}$
Question 3 - Select One or More
A particle is moving along $x$ -axis. Its velocity $v$ with $x$ co-ordinate is varying as $v = \sqrt{x}$ . Then
Ainitial velocity of particle is zero
Bmotion is non-uniformly accelerated
Cacceleration of particle at $x = 2 m$ is $\frac{1}{2} m / s^{2}$
Dacceleration of particle at $x = 4 m$ is $1 m / s^{2}$