A coil formed by wrapping 50 turns of wire in the shape of a square is positioned in a magnetic field so that the normal to the plane of the coil makes an angle of 30∘. with the direction of the field. When the magnetic field is increased uniformly from 200μT to 600μT in 0.4s, an emf of magnitude 80.0 mV is induced in the coil. What is the total length of the wire?
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the Problem
We have a coil with 50 turns, shaped as a square, placed in a magnetic field. The magnetic field changes from 200 µT to 600 µT in 0.4 seconds, inducing an emf of 80.0 mV in the coil. We need to find the total length of the wire used in the coil.
Step 2: Calculate the Change in Magnetic Field
The change in magnetic field (ΔB) can be calculated as:
ΔB=Bf−Bi=600μT−200μT=400μT=400×10−6T
Step 3: Calculate the Rate of Change of Magnetic Field
The rate of change of the magnetic field (dB/dt) is given by:
dBdt=ΔBΔt=400×10−6T0.4s=1000×10−6T/s=1mT/s
Step 4: Calculate the Induced EMF
The induced emf (ε) in the coil can be expressed as:
ϵ=−NdΦdt
Where N is the number of turns and Φ is the magnetic flux. The magnetic flux (Φ) is given by:
Φ=B⋅A⋅cos(θ)
Here, A is the area of the coil and θ is the angle between the magnetic field and the normal to the coil (30 degrees).
Step 5: Relate Induced EMF to Area
From the induced emf equation:
ϵ=N⋅A⋅cos(30∘)⋅dBdt
Substituting the known values:
80×10−3=50⋅A⋅cos(30∘)⋅1×10−3
Using cos(30∘)=√32:
80×10−3=50⋅A⋅√32⋅1×10−3
Step 6: Solve for Area (A)
Rearranging the equation gives:
A=80×10−350⋅√32⋅1×10−3=8050⋅√32=80⋅250√3=16050√3=165√3m2
Step 7: Calculate Side Length of the Square
Since the area of the square is A=s2:
s=√A=√165√3
Calculating this gives:
s≈1.36m
Step 8: Calculate the Total Length of the Wire
The perimeter (P) of the square is given by:
P=4s
Thus, the total length of the wire (L) for 50 turns is:
L=50⋅P=50⋅4s=200s
Substituting the value of s:
L=200⋅1.36≈272m
Final Answer
The total length of the wire is approximately 272 meters.
---
We have a coil with 50 turns, shaped as a square, placed in a magnetic field. The magnetic field changes from 200 µT to 600 µT in 0.4 seconds, inducing an emf of 80.0 mV in the coil. We need to find the total length of the wire used in the coil.
The change in magnetic field (ΔB) can be calculated as:
ΔB=Bf−Bi=600μT−200μT=400μT=400×10−6T
The rate of change of the magnetic field (dB/dt) is given by:
dBdt=ΔBΔt=400×10−6T0.4s=1000×10−6T/s=1mT/s
The induced emf (ε) in the coil can be expressed as:
ϵ=−NdΦdt
Where N is the number of turns and Φ is the magnetic flux. The magnetic flux (Φ) is given by:
Φ=B⋅A⋅cos(θ)
Here, A is the area of the coil and θ is the angle between the magnetic field and the normal to the coil (30 degrees).
From the induced emf equation:
ϵ=N⋅A⋅cos(30∘)⋅dBdt
Substituting the known values:
80×10−3=50⋅A⋅cos(30∘)⋅1×10−3
Using cos(30∘)=√32:
80×10−3=50⋅A⋅√32⋅1×10−3
Rearranging the equation gives:
A=80×10−350⋅√32⋅1×10−3=8050⋅√32=80⋅250√3=16050√3=165√3m2
Since the area of the square is A=s2:
s=√A=√165√3
Calculating this gives:
s≈1.36m
The perimeter (P) of the square is given by:
P=4s
Thus, the total length of the wire (L) for 50 turns is:
L=50⋅P=50⋅4s=200s
Substituting the value of s:
L=200⋅1.36≈272m
The total length of the wire is approximately 272 meters.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Single Correct37videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct10videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions3videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
A coil of 100 turns and area 5 square centimetre is placed in a magnetic field B = 0.2 T . The normal to the plane of the coil makes an angle of 60∘ with the direction of the magnetic field. The magnetic flux linked with the coil is
View SolutionA coil of area 5cm2 and having 20 turns is placed in a uniform magnetic field of 103 gauss. The normal to the plane of the coil makes an angle of 60∘ with the magnetic field. The flux in Maxwell through the coil is:
View Solution
Knowledge Check
- Question 1 - Select One
A square coil of side 10cm consists of 20 turns and carries a current of 12A. The coil is suspended vertically and normal to the plane of the coil makes an angle of 30∘ with the direction of a uniform horizontal magnetic field of magnitude 0⋅80T. What is the magnitude of torque experienced by the coil?
A1.6 N mB1.2 N mC1.4 N mD1.8 N m - Question 2 - Select One
A circular coil of 25 turns and radius 12 cm is placed in a uniform magnetic field of 0.5 T normal to the plane of the coil. If the current in the coil is 6 A then total torque acting on the coil is
AzeroB3.4 NmC3.8 NmD4.4 Nm
A coil of area 5cm2 and having 20 turns is placed in a uniform magnetic field of 103 gauss. The normal to the plane of the coil makes an angle of 60∘ with the magnetic field. The flux in Maxwell through the coil is:
View SolutionA coil is placed in a constant magnetic field. The magnetic field is parallel to the plane of the coil as shown in Fig. 3.28. Find the emf induced in the coil if B increasing.
 View Solution
View SolutionA coil of 100 turns, 5cm2 area is placed in external magnetic field of 0.2 Tesla (S.I) in such a way that plane of the coil makes an angle 30∘ with the field direction. Calculate magnetic flux of the coil (in weber)
View SolutionFind the emf induced in the coil shown in figure.The magnetic field is perpendicular to the plane of the coil and is constant.
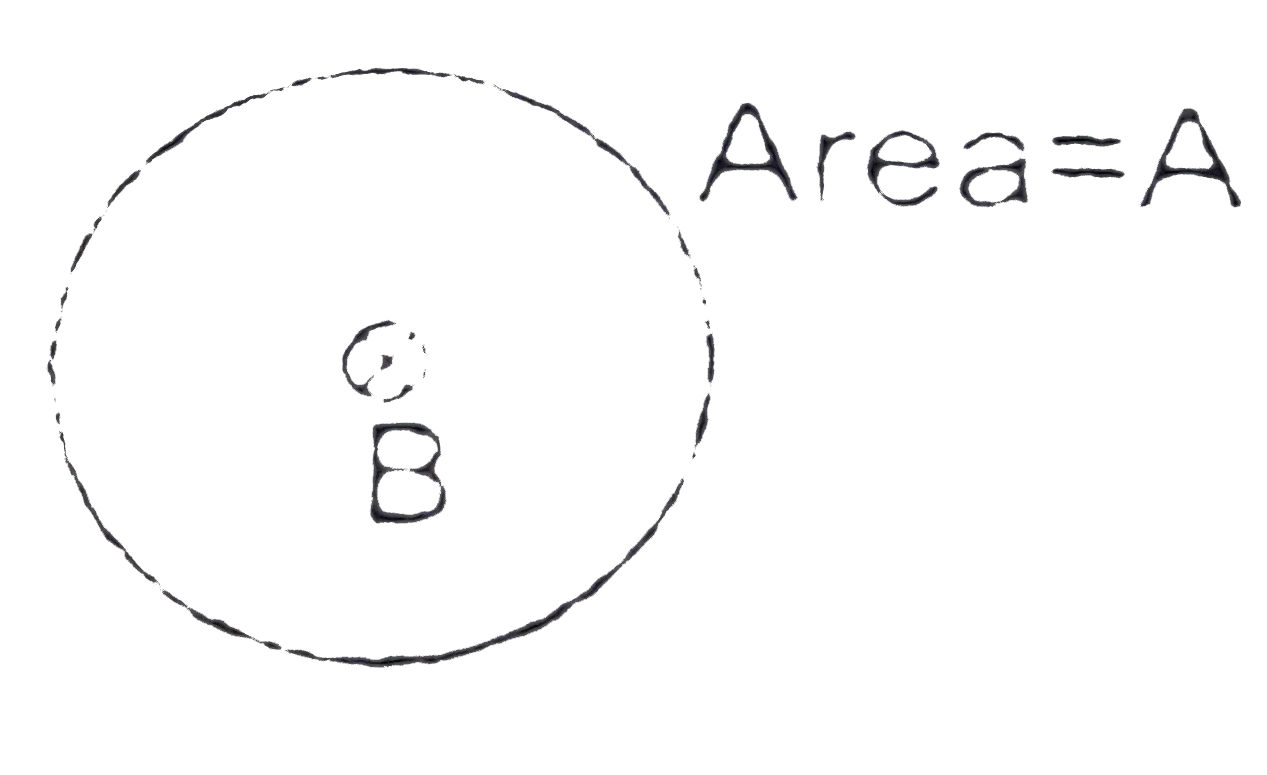 View Solution
View SolutionA square coil of side 10cm consists of 20 turns and carries a current of 12A. The coil is suspended vertically and normal to the plane of the coil makes an angle of 30∘ with the direction of a uniform horizontal magnetic field of magnitude 0⋅80T. What is the magnitude of torque experienced by the coil?
View SolutionA rectangular coil is placed in a region having a uniform magnetic field B perpendicular to the plane of the coil. An emf will not be induced ion the coil if the
 View Solution
View Solution

