A coil of Cu wire (radius r, self-inductance L) is bent in two concentric turns each having radius r2. The self-inductance now
2L
L
4L
L/2
The correct Answer is:A
To solve the problem, we need to determine the self-inductance of a coil after it has been bent into two concentric turns. Here’s a step-by-step solution:
Step 1: Understand the relationship between self-inductance, number of turns, and radius
The self-inductance L of a coil is given by the formula:
L∝n2⋅r
where n is the number of turns and r is the radius of the coil.
Step 2: Identify the initial conditions
Initially, we have:
- Self-inductance before bending: L1=L
- Radius before bending: r1=r
- Number of turns before bending: n1=1 (since it's a single coil)
Step 3: Identify the new conditions after bending
After bending the coil into two concentric turns:
- New radius: r2=r2
- New number of turns: n2=2 (since it is now two turns)
Step 4: Write the relationship for self-inductance after bending
Using the relationship for self-inductance, we can write:
L1L2=n21⋅r1n22⋅r2
Step 5: Substitute the known values
Substituting the values we have:
LL2=(1)2⋅r(2)2⋅(r2)
This simplifies to:
LL2=r4⋅r2=r2r=12
Step 6: Solve for L2
From the above equation, we can express L2:
L2=2L
Conclusion
The self-inductance after bending the coil is:
L2=2L
Final Answer
The correct option is option number 1: 2L.
---
The self-inductance L of a coil is given by the formula:
L∝n2⋅r
where n is the number of turns and r is the radius of the coil.
Initially, we have:
- Self-inductance before bending: L1=L
- Radius before bending: r1=r
- Number of turns before bending: n1=1 (since it's a single coil)
After bending the coil into two concentric turns:
- New radius: r2=r2
- New number of turns: n2=2 (since it is now two turns)
Using the relationship for self-inductance, we can write:
L1L2=n21⋅r1n22⋅r2
Substituting the values we have:
LL2=(1)2⋅r(2)2⋅(r2)
This simplifies to:
LL2=r4⋅r2=r2r=12
From the above equation, we can express L2:
L2=2L
The self-inductance after bending the coil is:
L2=2L
The correct option is option number 1: 2L.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Multiple Correct Answer3videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Comprehension Type8videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - INDUCTANCEEXERCISE - Subective Type2videos
INDUCTANCE
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - HEATING EFFECT OF CURRENTEXERCISE - Thermal Power in Resistance Connected in Circuit27videos
HEATING EFFECT OF CURRENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
Similar Questions
A long solenoid has self inductance. L. If its length is doubled keeping total number of turns constant then its new self inductance will be
View SolutionA wire of fixed length is wound on a solenoid of length l and radius r. Its self-inductance is found to be L. Now, if the same wire is wound on a solenoid of length l/2 and radius r/2 then the self-inductance will be
View SolutionA solenoid have self inductance 2H. If length of the solenoid is double having turn density and area constant then new self inductance is :-
View SolutionThe inductors of self inductance L1 and L2 are put in series .
View SolutionThree solenoid coils of same dimension, same number of turns and same number of layers of windings are taken. Coil 1 with inductance L1 was would using a wire of resistance 11Ω/m, coil 2 with inductance L2 was wound using the similar wire but the direction of winding was reversed in each layer, coil 3 with inductance L3 was wound using a superconducting wire. The self-inductance of the coils L1,L2 and L3 are
View SolutionThe self-inductances of two identical coils are 0.1H. They are wound over each other. Mutual inductance will be-
View SolutionTwo pure inductors each of self-inductance L are connected in parallel but are well separted from each other. The total inductance is
View SolutionThe self inductance L of a solenoid depends on the number of turns per unit length 'n' as
View SolutionThe self inductance of a solenoid of length L, area of cross-section A and having N turns is-
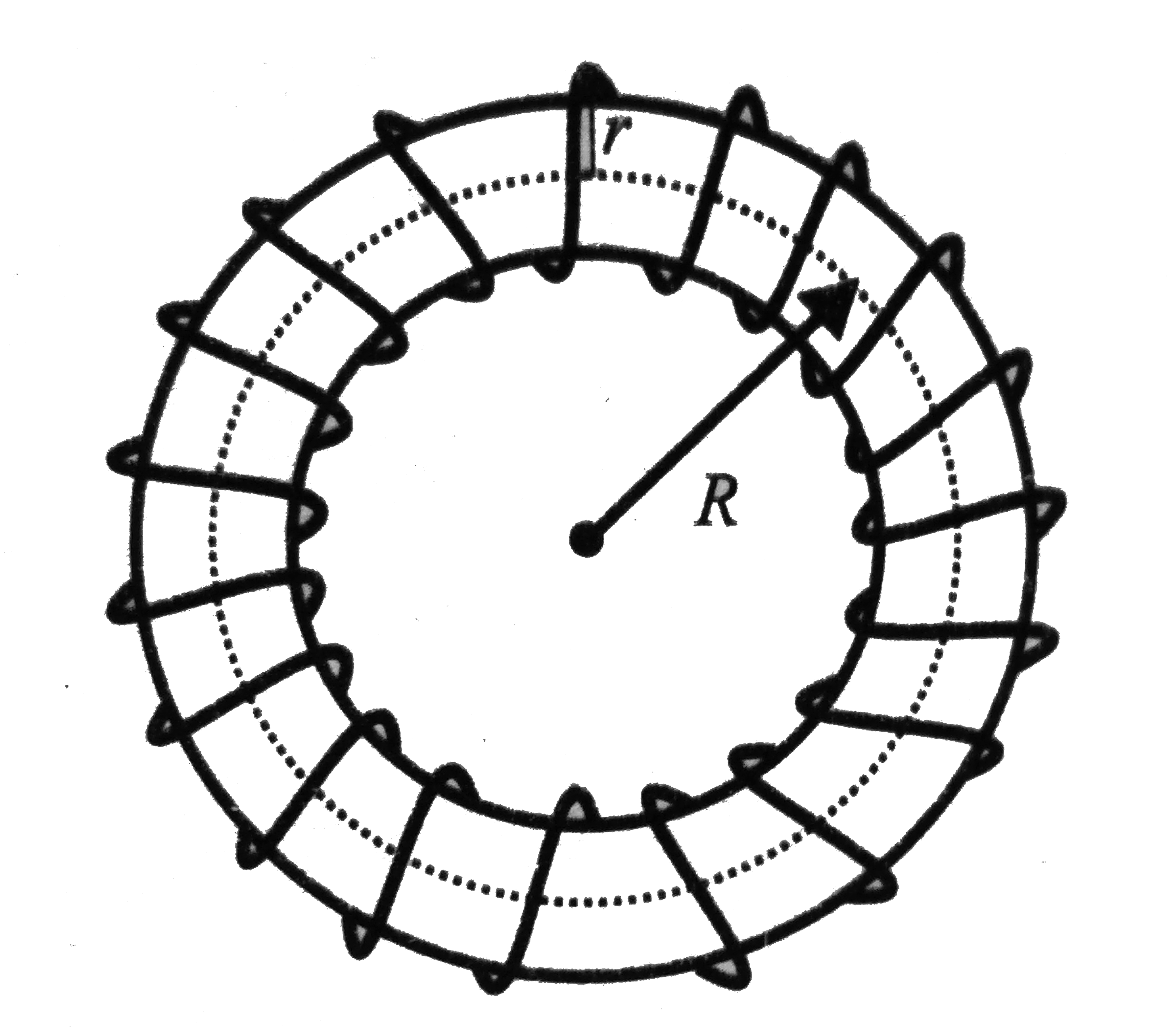
View SolutionA toroid is wound over a circular core. Radius of each turn is r and radius of toroid is R(>>r). The coefficient of self-inductance of the toroid is given by
 View Solution
View Solution

