A coil of inductance L connects the upper ends of two vertical copper bars separated by a distance l . A horizontal conducting connnector of mass m starts falling with zero initial velocit along the bars without losing contact with them. The whole system is located in a uniform magnetic field with induction B perpendicular to the plane of the bars. Find the law of motion x(t) of the connector.
As the connector moves, an emf is set up in the cirucuit and a current flows, since the emf is ξ=−Bl.x, we must have :−Bl.x+LdIdt=0
so, I=Blx/L
provided x is measured from the initial position.
We then have
m..x=−BlxL.B.l+mg
for by Lenz's law the induced current will oppose downward sliding . Final
..x+(Bl)2mLx=g
on putting ω0=Bl√mL
..x+ω20x=g
A solution of this equation is x=gω20+Acos(ω0t+α)
Butx=0 and .x=0 at t=0. This gives
x=gω20(1−cosω0t).

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electric Oscillations
56 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves
39 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise
2 Videos
- PHYSICAL FUNDAMENTALS OF MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics
49 Videos
Similar Questions
A coil of inductance L connects the upper ends of two vertical copper bars separated by a distance l . A horizontal conducting connector of mass m starts falling with zero initial velocity along the bars without losing contact with them. The whole system is located in a uniform magnetic field B perpendicular to the plane of the bars. Find the law of motion x(t) of the connector.

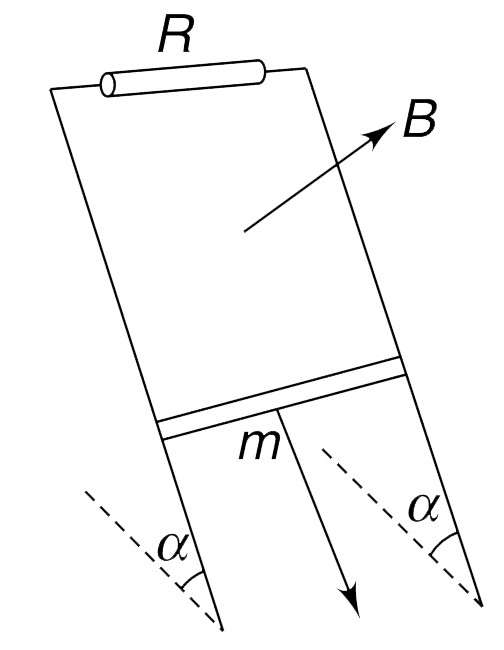
View SolutionA copper connector of massm, starting from rest, slides down two conducting bars set at angle α to the horizontal, due to gravity (see figure). At the top the bars are interconnected trhough a resistance R. The separation between the bars is equal to l. The system is located in uniform magnetic field of induction B, perpendicular to the plane in which the connectr slides. The resistance of the bars the connector and the sliding contacts, as well as the self inductance of the loop, are assumed to be negligible. The coefficient of friction between the connector and the bars is equal to 12 and α
(a) Find the steady-state velocity of the connector.
(b) How will your answer differ if the magnetic field was in opposite direction.
View Solution
Knowledge Check
In case of a bar magnet, lines of magnetic induction
Astart form the south pole and end at the north pole .Brun continously through the bar magnet and outside.Cemerge in circular paths from the middle of the barDare produced only at the north pole like rays of light form a bulba conducting wire os mass m slides down two smooth conducting bars, set at an angle θ to the horizontal as shown in . The separatin between the bars is l. The system is located in the magnetic field B, perpendicular to the plane of the sliding wire and bars. The constant velocity of the wire is
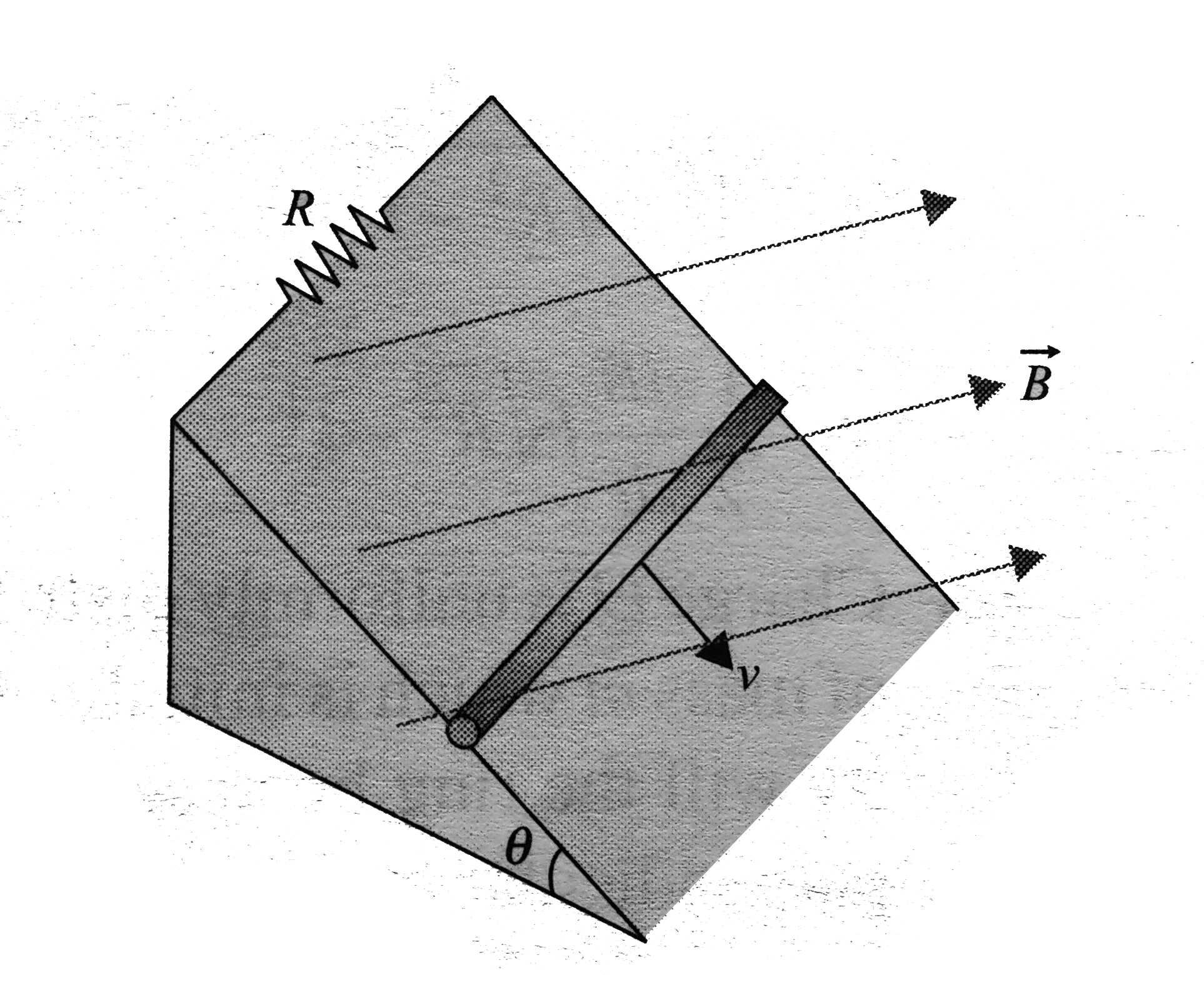 A(a) mgRsinθB2l2B(b) mgRsinθBl3C( c) mgRθB2l5D( d) mgRsinθBl4
A(a) mgRsinθB2l2B(b) mgRsinθBl3C( c) mgRθB2l5D( d) mgRsinθBl4A copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
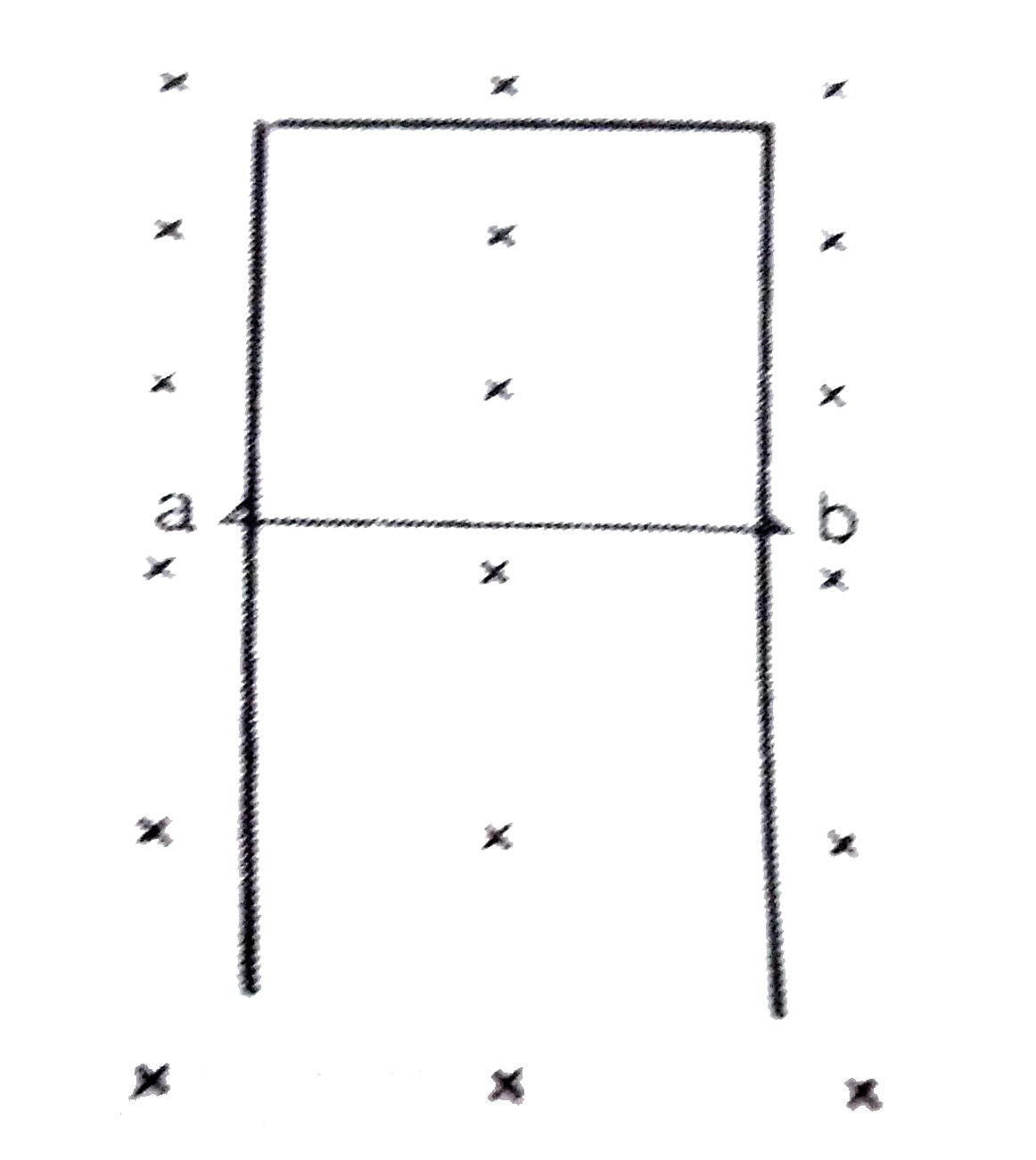 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
A copper connector of mass m slides down two smooth cooper bars, set at an angle α to the horizontal due to gravity (Fig). At the top the bars is equal to l. The system is located in a unifrom magnetic field of induction B, perpendicular to the plane in which the connector slides. The resistances of the bars, the connector and the sliding contacts, as well as the self-inductance of the loop, are assumed to be negligible. Find the steady-state velocity of the connector.

View SolutionA copper bar of mass m sides under gravity on two smooth parallel rails l distance apart and set at angle α to the horizontal . At the lop , the rails are joined by a resistor R. Calculate the steady velocity of the bar the n when there is a unifrom magnetic field B perpedicular to the plane of the rails .
View SolutionIn the case of bar magnet, lines of magnetic induction
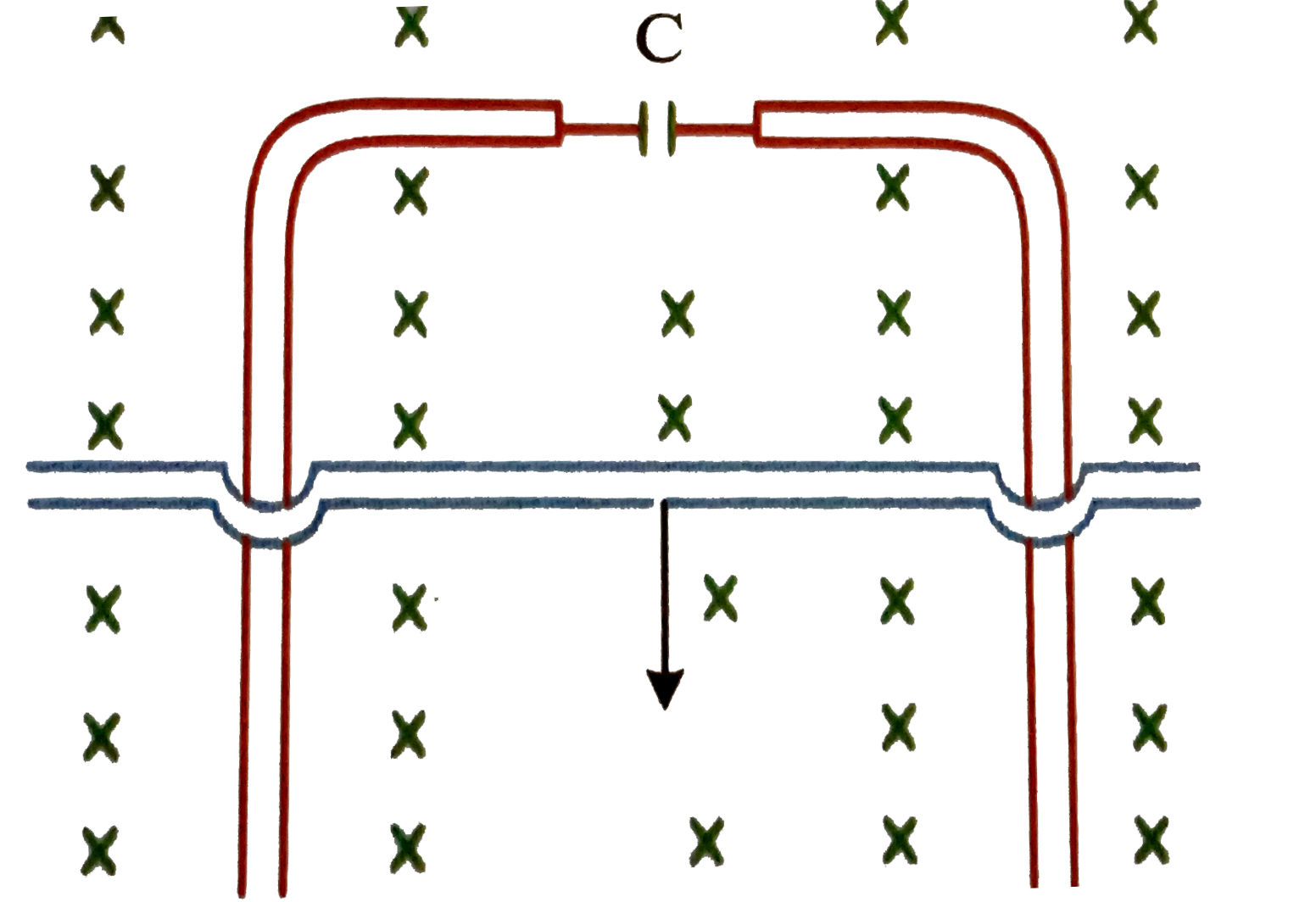
View SolutionA conducting wire of length l and mass m can slide without friction on two parallel rails and is connected to capacitance C. The whole system lies in a magnetic field B and a constant force F is applied to the rod. Then
View SolutionA conductor of length l and mass m can slide without any friction along the two vertical conductors connected at the top through a capacitor. A uniform magnetic field B is set up ⊥ to the plane of paper. The acceleration of the conductor
View Solution
