A coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. Is induced in the coil.
To determine whether the statement "A coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. is induced in the coil." is true or false, we can follow these steps:
Step 1: Understand the situation
We have a coil of metal wire that is stationary in a non-uniform magnetic field. A non-uniform magnetic field means that the magnetic field strength varies in different regions of the field.
Hint: Consider what it means for a magnetic field to be non-uniform and how it might affect the coil.
Step 2: Analyze the magnetic flux
Magnetic flux (Φ) through the coil is given by the product of the magnetic field (B) and the area (A) through which it passes, as well as the angle (θ) between the magnetic field and the normal to the surface of the coil. In this case, even though the magnetic field is non-uniform, the coil is stationary, meaning that the area and orientation of the coil remain constant.
Hint: Recall the formula for magnetic flux: Φ = B * A * cos(θ).
Step 3: Determine if the magnetic flux is changing
Since the coil is stationary and the area and orientation do not change, we need to check if the magnetic flux is changing over time. The magnetic flux through the coil will remain constant even though the magnetic field strength varies in different parts of the field.
Hint: Think about how a change in magnetic flux is related to the movement of the coil or a change in the magnetic field over time.
Step 4: Apply Faraday's Law of Electromagnetic Induction
According to Faraday's Law, the induced electromotive force (e.m.f.) in a coil is proportional to the rate of change of magnetic flux through the coil:
e.m.f.=−dΦdt
Since the magnetic flux (Φ) is constant (not changing), we have:
dΦdt=0
Thus, the induced e.m.f. will be:
e.m.f.=−0=0
Hint: Remember that the induced e.m.f. is related to the change in magnetic flux.
Step 5: Conclusion
Since the induced e.m.f. is zero, we conclude that no e.m.f. is induced in the coil despite the non-uniformity of the magnetic field. Therefore, the statement "An e.m.f. is induced in the coil" is false.
Final Answer: The statement is false.
We have a coil of metal wire that is stationary in a non-uniform magnetic field. A non-uniform magnetic field means that the magnetic field strength varies in different regions of the field.
Magnetic flux (Φ) through the coil is given by the product of the magnetic field (B) and the area (A) through which it passes, as well as the angle (θ) between the magnetic field and the normal to the surface of the coil. In this case, even though the magnetic field is non-uniform, the coil is stationary, meaning that the area and orientation of the coil remain constant.
Since the coil is stationary and the area and orientation do not change, we need to check if the magnetic flux is changing over time. The magnetic flux through the coil will remain constant even though the magnetic field strength varies in different parts of the field.
According to Faraday's Law, the induced electromotive force (e.m.f.) in a coil is proportional to the rate of change of magnetic flux through the coil:
e.m.f.=−dΦdt
Since the magnetic flux (Φ) is constant (not changing), we have:
dΦdt=0
Thus, the induced e.m.f. will be:
e.m.f.=−0=0
Since the induced e.m.f. is zero, we conclude that no e.m.f. is induced in the coil despite the non-uniformity of the magnetic field. Therefore, the statement "An e.m.f. is induced in the coil" is false.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Single Correct
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Archives Multiple Correct
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Integer
9 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
Knowledge Check
Choose the correct option:
A rectangular coil of copper wires is rotated in a magnetic field. The direction of the induced current changes once in each:Aone revolutionB12 revolutionC14 revolutionD2 revolution
A magnetic needle is kept in a non uniform magnetic field . It experiences
View SolutionA magnetic needle is kept in a non uniform magnetic field . It experiences
View SolutionA glass rod of length l moves with velocity v in a uniform magnetic field B. What is the e.m.f induced in the rod?
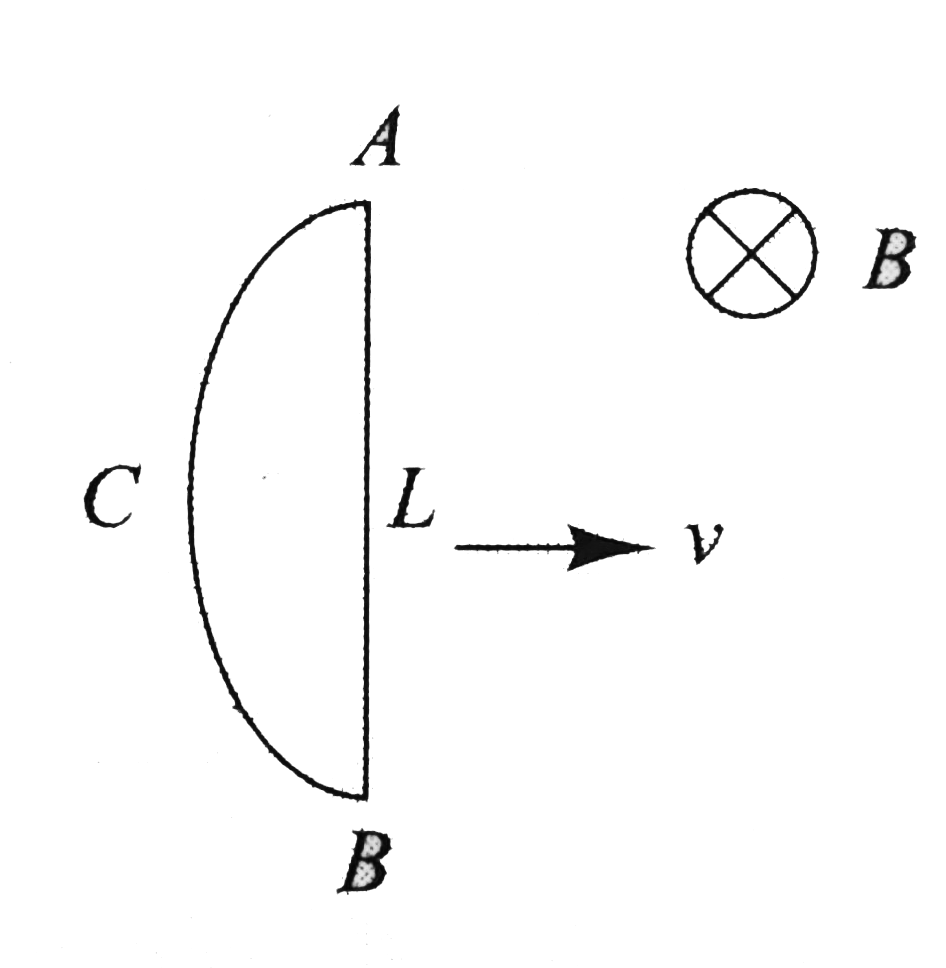
View SolutionShows a closed coil ABCL moving in a uniform magnetic field B with a velocity v.
Find
(a) emf induced in the coil.
(b) emf induced in curve part ACB and straight AB
View SolutionA coil of N turns and mean cross-sectional area A is rotating with uniform angular velocity ω about an axis at right angle to uniform magnetic field B. The induced emf E in the coil will be
View SolutionA coil carrying electric current is placed in uniform magnetic field
View Solution(A): When a conducting wire loop which is inside a uniform magnetic field directed perpendicular to its planes is moving with uniform velocity, an e.m.f is induced in it.
(R) : When magnetic flux linked with a conducting wire loop changes with time an e.m.f is induced in the coil.
View Solution
