A coil of N turns and mean cross-sectional area A is rotating with uniform angular velocity ω about an axis at right angle to uniform magnetic field B. The induced emf E in the coil will be
NBAsinωt
NBωsinωt
NB/Asinωt
NBAωsinωt
The correct Answer is:D
To solve the problem of finding the induced EMF E in a rotating coil, we can follow these steps:
Step 1: Understand the Setup
We have a coil with N turns and a mean cross-sectional area A rotating in a uniform magnetic field B with an angular velocity ω. The axis of rotation is perpendicular to the magnetic field.
Step 2: Determine the Angle
As the coil rotates, the angle θ between the area vector of the coil and the magnetic field changes over time. The angle can be expressed as:
θ(t)=ωt
where ω is the angular velocity and t is time.
Step 3: Calculate Magnetic Flux
The magnetic flux Φ through the coil at any instant is given by:
Φ=N⋅B⋅A⋅cos(θ)
Substituting θ(t):
Φ=N⋅B⋅A⋅cos(ωt)
Step 4: Find the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is equal to the negative rate of change of magnetic flux:
E=−dΦdt
Now, we differentiate the expression for magnetic flux:
E=−ddt(N⋅B⋅A⋅cos(ωt))
Using the chain rule, we find:
E=−N⋅B⋅A⋅ddt(cos(ωt))
The derivative of cos(ωt) is:
ddt(cos(ωt))=−ωsin(ωt)
Thus, substituting this back, we have:
E=−N⋅B⋅A⋅(−ωsin(ωt))
This simplifies to:
E=N⋅B⋅A⋅ωsin(ωt)
Final Answer
The induced EMF E in the coil is given by:
E=N⋅B⋅A⋅ωsin(ωt)
---
We have a coil with N turns and a mean cross-sectional area A rotating in a uniform magnetic field B with an angular velocity ω. The axis of rotation is perpendicular to the magnetic field.
As the coil rotates, the angle θ between the area vector of the coil and the magnetic field changes over time. The angle can be expressed as:
θ(t)=ωt
where ω is the angular velocity and t is time.
The magnetic flux Φ through the coil at any instant is given by:
Φ=N⋅B⋅A⋅cos(θ)
Substituting θ(t):
Φ=N⋅B⋅A⋅cos(ωt)
According to Faraday's law of electromagnetic induction, the induced EMF E is equal to the negative rate of change of magnetic flux:
E=−dΦdt
Now, we differentiate the expression for magnetic flux:
E=−ddt(N⋅B⋅A⋅cos(ωt))
Using the chain rule, we find:
E=−N⋅B⋅A⋅ddt(cos(ωt))
The derivative of cos(ωt) is:
ddt(cos(ωt))=−ωsin(ωt)
Thus, substituting this back, we have:
E=−N⋅B⋅A⋅(−ωsin(ωt))
This simplifies to:
E=N⋅B⋅A⋅ωsin(ωt)
The induced EMF E in the coil is given by:
E=N⋅B⋅A⋅ωsin(ωt)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Taking it together
119 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrance special format questions
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example
71 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
Knowledge Check
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
A conducting rod of length l is rotating with constant angular velocity ω about point O in a uniform magnetic field B as shown in the figure . What is the emf induced between ends P and Q ?

View SolutionA semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is

View SolutionA square loop of edge b having M turns is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field B0 exists in the vertical direction.
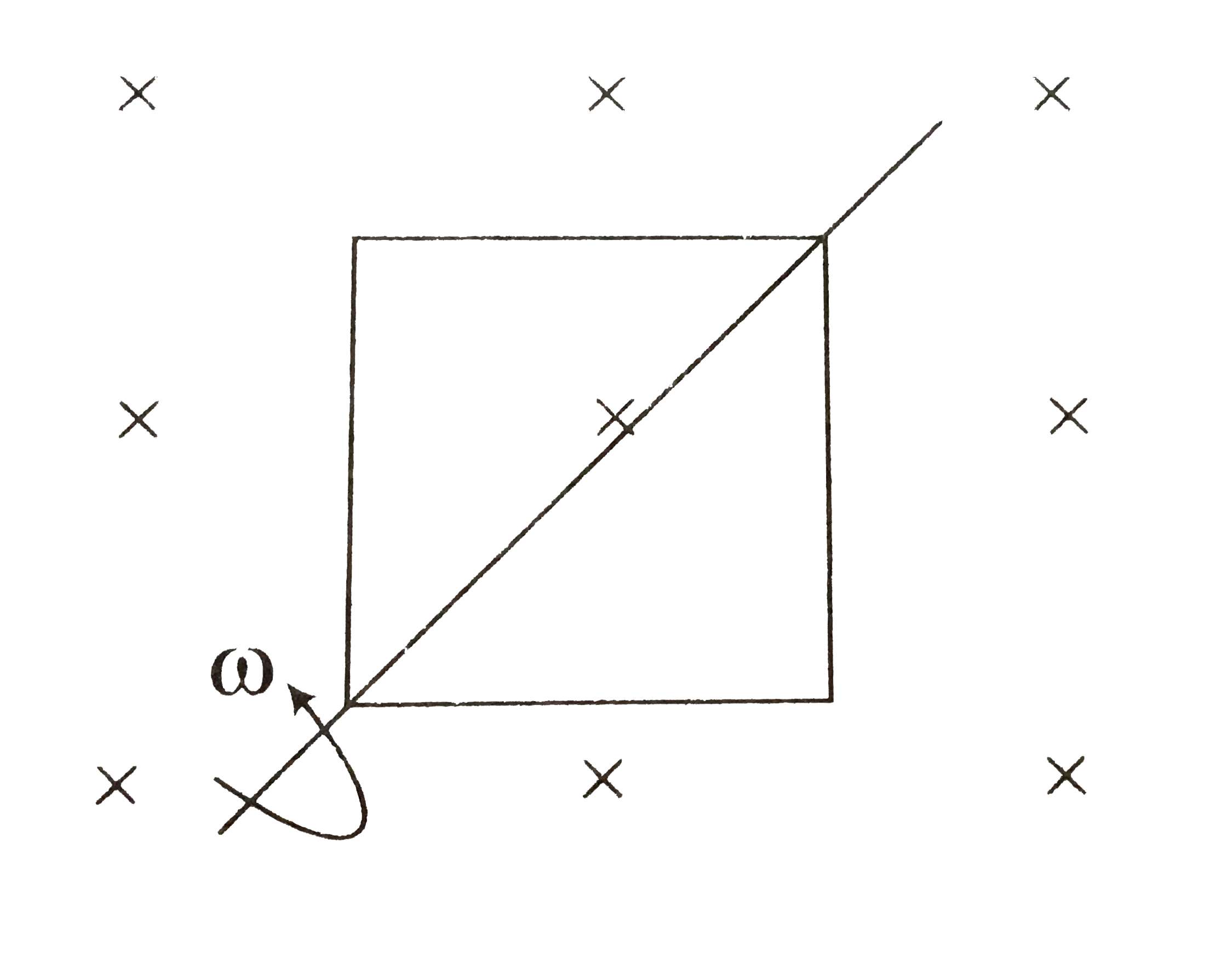
Find (i) the emf induced in the coil as a function of time t.
(ii) the maximum emf induced.
(iii) the average emf induced in the loop over a long period.
(iv) if resistance of loop is R, amount of charge flown in time t = 0 to t = 2T.
(v) heat produced in time t = 0 to t = 2T.
View SolutionA square loop of edge a having n turns Is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position . A uniform magnetic field B exists in the vertical direction. Find the emf induced in the coil.

View SolutionTwo identical coils, one of copper and the other of iron, are rotated with the same angular velocity ω in a uniform magnetic field. In which case the induced e.m.f. is more and why?
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View SolutionFor the L shaped conductor in a uniform magnetic field B shown in figure the emf across its ends when it rotates with angular velocity ω about an axis through one its ends O and normal to its plane will be
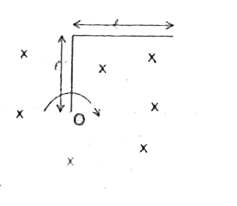
View Solution
