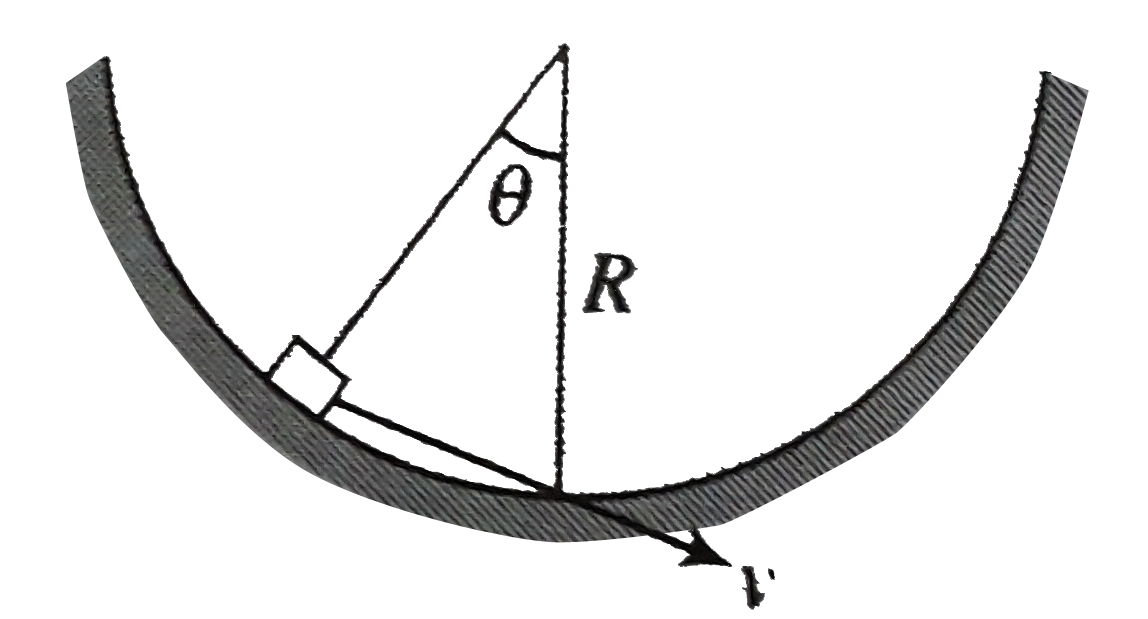
A coin is pushed down tangentially from position on a cylindrical surface with a velocity as shown in Fig. If the coefficient of friction between the coin and surface is find the tangential acceleration of the coin

As the coin slides down , friction brcause kinetic and acts up along the plane . Apart from this coin experiences and as shown in Fig
Force equation in radial direction :
…..(i)
…..(ii)
Law of kinetic friction .....(iii)
We know radius acceleration of the particle .....(iv)

Substititing Eq (iii) and from Eq (iv) in (ii) , we have
Now , Substititing from wq (i) in in Eq (v) we have
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Solved Examples
12 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Exercise 7.1
25 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A coin is pushed down tangentially from an angular position θ on a cylindrical surface , with a velocity v as shown in figure If the coefficient of friction the coin and surface is μ find the tangential acceleration of the coin
View SolutionThe coefficient of friction between two surface is μ=0.8. The tension in the string as shown in the figure is
View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA disc of radius R rotates from rest about a vertical axis with a constant angular acceleration such that a coin placed with a tangenitial between a as shown in figure If the coefficient of static friction between the coin and disc is μs .Find the velocity of the before it start sliding relative as the disc

View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If mu is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionA block B is pushed momentarily along a horizontal surface with an initial velocity v . If μ is the coefficient of sliding friction between B and the surface, block B will come to rest after a time:

View SolutionA block of mass m is slowly pulled along a curved surface from position 1 and 2. If the coefficient of kinetic friction between the block and surface is μ, find the work done by the applied force.

View SolutionA block mass m=2kg is accelerating by a force F=20N applied on a smooth light pully as shown in fig 7.86 If the coefficient of kinetic friction between the block and the surface is μ=0.3 find its acceleration

View SolutionA particle of mass m is pulled along an arbitrary curved surface without acceleration as shown in figure. Coefficient of friction between surface and particle is μ. Then


codes:
View SolutionBlock B rests on a smooth surface .The coefficient of static friction between A and B is μ=0.4 where F=30N then

Acceleration of upper block is
View Solution
