A completely inelastic collision occurs between two balls of wet putty that move directly toward cach other along a vertical axis. Just before the collision, one ball, of mass 3.0 kg, is moving upward at 20 m/s and the other ball, of mass 2.0 kg, is moving downward at 10 m/s. How high do the combined two balls of putty rise above the collision point? (Neglect air drag.)
The correct Answer is:3.3 m
To solve the problem, we will follow these steps:
Step 1: Understand the scenario
We have two balls of wet putty colliding inelastically. One ball has a mass of 3.0 kg moving upward at 20 m/s, and the other has a mass of 2.0 kg moving downward at 10 m/s. After the collision, they stick together and move with a common velocity.
Step 2: Apply the conservation of momentum
The total momentum before the collision must equal the total momentum after the collision.
Let:
- m1=3.0kg (mass of the first ball)
- u1=20m/s (velocity of the first ball)
- m2=2.0kg (mass of the second ball)
- u2=−10m/s (velocity of the second ball, negative because it is moving downward)
Using the conservation of momentum:
m1u1+m2u2=(m1+m2)v
Substituting the values:
(3.0kg⋅20m/s)+(2.0kg⋅−10m/s)=(3.0kg+2.0kg)v
60−20=5v
40=5v⟹v=405=8m/s
Step 3: Determine the maximum height reached after the collision
After the collision, the combined mass of the two balls is:
m=m1+m2=3.0kg+2.0kg=5.0kg
The initial velocity v=8m/s (upward). We will use the kinematic equation to find the maximum height h:
v2=u2+2as
Where:
- v=0m/s (final velocity at the maximum height)
- u=8m/s (initial velocity)
- a=−9.8m/s2 (acceleration due to gravity, negative because it acts downward)
- s=h (displacement, which is the height we want to find)
Substituting the values:
0=(8)2+2(−9.8)h
0=64−19.6h
19.6h=64⟹h=6419.6≈3.27m
Step 4: Conclusion
The maximum height that the combined two balls of putty rise above the collision point is approximately 3.27 meters.
---
We have two balls of wet putty colliding inelastically. One ball has a mass of 3.0 kg moving upward at 20 m/s, and the other has a mass of 2.0 kg moving downward at 10 m/s. After the collision, they stick together and move with a common velocity.
The total momentum before the collision must equal the total momentum after the collision.
- m1=3.0kg (mass of the first ball)
- u1=20m/s (velocity of the first ball)
- m2=2.0kg (mass of the second ball)
- u2=−10m/s (velocity of the second ball, negative because it is moving downward)
m1u1+m2u2=(m1+m2)v
Substituting the values:
(3.0kg⋅20m/s)+(2.0kg⋅−10m/s)=(3.0kg+2.0kg)v
60−20=5v
40=5v⟹v=405=8m/s
After the collision, the combined mass of the two balls is:
m=m1+m2=3.0kg+2.0kg=5.0kg
The initial velocity v=8m/s (upward). We will use the kinematic equation to find the maximum height h:
v2=u2+2as
Where:
- v=0m/s (final velocity at the maximum height)
- u=8m/s (initial velocity)
- a=−9.8m/s2 (acceleration due to gravity, negative because it acts downward)
- s=h (displacement, which is the height we want to find)
0=(8)2+2(−9.8)h
0=64−19.6h
19.6h=64⟹h=6419.6≈3.27m
The maximum height that the combined two balls of putty rise above the collision point is approximately 3.27 meters.
Topper's Solved these Questions
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Single Correct Choice )47videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)5videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Integer )4videos
CENTER OF MASS
- BOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)3videos
CAPACITANCE
- BOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)3videos
CIRCUITS
Similar Questions
A ball of mass 1kg moving with 4m−1 along +x-axis collides elastically with an another ball of mass 2kg moving with 6m/s is opposite direction. Find their velocities after collision.
View SolutionA ball of mass 100g moving at a speed of 12 m s−1 strikes another ball of mass 200 g at rest. After the collision both the balls move with a common velocity. Find the common velocity.
View Solution
Knowledge Check
- Question 1 - Select One
A completely inelastic collision occurs between two balls of wet putty that move directly toward each other along a vertical axis. Just before the collision, one ball, of mass 3.0 kg, is moving upward at 20 m/s and the other ball, of mass 2.0 kg, is moving downward at 12 m/s. How high do the combined two balls of putty rise above the collision point? (Neglect air drag.)
A2.3 mB2.0 mC2.6 mD2.9 m - Question 2 - Select One
A ball of mass 10 kg is moving with a velocity of 10 m / s . It strikes another ball of mass 5 kg which is moving in the same direction with a velocity of 4 m / s . If the collision is elastic, their velocities after the collision will be, respectively
A6m/s, 12m/sB12m/s, 6m/sC12 m/s, 10 m/sD12m/s, 25m/s - Question 3 - Select One
A metal ball of mass 2 kg moving with a velocity of 36km/h has a head on collision with a stationery ball of mass 3 kg. If after the collision, the two balls move together, the loss in kinetic energy dur to collision is
A140JB100JC60JD40J
A ball of mass 5 kg moving velocity 3m/s impinges direction on another ball of mass 2 kg moving with velocity 0.5m/s towards the first ball. Find the velocity after impact, if e=47
View SolutionA ball of mass 100g moving at a speed of 12 m s−1 strikes another ball of mass 200 g at rest. After the collision both the balls move with a common velocity. Find the common velocity.
View SolutionTwo balls are moving towards each other on a vertical line collides with each other as shown. Find their velocities just after collision.
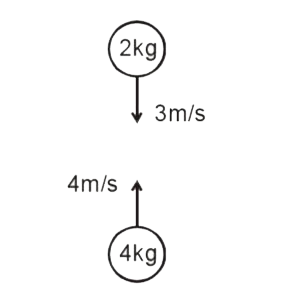 View Solution
View SolutionA ball of mass 0.50 kg moving at a speed of 5.0 m/s collides with another ball of mas 1.0 kg. After the collision the balls stick together ane remain motionless. What was the velocity of the 1.0 kg block before the collision?
View SolutionA body of mass 2kg moving with a velocity 3m/s collides with a body of mass 1kg moving with a velocity of 4m/s in opposite direction. If the collision is head on and completely inelastic, then
View Solution

