A conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1mms−1. The induced emf when the radius is 2cm is
2πμV
πμV
π2μV
2μV
The correct Answer is:B
To solve the problem step by step, we will calculate the induced EMF in the conducting circular loop based on the given parameters.
Step 1: Identify the given values
- Magnetic field strength, B=0.025T
- Rate of change of radius, drdt=−1mm/s=−1×10−3m/s (negative because the radius is shrinking)
- Radius of the loop at the moment of interest, r=2cm=2×10−2m
Step 2: Calculate the magnetic flux Φ
The magnetic flux through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
Since the plane of the loop is perpendicular to the magnetic field, θ=0∘ and cos(0)=1. The area A of the circular loop is:
A=πr2
Thus, the magnetic flux becomes:
Φ=B⋅πr2
Step 3: Differentiate the magnetic flux to find induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Substituting the expression for magnetic flux:
E=−ddt(B⋅πr2)
Since B is constant, we can take it out of the differentiation:
E=−B⋅πddt(r2)
Using the chain rule:
ddt(r2)=2rdrdt
Thus, the induced EMF becomes:
E=−B⋅π⋅2rdrdt
Step 4: Substitute the known values
Now, substituting the known values into the equation:
E=−0.025⋅π⋅2⋅(2×10−2)⋅(−1×10−3)
Calculating this step-by-step:
1. Calculate 2⋅(2×10−2)=4×10−2
2. Now substitute:
E=0.025⋅π⋅(4×10−2)⋅(1×10−3)
3. Simplifying further:
E=0.025⋅π⋅4×10−5
4. Calculate 0.025⋅4=0.1:
E=0.1⋅π×10−5
5. Therefore:
E=π×10−6V
Final Result
The induced EMF when the radius is 2 cm is:
E=π×10−6V(or μV)
- Magnetic field strength, B=0.025T
- Rate of change of radius, drdt=−1mm/s=−1×10−3m/s (negative because the radius is shrinking)
- Radius of the loop at the moment of interest, r=2cm=2×10−2m
The magnetic flux through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
Since the plane of the loop is perpendicular to the magnetic field, θ=0∘ and cos(0)=1. The area A of the circular loop is:
A=πr2
Thus, the magnetic flux becomes:
Φ=B⋅πr2
According to Faraday's law of electromagnetic induction, the induced EMF E is given by:
E=−dΦdt
Substituting the expression for magnetic flux:
E=−ddt(B⋅πr2)
Since B is constant, we can take it out of the differentiation:
E=−B⋅πddt(r2)
Using the chain rule:
ddt(r2)=2rdrdt
Thus, the induced EMF becomes:
E=−B⋅π⋅2rdrdt
Now, substituting the known values into the equation:
E=−0.025⋅π⋅2⋅(2×10−2)⋅(−1×10−3)
Calculating this step-by-step:
1. Calculate 2⋅(2×10−2)=4×10−2
2. Now substitute:
E=0.025⋅π⋅(4×10−2)⋅(1×10−3)
3. Simplifying further:
E=0.025⋅π⋅4×10−5
4. Calculate 0.025⋅4=0.1:
E=0.1⋅π×10−5
5. Therefore:
E=π×10−6V
The induced EMF when the radius is 2 cm is:
E=π×10−6V(or μV)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXEMPLAR PROBLEMS
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - ASSERTION AND REASON
15 Videos
- ELECTRIC CHARGES AND FIELDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Assertion And Reason
15 Videos
- ELECTROMAGNETIC WAVESBOOK - NCERT FINGERTPS ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Assertion And Reason
15 Videos
Similar Questions
A conducting circualr loop is placed in a unifrom magentic field , B= 0.025 T with its plane perpendicular to the loop .The radius of the loop is made to shrink at a constant rate of 1 mms−1 .The induced emf when the radius is 2cm ,is
View SolutionA conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View SolutionA conducting circular loop is placed in a uniform magnetic field 0.04T with its plane perpendicular to the magnetic field. The radius of the loop starts shrinking at 2mm/sec . The induced emf in the loop when the radius is 2cm is:
(1.) 3.2 π μ V
(2.) 4.8 π μ V
(3.) 0.8 π μ V
(4.) 1.6 π μ V
View SolutionA rectangular copper coil is placed in a uniform magnetic field of induction 40 mT with its plane perpendicular to the field. The area of the coil is shrinking at a constant rate of 0.5m2s−1. The emf induced in the coil is
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View SolutionA conducing circular loop is placed in a uniform magnetic field of indution B tesla with its plane normal to the field. Now, radius of the loop starts shrinking at the rate (dr/dt). Then the induced e.m.f. at the instant when the radius is r is:
View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View SolutionA metallic loop is placed in a non-uniform steady magnetic field. Will an emf be induced in the loop?
View SolutionA conducting loop carrying a current I is placed in a uniform magnetic field ponting into the plane of the paper as shown. The loop will have a tendency to
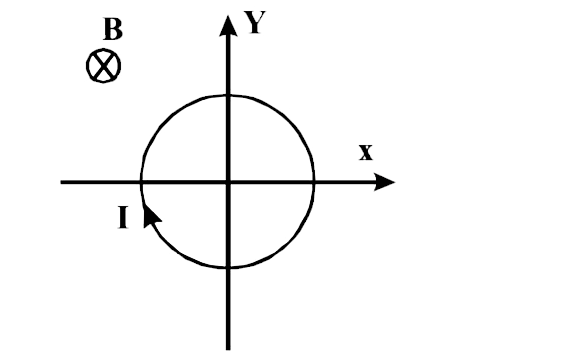
View SolutionA semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
View Solution
