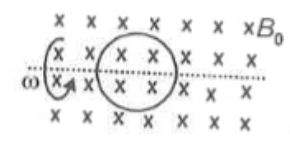
A semi-circular loop of radius R is placed in a uniform magnetic field as shown. It is pulled with a constant velocity. The induced emf in the loop is
Bv(πR)cosθ
Br(πR)sinθ
Bv(2R)cosθ
Bv(2R)sinθ
The correct Answer is:D
To find the induced emf in a semi-circular loop of radius R that is being pulled with a constant velocity in a uniform magnetic field, we can follow these steps:
1. Identify the Parameters:
- Let the radius of the semi-circular loop be R.
- Let the uniform magnetic field be B.
- Let the constant velocity with which the loop is pulled be V.
2. Understand the Geometry:
- The semi-circular loop has a diameter 2R.
- As the loop is pulled, only the segment of the loop that is moving through the magnetic field will contribute to the induced emf.
3. Determine the Effective Length:
- The effective length L of the segment of the loop that is moving through the magnetic field is equal to the diameter of the semi-circle, which is L=2R.
4. Calculate the Induced EMF:
- According to Faraday's law of electromagnetic induction, the induced emf ϵ in a circuit is given by the formula:
\epsilon = B \cdot V_{\perpendicular} \cdot L
- Here, V_{\perpendicular} is the component of the velocity perpendicular to the magnetic field. If the magnetic field is uniform and directed in a specific direction, we can express this as:
V_{\perpendicular} = V \cdot \sin(\theta)
- Therefore, substituting V_{\perpendicular} into the emf equation gives:
ϵ=B⋅(V⋅sin(θ))⋅(2R)
5. Final Expression for Induced EMF:
- Thus, the induced emf in the semi-circular loop can be expressed as:
ϵ=B⋅V⋅2R⋅sin(θ)
Conclusion:
The induced emf in the semi-circular loop being pulled in a uniform magnetic field is given by:
ϵ=B⋅V⋅2R⋅sin(θ)
- Let the radius of the semi-circular loop be R.
- Let the uniform magnetic field be B.
- Let the constant velocity with which the loop is pulled be V.
- The semi-circular loop has a diameter 2R.
- As the loop is pulled, only the segment of the loop that is moving through the magnetic field will contribute to the induced emf.
- The effective length L of the segment of the loop that is moving through the magnetic field is equal to the diameter of the semi-circle, which is L=2R.
- According to Faraday's law of electromagnetic induction, the induced emf ϵ in a circuit is given by the formula:
\epsilon = B \cdot V_{\perpendicular} \cdot L
- Here, V_{\perpendicular} is the component of the velocity perpendicular to the magnetic field. If the magnetic field is uniform and directed in a specific direction, we can express this as:
V_{\perpendicular} = V \cdot \sin(\theta)
- Therefore, substituting V_{\perpendicular} into the emf equation gives:
ϵ=B⋅(V⋅sin(θ))⋅(2R)
- Thus, the induced emf in the semi-circular loop can be expressed as:
ϵ=B⋅V⋅2R⋅sin(θ)
The induced emf in the semi-circular loop being pulled in a uniform magnetic field is given by:
ϵ=B⋅V⋅2R⋅sin(θ)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - D)
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - A)
55 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
A current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View SolutionA circular loop of radius 'a' is rotated in a uniform magnetic field B, with constant angular velocity o about diameter as shown in the figure. Choose the correct graph of induced emf & versus time t. (consider at t = 0 area vector of loop is in the direction of magnetic field)
View Solution
Knowledge Check
A conducting circular loop is placed in a uniform magnetic field, B=0.025T with its plane perpendicular to the loop. The radius of the loop is made to shrink at a constant rate of 1mms−1. The induced emf when the radius is 2cm is
A2πμVBπμVCπ2μVD2μV
A semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
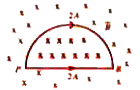
View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionA circular flexible loop of wire of radius r carrying a current I is placed in a uniform magnetic field B . If B is doubled, then tension in the loop
View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionA circular loop of radius R=20 cm is placed in a uniform magnetic field B=2T in xy-plane as shown in figure. The loop carries a current i=1.0A in the direction shown in figure. Find the magnitude of torque acting on the loop.

View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionA circular wire loop of radius r is placed in a region of uniform magnetic field B such that the plane of the loop makes an angle θ with the direction of B. In which of the following conditions, will no emf be induced in the loop?
View Solution
