A conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.Solution in Gujrati
Velocity at a dostance (r2) from the centre<br>= (r omega)/2<br>E=Blv=Bxxrxx(r omega)/2<br>=(1/2)Br^2 omega.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - EXERCISE
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMACHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 2
10 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMACHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Exercises
75 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMACHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercises
9 Videos
Similar Questions
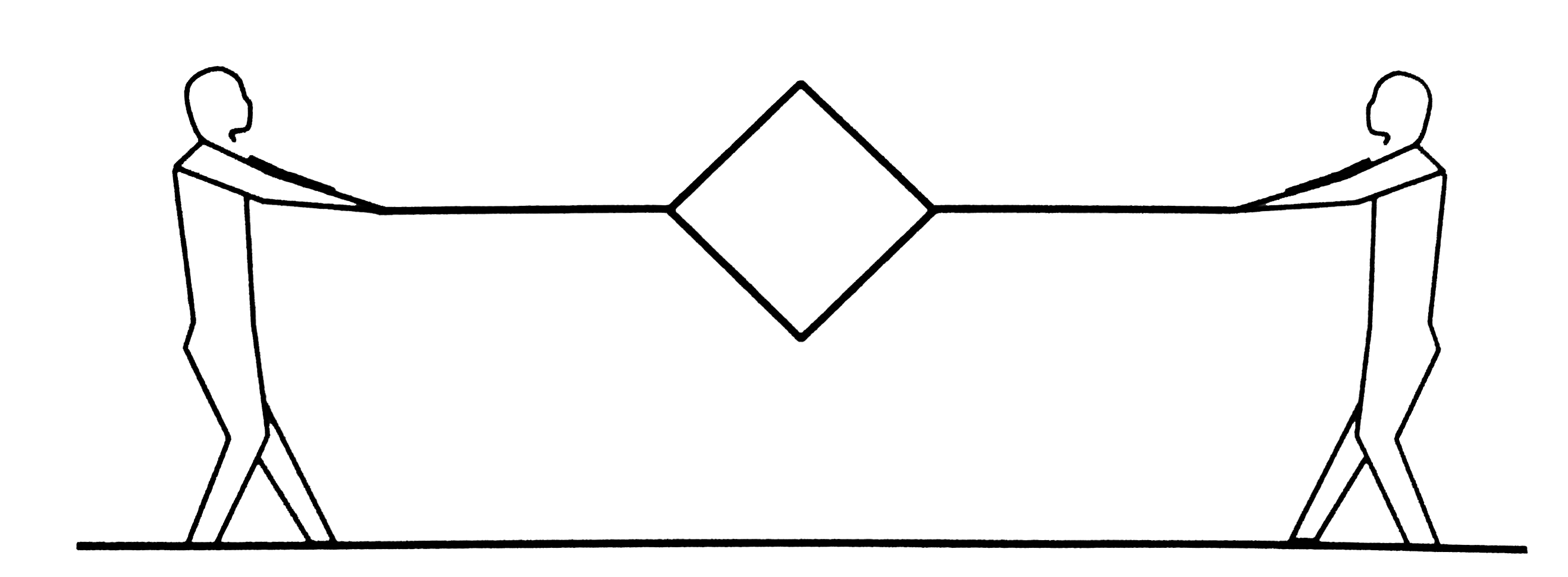
Shown a metallic square frame of edga a in a vertical plane. A uniform magnetic field B exists in the space in a directon perpendicular to the plane of the figure. Two boys pull the opposite corners of the square ot deform it into a rhombus. They start pulling the corners t t=0 and sisplace the corners at a uniform speed u. (a) find the induced emf in the frame at the instant when the angles at these corners reduce to 60∘. (b) find the induced current in the frame at this instatnt if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
View SolutionA bar magnet is moved along the axis of a copper ring placed far away from the magnet. Looking from the side of the magnet, an anticlockwise current is found to be induced in the ring. Which of the following may be true?
View SolutionFind the dimensional formula of ε0 .
View SolutionShow that the dimensions of the displacement current (ε0dΦEdt) are that of an electric current.
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA conducting disc of radius r rotates with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View SolutionA metal disc of radius R = 25 cm rotates with a constant angular velocity omega = 130 rad s^(-1) about its axis. Find the potential difference between the center and rim of the disc if (a) the external magnetic field is absent, (b) the external uniform megnetic field B = 5.0 mT directed perpendicular to the disc.
View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density sigma rotates about its axis with an angular velocity omega . Find : (a) the magnetic induction at the centre of the disc, (b) the magnetic moment of the disc. ( c) the ratio of magnetic moment and angular momentum of disc.
View Solutiona conducting disc of radius R roatates about its axis when an angular velocity omega .Then the potential difference between the centre of the disc and its edge is (no magnetic field is present ):
View SolutionA non-conducting disk of radius R is rotating about its own axis with constant angular velocity omega in a perpendicular uniform magnetic field B as shown in figure. The emf induced between centre and rim of disk is
View SolutionA non-conducting disc having unifrom positive charge Q , is rotating about its axis with unifrom angular velocity omega .The magnetic field at the centre of the disc is.
View SolutionFigure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed ω=40rad/s,B=0.10T and R=1Ω. The current through the resistor is
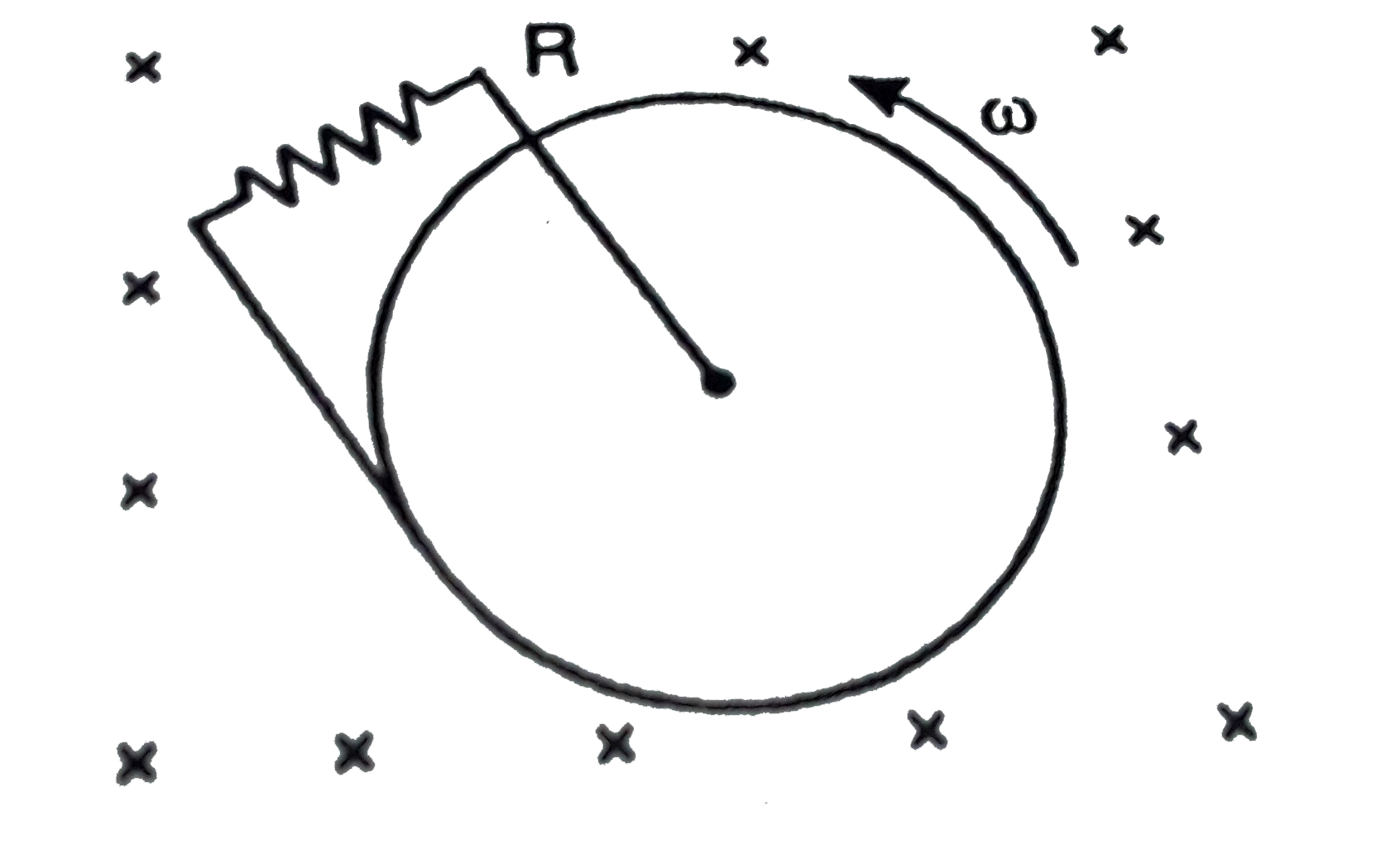
View SolutionA rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionFind the ratio of magnetic dipole moment and magnetic field at the centre of a disc. Radius of disc is R and it is rotating at constant angular speed o about its axis. The disc is insulating and uniformly charged
View Solution
