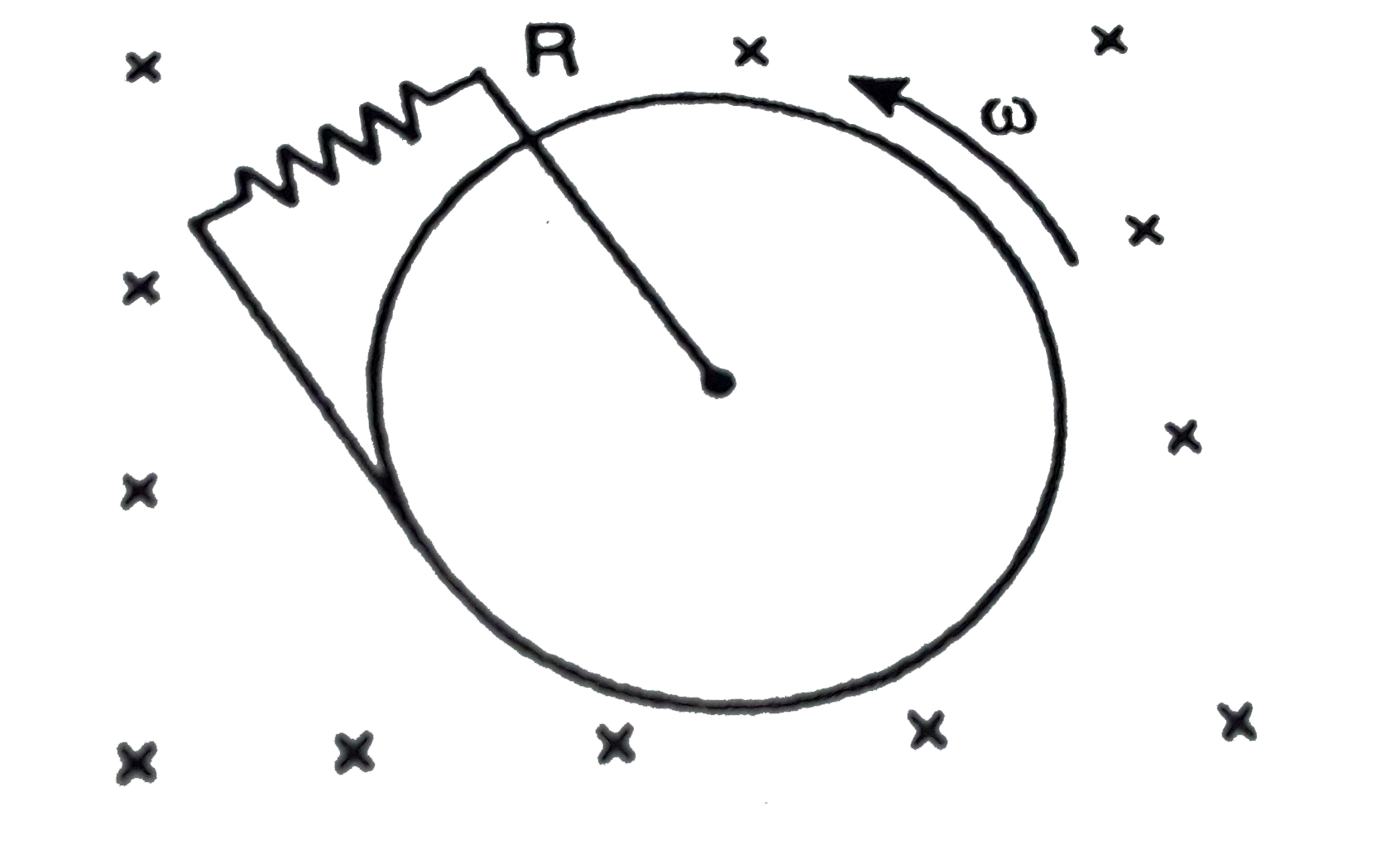
Figure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed . The current through the resistor is
5mA
50A
5A
10mA
The correct Answer is:A
Step by step video & image solution for Figure shows a conducting disc rotating about its axis in a perpendicular uniform and constant magnetic field B. A resistor of resistance R is connected between the centre and the rim. The radius of the disc is 5.0 cm, angular speed omega=40 rad//s, B=0.10 T " and " R=1 Omega. The current through the resistor is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
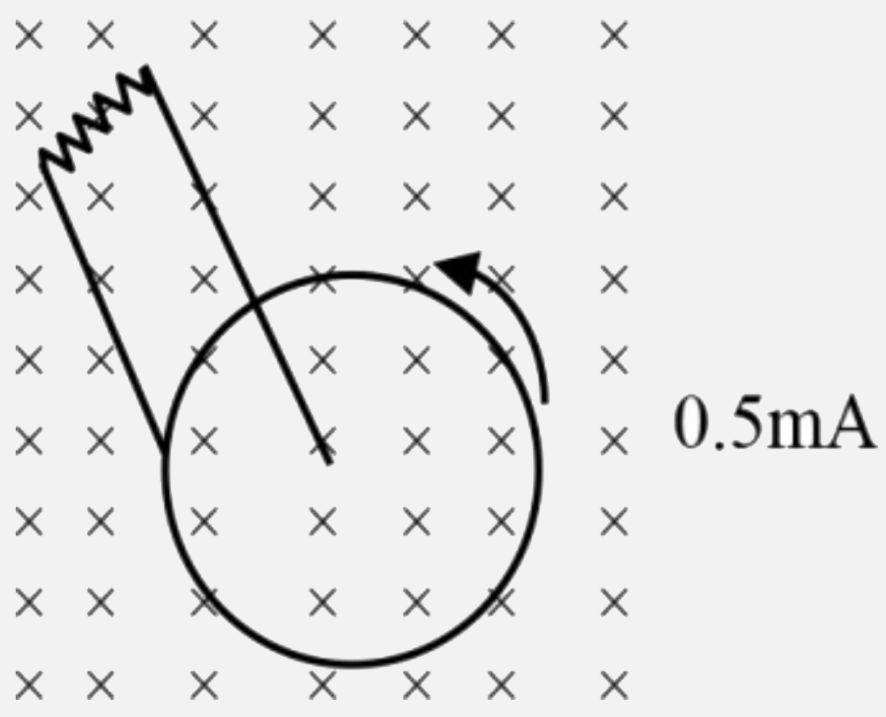
The following figure a conducting disc rotating about its axis in a perpendicular magnetic field B. The resistor of resistance R is connected between the centre and the rim. The current in the resistor is (The radius of the disc is 5.0 cn=m, angular speed ω=10rads−1,B=0.40TandR=10Ω)
View SolutionA copper disc of radius 0.1 m is rotated about its natural axis with 10 rps in a uniform magnetic field of 0.1 T with its plane perpendicular to the field, The emf induced across the radius of the disc is
View SolutionA conducting disc of radius r rotaes with a small but constant angular velocity ω about its axis. A uniform magnetic field B exists parallel to the axis of rotation. Find the motional emf between the centre and the periphery of the disc.
View SolutionA metallic rod of length l is rotated at a constant angular speed ω, normal to a uniform magnetic field B. Derive an expression for the current induced in the rod, if the resistance of the rod is R.
View SolutionA non-conducting disc having unifrom positive charge Q, is rotating about its axis with unifrom angular velocity ω.The magnetic field at the centre of the disc is.

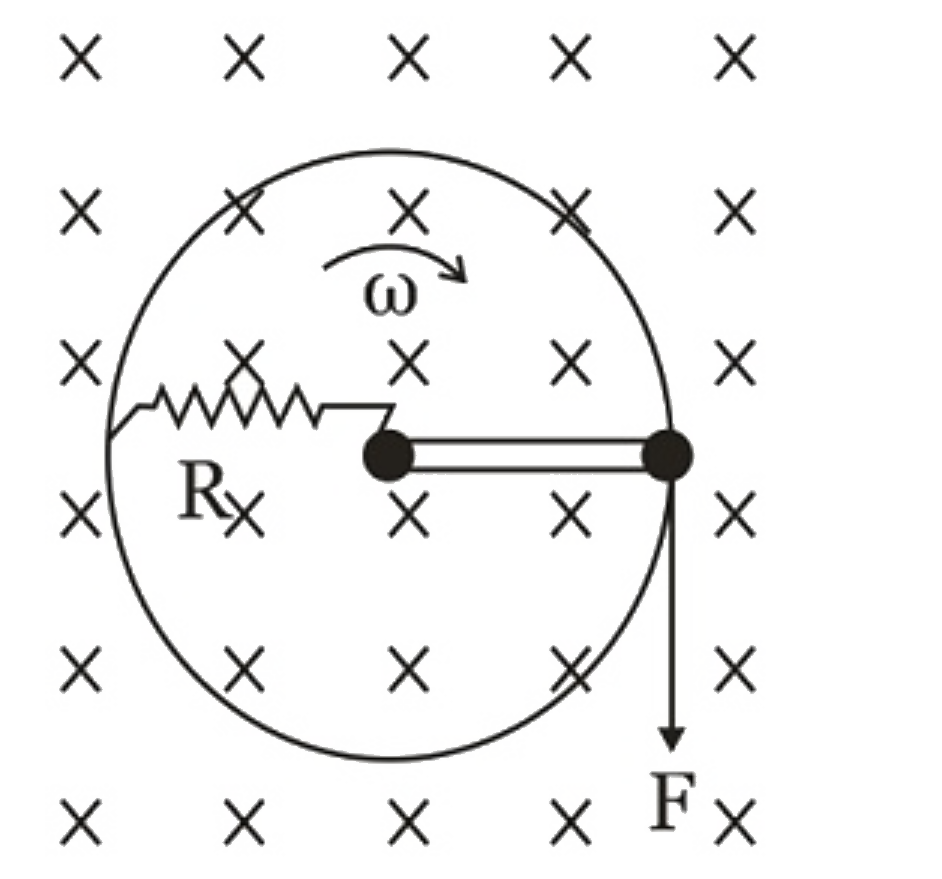
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)

View SolutionA conducting disc of radius R is placed in a uniform and constant magnetic field B parallel to the axis of the disc.With what angular speed should the disc be rotated about its axis such that no electric field develops in the disc (the electric charge and mass are e and m)
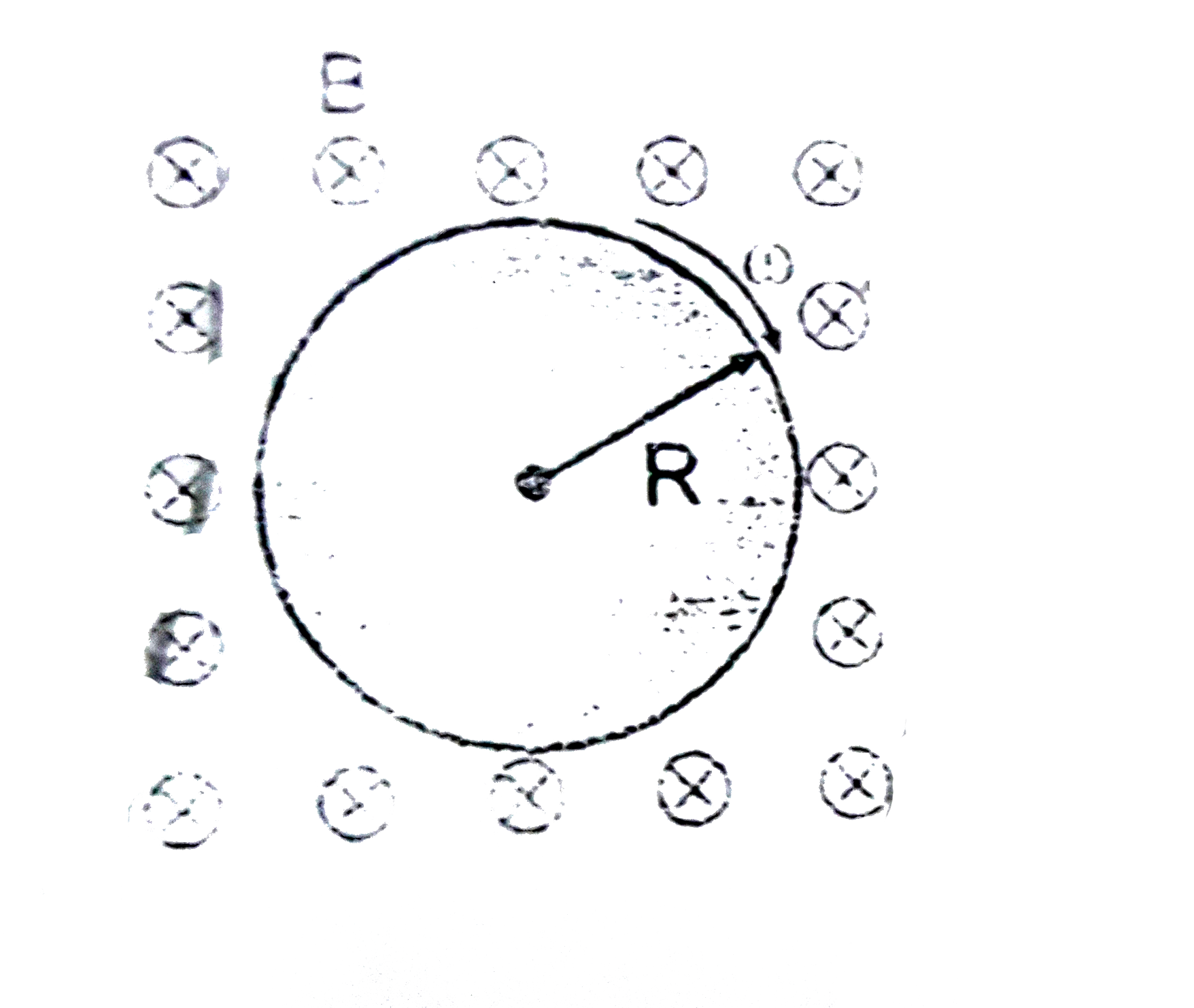
View SolutionA metallic ring of mass 2 kg and radius 1 m with with a uniform metallic spoke of same mass 2 kg and length 1 m is rotated about its axis with angular velocity 1 rev sec−1. In a perpendicular uniform magnetic field B of magnitude 10 T as shown in the figure. If the central end of the spoke is connected to the rim of the wheel through a resistor R of magnitude πΩ as shown. The resistor does not rotate, It's one end is always at the centre of the ring and another end is always in contact with the ring. A force F as shown is needed to maintain the constant angular velocity of the spoke then, F is equal to (The ring and the spoke has zero resistance)
View SolutionShows a conducting circular loop radius a placed in a uniform, perpendicular magnetic field B. A metal rod OA is pivoted at the centre O of the loop. The other A of the rod touches the loop. The rod OA and the loop are resistanceless but a resistor having a resistance R is connected between O and a fixed point C on the loop . the rod OA is made to rotate anticlockwise at a small but uniform angular speed omega by an external force. Find (a) the current in the resistance R and (b) the torque of the external force needed ot keep the rod rotating with the constant angular velocity omega.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View Solution
