A conductor of orbitrary shape, carrying a charge , is surrounded with uniform dielectric of permittivity (Fig).

Find the total bound charges at the inner and outer surfaces of the dilectric.
From the solution of the previous problem = charge on the inerior surface of the conductor
on the outer surface of the dielectric.
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Current72videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Motion Of Charged Particle In Magnetic Field36videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
Initially the space between the plates of the capacitor is filled with air, and the field strength in the gap is equal to E0. Then half the gap is filled with uniform isotropic dielectric with permittivity ε as shown in Fig. Find the moduli of the introduction of the dielectric
(a) deos not change the voltage across the plates,
(b) leaves the charges at the plates constant.
 View Solution
View SolutionHalf the space between two concentricv elecrodes of a sphereical capacitor is filled , as shwon in Fig, with unifrom istropic dielectric with permittively ε. The charge of the capacitor is q. Find the magnitude of the electric field strength between teh electrodes as a function of distance r from the curvature centre of teh electrodes.
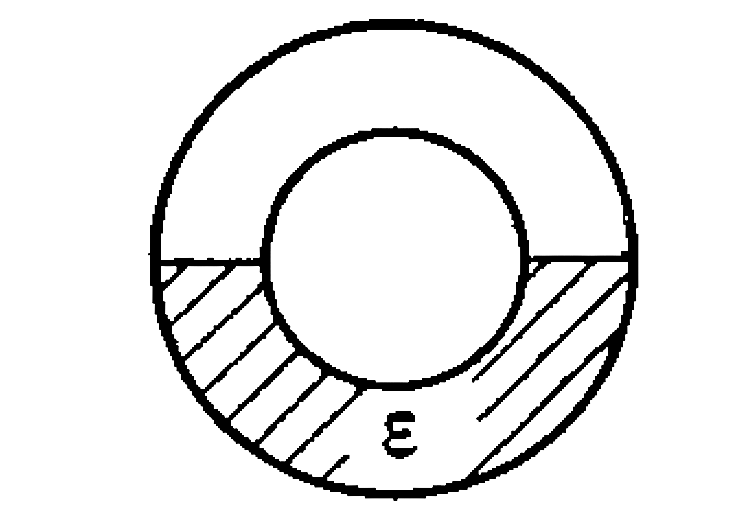 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the given diagram, there is a conducting sphere of radius r which is surrounded by a dielectric of relative permittivity εr. If conducting sphere is given charge q, then surface density of polarization charges, on the outer surface of the dielectric layer, is
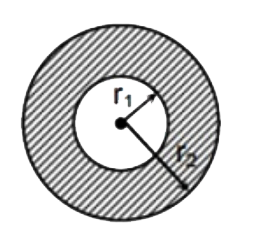 Aεrq4πr22Bq4πεrr22C(εr−1)q4πr22D(εr−1)q4πεrr22
Aεrq4πr22Bq4πεrr22C(εr−1)q4πr22D(εr−1)q4πεrr22 - Question 2 - Select One
Find the total flux due to charge qassociated with the given hemisphercal surface
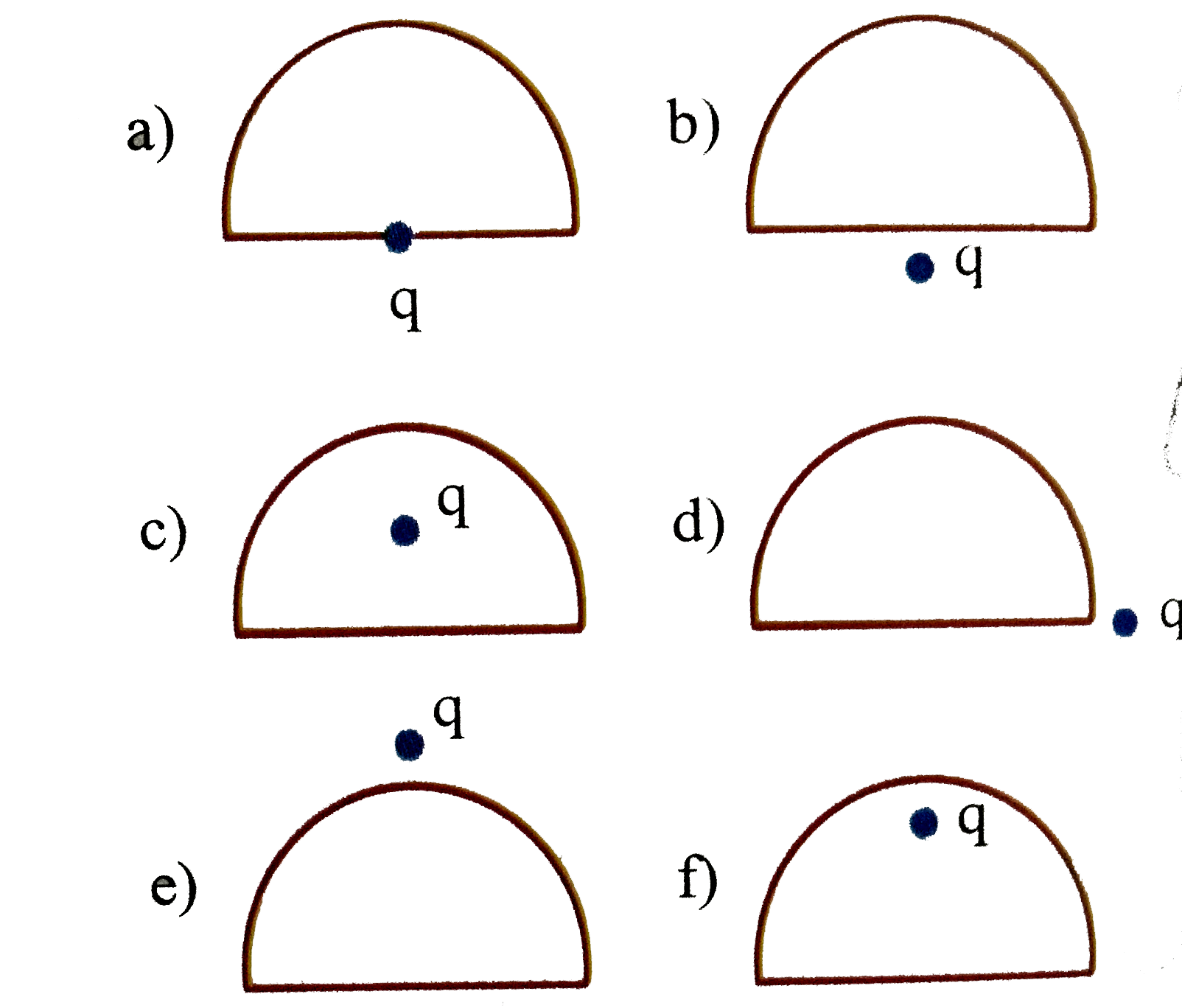 Aq2ε0,(b)0,(c)qε0,(d)0,(e)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0C(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0D(a)0,(b)q2ε0,(c)0,(d)qε0,(e)qε0(f)qε0
Aq2ε0,(b)0,(c)qε0,(d)0,(e)qε0B(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0C(a)0,(b)q2ε0,(c)0,(d)qε0,(e)0,(f)qε0D(a)0,(b)q2ε0,(c)0,(d)qε0,(e)qε0(f)qε0 - Question 3 - Select One
A conducting sphere that carries a total charge of -3q is placed at the centre of a conducting spherical shell that carries a total charged of +5q. The conductors are in electrostatic equilibrium. The charges on the inner and outer surfaces of the shell are respectively.
 A+3q,+2qB+q,+qC+2q,+3qD+2q,+7q
A+3q,+2qB+q,+qC+2q,+3qD+2q,+7q
A point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
A charge q is placed at the centre of the shell. Find out the surface charge density on the inner and outer surface of the shell.
Is the electric field inside a cavity (with no charge ) zero. Independent of the fact wheather the shell is spherical or not ? Explain.View SolutionA point charge q is located at the centre of a ball made of uniform istopic dielectric with permittivity epsilon. Find the polarizaion P as a function of the radius vector r relative to the centre of the system, as well as the chagre q' inside a sphere whose radius is less than radius of the ball.
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q:
(a) A charge q is placed at the centre of the shell. What is the surface charge density on the inner and outer surfaces of the shell?
(b) Is the electric field inside a cavity (with no charge) zero even if the shell is not spherical, but has any irregular shape? Explain.View Solution

