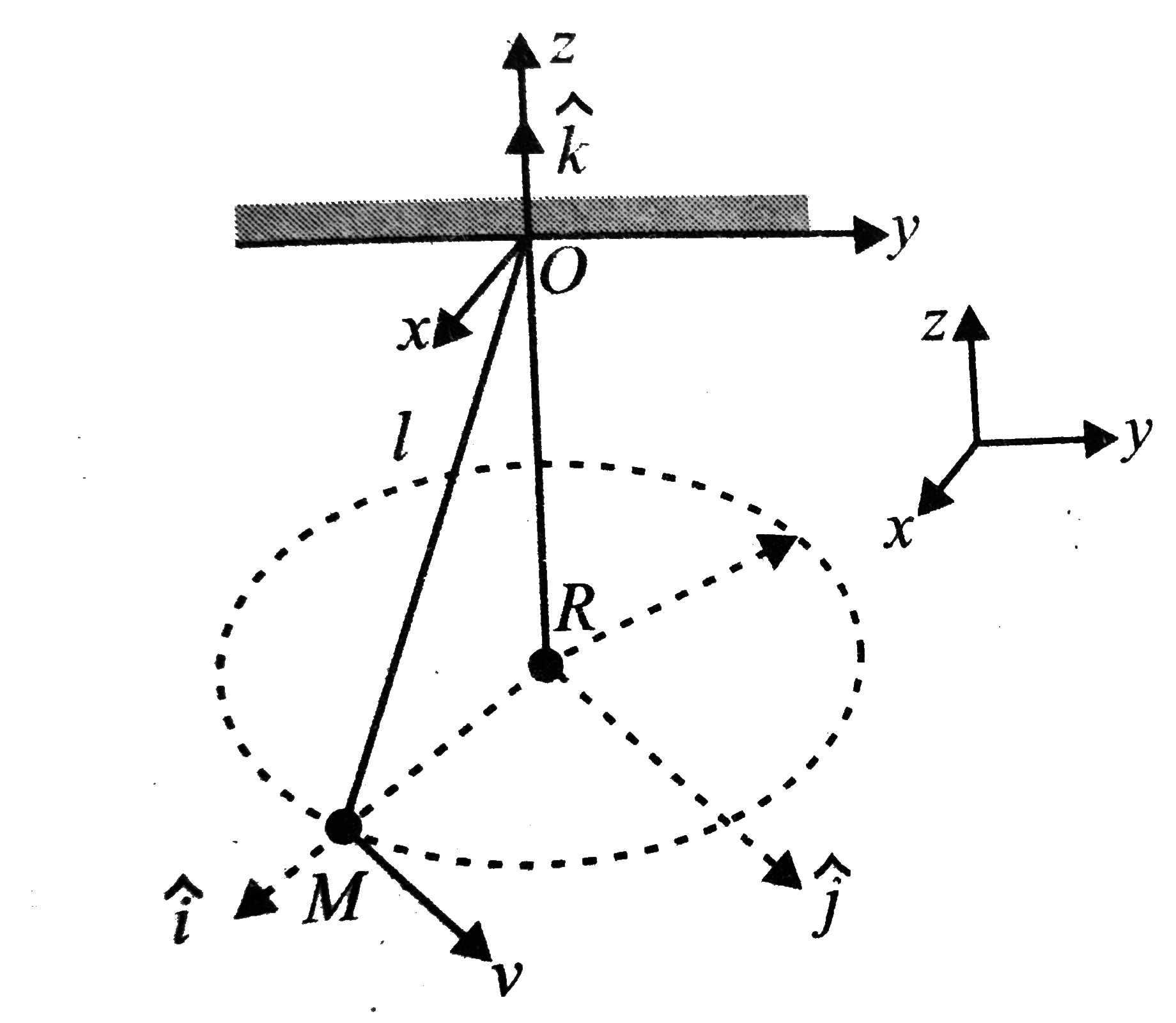
A conical pendulum consists of a mass M suspended from a strong sling of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and vˆj velocity. At time t the angular momentum vector of mass M about the point from which the string passes on the ceiling is
MvRˆk
Mvlˆk
Mvl[√l2−R2lˆi+Rlˆk]
−Mvl[√l2−R2lˆi+Rlˆk]
The correct Answer is:C
From the figure in questions position vector if mass →r=Rˆi−√l2+R3ˆk
Linear moment →p=Mvˆj
→L=→v×→p
substituting the values, we get result
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
Consider a conical pendulum having bob is mass m is suspended from a ceiling through a string of length L. The bob moves in a horizontal circle of radius r. Find (a) the angular speed of the bob and (b) the tension in the string.

View SolutionA particle of mass m is suspended from a ceiling through a string of length L. The particle moves in a horizontal circle of radius r such that r =L√2. The speed of particle will be :
View Solution
Knowledge Check
A conical pendulum consists of a mass M suspended from a string of length l. The mass executes a circle of radius R in a horizontal plane with speed v. At time t, the mass is at position Rˆi and has velocity vˆj. At time t, the angular momentum vector of the mass M about the point from which the string suspended is
 AMυRˆkBmυlˆkCMυl[(√l2−R2lˆi)+Rlˆk]D−Mυl[(√l2−R2lˆi)+Rlˆk]
AMυRˆkBmυlˆkCMυl[(√l2−R2lˆi)+Rlˆk]D−Mυl[(√l2−R2lˆi)+Rlˆk]A particle of mass m is suspended from the ceiling through a string of length L. The particle moves in a horizontal circle of radius r. The speed of the particle is
Arg√L2−r2Br√g(L2−r2)14Cr√g(L2−r2)12DmgL(L2−r2)12A particle of mass ma is suspended from a ceiling thrugh a string of length L. The prticle moves in a horizontal circle of radius r. Find (a) the speed of the prticle and (b). the tension in the string. Sch a system is called a conical pendulum
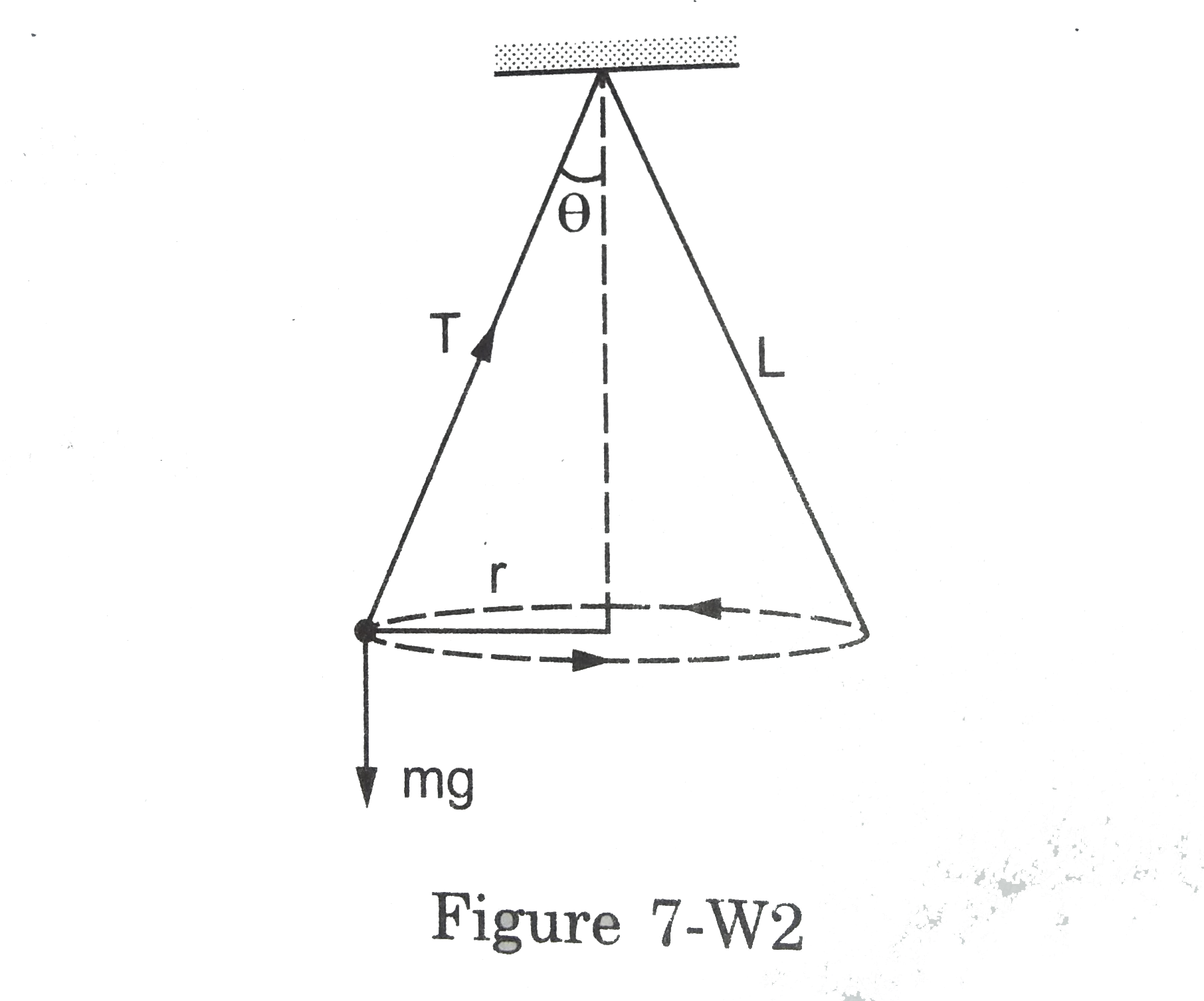
.Av=r√g(L2−r2)14andT=mgL(L2−r2)12Bv=r2√g(L3−r3)14andT=mgL(L2−r2)12Cv=r√g(L2−r2)14andT=mgL2(L2−r2)12Dv=r√g(L2−r2)14andT=mgL(L2−r2)14
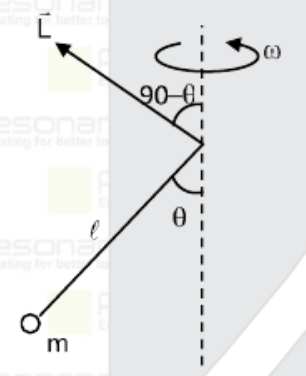
A bob of mass m attached to an inextensible string of length l, is suspended from a vertical support. Bob rotates in a horizontal circle with angular speed ω and string makes an angle of θ with the vertical. Find the angular momentum of bob about axis of rotation
View SolutionFind the angular momentum of a particle of mass m describing a circle of radius r with angular speed ω.
View SolutionA particle of mass m is tied to a string of length L and whirled into a horizontal plan. If tension in the string is T then the speed of the particle will be :
View SolutionA particle of mass m is moving along a circle of radius r with a time period T. Its angular momentum is
View SolutionA paricle of mass m is tied to a light string of length L and moving in a horizontal circle of radius r with speed v as shown. The forces acting on the particle are

View Solution