A constant power P is applied on a particle of mass m. find kintic energy, velocity and displacement of particle as function of time t.
The correct Answer is:B, C
To solve the problem of finding the kinetic energy, velocity, and displacement of a particle of mass m under the influence of a constant power P, we can follow these steps:
Step 1: Relate Power to Work Done
We know that power P is defined as the rate of doing work, which can be expressed mathematically as:
P=Wt
where W is the work done and t is the time. Rearranging this gives us:
W=P⋅t
Step 2: Relate Work Done to Change in Kinetic Energy
The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy. Thus:
W=ΔKE=KE−KE0
Assuming the particle starts from rest, KE0=0, we have:
ΔKE=KE=W
Substituting the expression for work done, we get:
KE=P⋅t
Step 3: Express Kinetic Energy in Terms of Velocity
The kinetic energy of a particle is given by:
KE=12mv2
Setting this equal to the expression we found for kinetic energy:
12mv2=P⋅t
Step 4: Solve for Velocity
Now, we can solve for the velocity v:
mv2=2Pt
v2=2Ptm
Taking the square root gives:
v=√2Ptm
Step 5: Express Velocity as a Function of Time
We can rewrite the expression for velocity:
v=√2Pm⋅t1/2
Step 6: Find Displacement as a Function of Time
To find displacement s, we use the relationship:
v=dsdt
This implies:
ds=v⋅dt
Substituting the expression for v:
ds=√2Pm⋅t1/2⋅dt
Integrating both sides gives:
s=∫√2Pm⋅t1/2dt
The integral of t1/2 is:
∫t1/2dt=23t3/2
Thus, we have:
s=√2Pm⋅23t3/2+C
Assuming the initial displacement is zero (i.e., C=0):
s=23√2Pmt3/2
Final Results
1. Kinetic Energy:
KE=P⋅t
2. Velocity:
v=√2Pm⋅t1/2
3. Displacement:
s=23√2Pmt3/2
We know that power P is defined as the rate of doing work, which can be expressed mathematically as:
P=Wt
where W is the work done and t is the time. Rearranging this gives us:
W=P⋅t
The work-energy theorem states that the work done on an object is equal to the change in its kinetic energy. Thus:
W=ΔKE=KE−KE0
Assuming the particle starts from rest, KE0=0, we have:
ΔKE=KE=W
Substituting the expression for work done, we get:
KE=P⋅t
The kinetic energy of a particle is given by:
KE=12mv2
Setting this equal to the expression we found for kinetic energy:
12mv2=P⋅t
Now, we can solve for the velocity v:
mv2=2Pt
v2=2Ptm
Taking the square root gives:
v=√2Ptm
We can rewrite the expression for velocity:
v=√2Pm⋅t1/2
To find displacement s, we use the relationship:
v=dsdt
This implies:
ds=v⋅dt
Substituting the expression for v:
ds=√2Pm⋅t1/2⋅dt
Integrating both sides gives:
s=∫√2Pm⋅t1/2dt
The integral of t1/2 is:
∫t1/2dt=23t3/2
Thus, we have:
s=√2Pm⋅23t3/2+C
Assuming the initial displacement is zero (i.e., C=0):
s=23√2Pmt3/2
1. Kinetic Energy:
KE=P⋅t
2. Velocity:
v=√2Pm⋅t1/2
3. Displacement:
s=23√2Pmt3/2
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Introductory
1 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.4
5 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A time varying power P=2t is applied on particle of mass m. find.
(a) kinetic energy and velocity of particle as function of time.
(b) average power over a time intrval from t=0 to t=t.
View SolutionA constant force (F) is applied on a stationary particle of mass m, the velocity attained by the particle in a certain interval of time will be proportional to
View SolutionA constant force(F) is applied on a stationary particle of mass 'm'. the velocity attained by the particle in a certain interval of time will be proportional to
View SolutionA constant force(F) is applied on a stationary particle of mass 'm'. The velocity attained by the particle in a certain displacement will be proportional to
View SolutionA constant power P is applied to a particle of mass m. The distance traveled by the particle when its velocity increases from v1 to v2 is (neglect friction):
View SolutionConstant power P is supplied to a particle having mass m and initially at rest. choose correct graph.
View Solutionvelocity time graph of a particle is shown in figure. Find displacement of the particle.
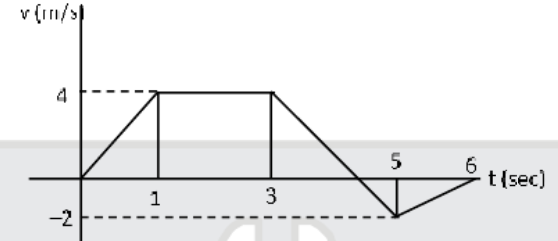
View SolutionA particle of mass 1 kg has a velocity of 2m/s. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View SolutionThe displacement of a particle as a function of time is shown in . It indicates
 .
.
View SolutionVelocity of a particle at time t=0 is 2ˆi m/s. A constant acceleration of 2ms2 acts on the particle for 2s at an angle of 60∘ with its initial velocity. Find the magnitude of velocity and displacement of particle at the end of t=2s.
View Solution
