Constant power P is supplied to a particle having mass m and initially at rest. choose correct graph.
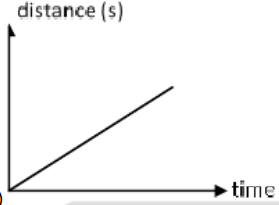


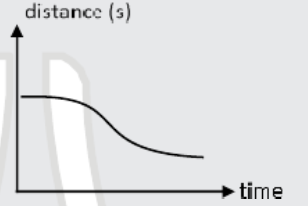
The correct Answer is:C
To solve the problem of determining the correct graph for a particle under constant power, we can follow these steps:
Step 1: Understand the relationship between power, work, and kinetic energy
Given that constant power P is supplied to a particle of mass m that starts from rest, we can relate power to kinetic energy. The work done by the power over time t is equal to the change in kinetic energy.
Step 2: Relate power to kinetic energy
The work done W by the power over time t can be expressed as:
W=P⋅t
This work is equal to the kinetic energy KE of the particle:
W=12mv2
Setting these two equations equal gives:
P⋅t=12mv2
Step 3: Solve for velocity v
Rearranging the equation for v:
v2=2Ptm
Taking the square root gives:
v=√2Pmt
Step 4: Find the relationship between distance s and time t
The distance s traveled by the particle can be found by integrating the velocity over time:
s=∫t0vdt
Substituting the expression for v:
s=∫t0√2Pmt′dt′
Step 5: Perform the integration
The integral can be computed as follows:
s=√2Pm∫t0(t′)1/2dt′
The integral of (t′)1/2 is:
∫(t′)1/2dt′=23(t′)3/2
Evaluating this from 0 to t gives:
s=√2Pm⋅23t3/2
Thus, we have:
s=23√2Pmt3/2
Step 6: Determine the relationship between s and t
From the final expression, we can see that:
s∝t3/2
This indicates that the graph of s versus t will be a curve that is concave upward, resembling a parabola.
Conclusion
The correct graph representing the relationship between distance s and time t is a concave upward parabola.
---
Given that constant power P is supplied to a particle of mass m that starts from rest, we can relate power to kinetic energy. The work done by the power over time t is equal to the change in kinetic energy.
The work done W by the power over time t can be expressed as:
W=P⋅t
This work is equal to the kinetic energy KE of the particle:
W=12mv2
Setting these two equations equal gives:
P⋅t=12mv2
Rearranging the equation for v:
v2=2Ptm
Taking the square root gives:
v=√2Pmt
The distance s traveled by the particle can be found by integrating the velocity over time:
s=∫t0vdt
Substituting the expression for v:
s=∫t0√2Pmt′dt′
The integral can be computed as follows:
s=√2Pm∫t0(t′)1/2dt′
The integral of (t′)1/2 is:
∫(t′)1/2dt′=23(t′)3/2
Evaluating this from 0 to t gives:
s=√2Pm⋅23t3/2
Thus, we have:
s=23√2Pmt3/2
From the final expression, we can see that:
s∝t3/2
This indicates that the graph of s versus t will be a curve that is concave upward, resembling a parabola.
The correct graph representing the relationship between distance s and time t is a concave upward parabola.
Topper's Solved these Questions
Similar Questions
A constant power P is applied on a particle of mass m. find kintic energy, velocity and displacement of particle as function of time t.
View SolutionA constant power P is applied to a particle of mass m. The distance traveled by the particle when its velocity increases from v1 to v2 is (neglect friction):
View Solution
Knowledge Check
The reduce mass of two particles having masses m and 2 m is
A2 mB3 mC2 m/3Dm/2
Two spherical shells have masses mand 2m as shows. Choose the correct options.
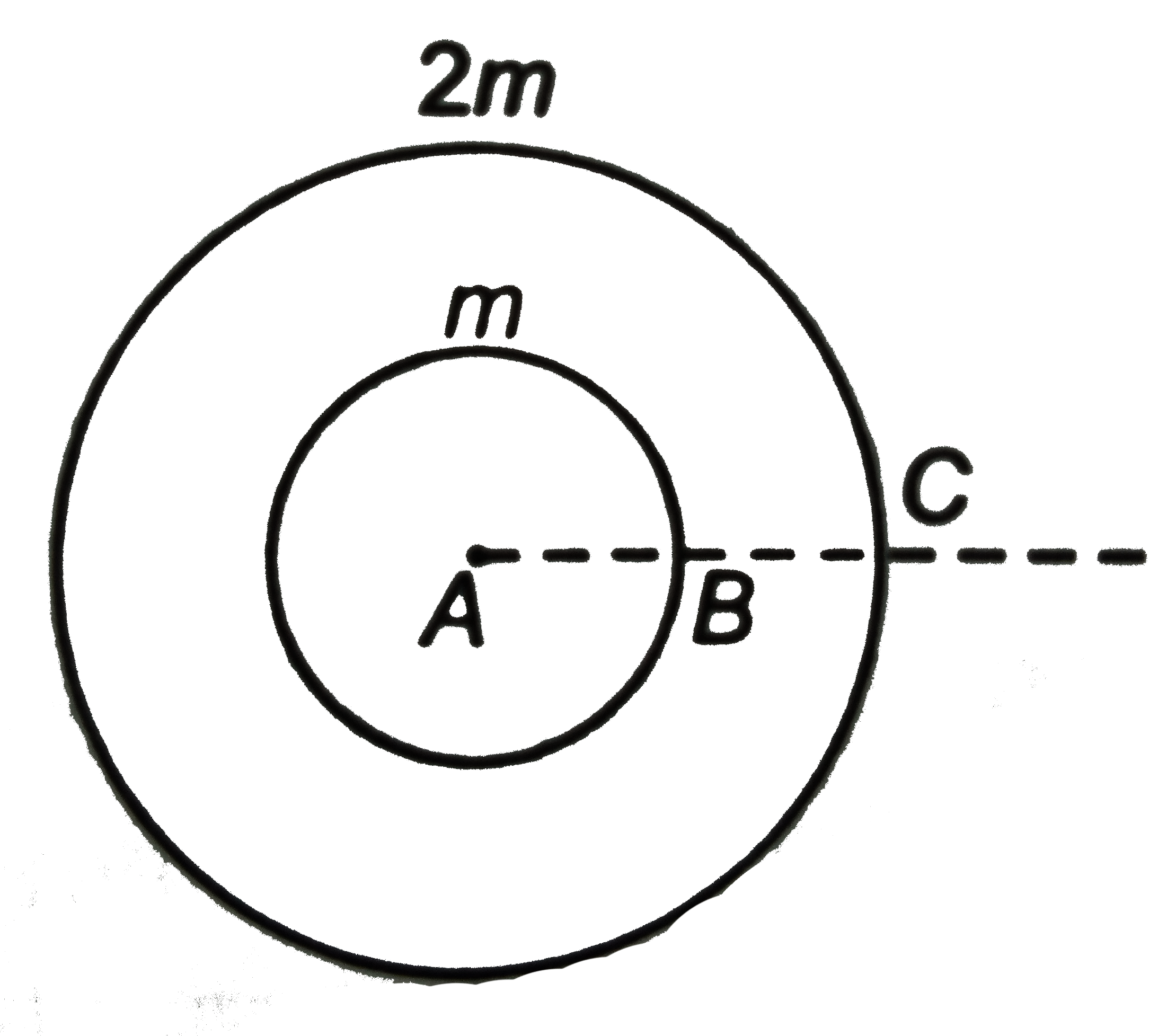
View SolutionA time varying power P=2t is applied on particle of mass m. find.
(a) kinetic energy and velocity of particle as function of time.
(b) average power over a time intrval from t=0 to t=t.
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionThe figure shows the force (F) versus displacement (s) graph for a particle of mass m=2kg initially at rest.
(i) The maximum speed of the particle occurs at x = …..m
(ii) The maximum speed of the particle is ….ms−1
(iii) The particle once again has its speed zero at x =....m
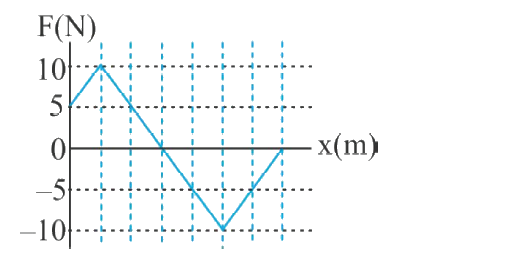
View SolutionAcceleration vs time graph is shown in the figure for a particle moving along a straight line. The particle is initially at rest. Find the time instant(s) when the particle comes to rest?
View SolutionThe power supplied by a force acting on a particle moving in a straight line is constant. The velocity of the particle varies with the displacement x as :
View SolutionA constant force F is applied on a spring block system as shown in figure. The mass of the block is m and spring constant is k. The block is placed over a smooth surface. Initially the spring was unstretched. Choose the correct alternative(s)

View Solution
