A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial value of x is
√(3H+4h)h
√(3h+4H)h
√(3H−4h)h
√(3H−3h)h
The correct Answer is:C
t=√2hg⇒∴X=vt=√(3H−4h)h.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Subjective
24 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.1
1 Video
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 More Than One Correct
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height H/2. The lower density liquid is open to the atmoshpere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) corss-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid interface with the length L/4 in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0.
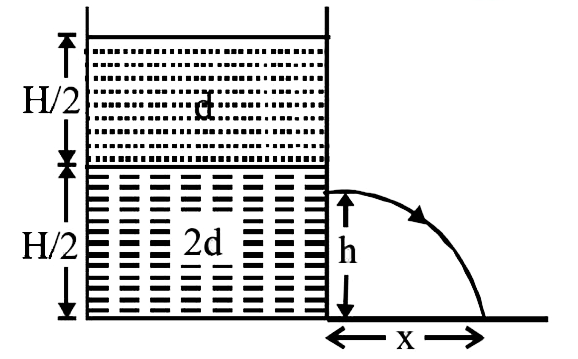
(a) A homogeneous solid cylinder of length L(L<H/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid. Determine:
(i) the density D of the solid and
(ii) the total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). Determine:
(i) the initial speed of efflux of the liquid at the hole,
(ii) the horizontal distance x travelled by the liquid initially, and
(iii) the height hm at which the hole should be punched so that the liquid travels the maximum distance xm initially. Also calculate xm.
View Solution
Knowledge Check
A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder isAv=√g3[3H+4h]Bv=√g3[4H−3h]Cv=√g3[3H−4h]DNone of theseA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The density D of the material of the floation cylinder isA5d/4B3d/4C4d/5D4d/3A container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container isAp0+(6L+H)4dgBp0+(L+6H)4dgCp0+(L+3H)4dgDp0+(L+2H)4dg
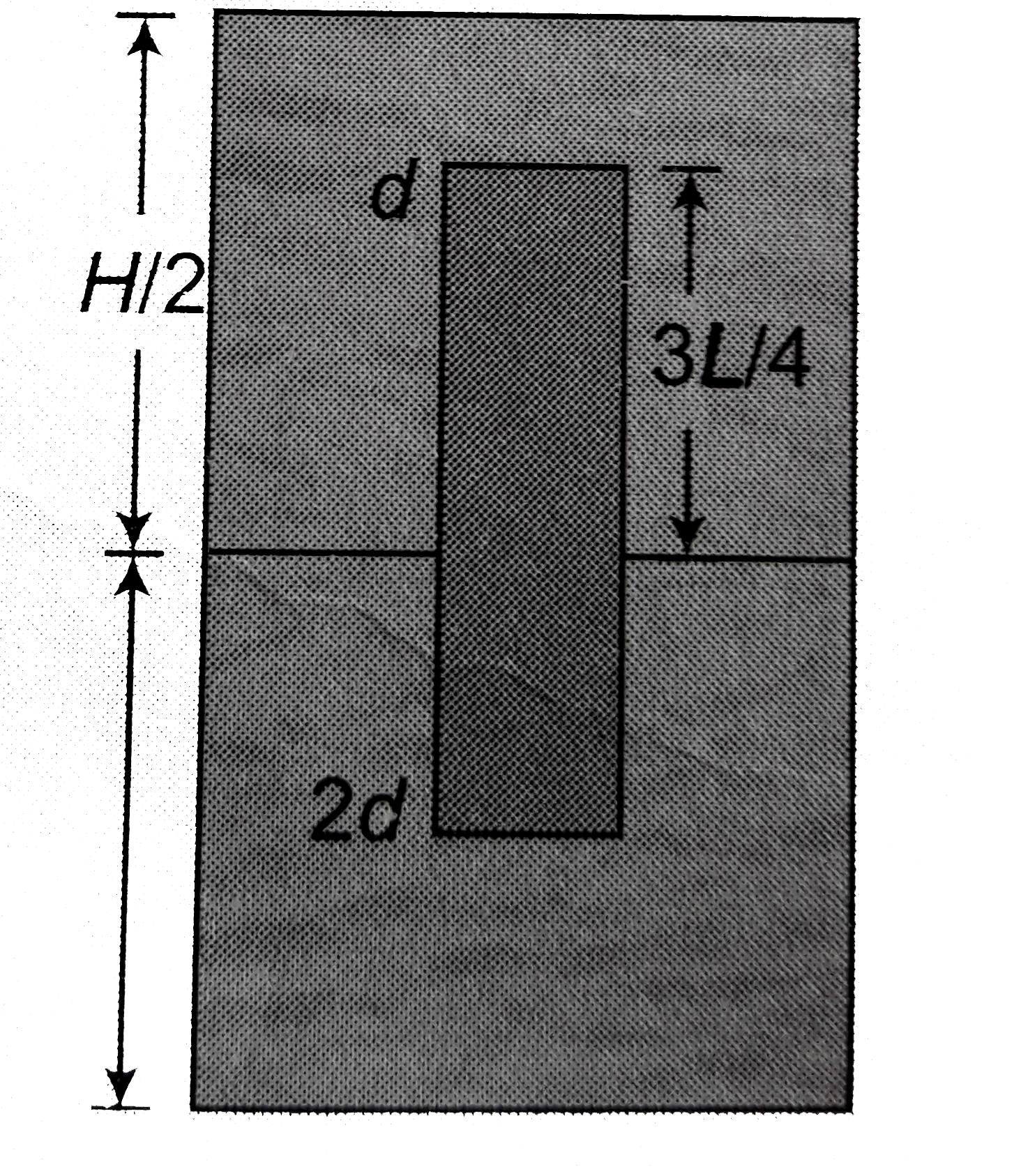
A container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d, each of height H/2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L<H2), cross-sectional area A/5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L/4 denser liquid. Determine
(a) density D of the solid and
(b) the total pressure at the bottom of the container. (Atmospheric pressure =P0).
 .
.
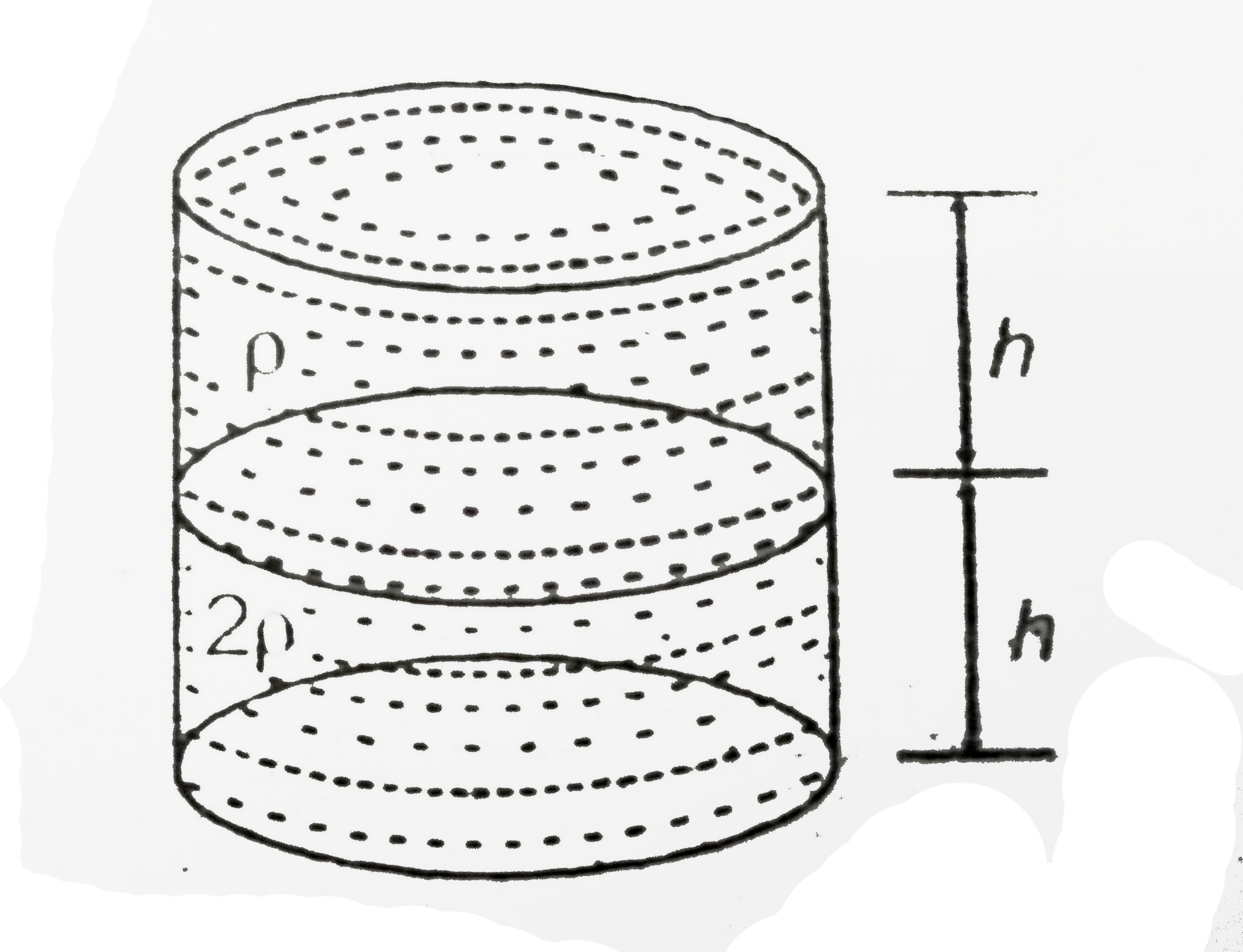
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H2 as shown in figure. The lower density liquid is open to the atmosphere having pressure P0.
(a) A homogeneous solid cylinder of length L(L<H2) cross-sectional area A5 is immersed such taht it floats with its axis vertical at the liquid-liquid interface with the length L4 in the denser liquid. Datermine:

(i) The density D of the solid and
(ii) The total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s<<A) is puched on the vertical side of the container at a height h(h−(H2)). Determine :
(i) The initial speed of the efflux of the liquid at the hole
(ii) The horizontal distance x travelled by the liquid initially and
(iii) The height hm at which the hole should be punched so that the liquid travels the maximum distance xm. initially. Also calculate xm. [ Neglect air resistance in these calculations ]

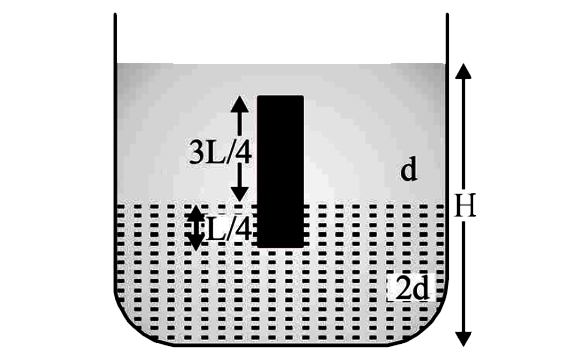
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
View SolutionA container of large uniform cross sectional area A resting on a horizontal surface holds two immiscible non-viscous and incompressible liquids of density d and 3d each of height H/2. The lower density liquid is open to the atmosphere having pressure Po. A tiny hole of area a (a<<A) is punched on the vertical side of the lower container at a height h(0<h<H2) for which range is maximum.
View Solution