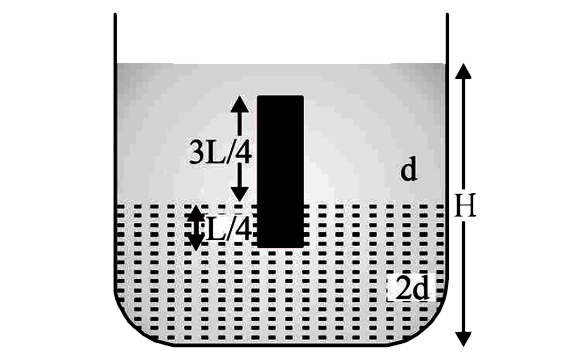
A container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height H2 as shown in figure. The lower density liquid is open to the atmosphere having pressure P0.
(a) A homogeneous solid cylinder of length L(L<H2) cross-sectional area A5 is immersed such taht it floats with its axis vertical at the liquid-liquid interface with the length L4 in the denser liquid. Datermine:
![A container of large uniform cross-sectional area A resting on a horizontal surface, holds two immiscible, non-viscous and incompressible liquids of densities d and 2d, each of height (H)/(2) as shown in figure. The lower density liquid is open to the atmosphere having pressure P(0). (a) A homogeneous solid cylinder of length L(L lt (H)/(2)) cross-sectional area (A)/(5) is immersed such taht it floats with its axis vertical at the liquid-liquid interface with the length (L)/(4) in the denser liquid. Datermine: (i) The density D of the solid and (ii) The total pressure at the bottom of the container. (b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s (s lt lt A) is puched on the vertical side of the container at a height h (h - ((H)/(2))). Determine : (i) The initial speed of the efflux of the liquid at the hole (ii) The horizontal distance x travelled by the liquid initially and (iii) The height h(m) at which the hole should be punched so that the liquid travels the maximum distance x(m). initially. Also calculate x(m). [ Neglect air resistance in these calculations ]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_WFPM_PHY_XI_C01_E01_123_Q01.png)
(i) The density D of the solid and
(ii) The total pressure at the bottom of the container.
(b) The cylinder is removed and the original arrangement is restored. A tiny hole of area s(s<<A) is puched on the vertical side of the container at a height h(h−(H2)). Determine :
(i) The initial speed of the efflux of the liquid at the hole
(ii) The horizontal distance x travelled by the liquid initially and
(iii) The height hm at which the hole should be punched so that the liquid travels the maximum distance xm. initially. Also calculate xm. [ Neglect air resistance in these calculations ]

The correct Answer is:(a) (i) Density =54d
(ii) Pressure =P0+14(6H+L)dg
(b) (i)v=√g2(3H−4h)
(ii) x=√h(3H−4h)
xmax=34H,hmax=3H8
(a) (i) Considering vertical equilibrium of cylinder :
Weight of cylinder = unthurst due to upper liquid
+ upthrust due to lower liquid
Note that h1 and h2≠H2
∴(A5)(L)D.g=(A5)(3L4)(d)g+(A5)(L4)(2d)(g)
∴D=(34)d+(14)(2d)
D=54d
(ii) Considering vertical equilibrium of two liquids and the cylinder.
(P−P0)A= weight of two liquids + weight of cylinder
∴P=P0+weight of liquids+weight of cylinderA...(1)
Now, weight of cylinder
=(A5)(L)(D)(g)=(A5Lg)(A5d)
=ALdg4
Weight of upper liquid =(H2Adg) and
Weight of lower liquid =H2A(2d)g=HAdg
∴ Total weight of two liquids =32HAdg
∴ From Eq. (1) pressure at the bottom of the container will be
P=P0+(32)HAdg+ALdg4A
or P=P0+dg(6H+L)4
(b) (i) Applying Bernoulli's theorem at 1 and 2
P0+dg(H2)+2dg(H2−h)=P0+12(2d)v2
Here, v is velocity of efflux at 2. Solving this, we get
v=√(3H−4h)g2
(ii) Time taken to reach the liquid to the bottom will be
t=√2h/g
/ Horizontal distance x travelled by the liquid is
x=vt=√(3H−4h'g2)(√2hg)

(iii) For x to be maximum
dxdh=0
or 12√h(3H−4h)(3H−8h)=0 or h=3H8
Therefore, x will be maximum at h=3H8.
The maximum value of x will be
xm=√3H83H−43H8
xm=34H
Topper's Solved these Questions
Similar Questions

A jar filled with two non-mixing liquid 1 and 2 having densities ρ1 and ρ2 respectively. A solid ball, made of a material of density ρ3 is dropped in the jar. It come to equilibrium in the position shown in the figure. Which of the following is true for ρ1,ρ2 and ρ3?
View SolutionOn moving a charge of 20 coulomb by 2cm, 2J of work is done , the potential difference between the points is .
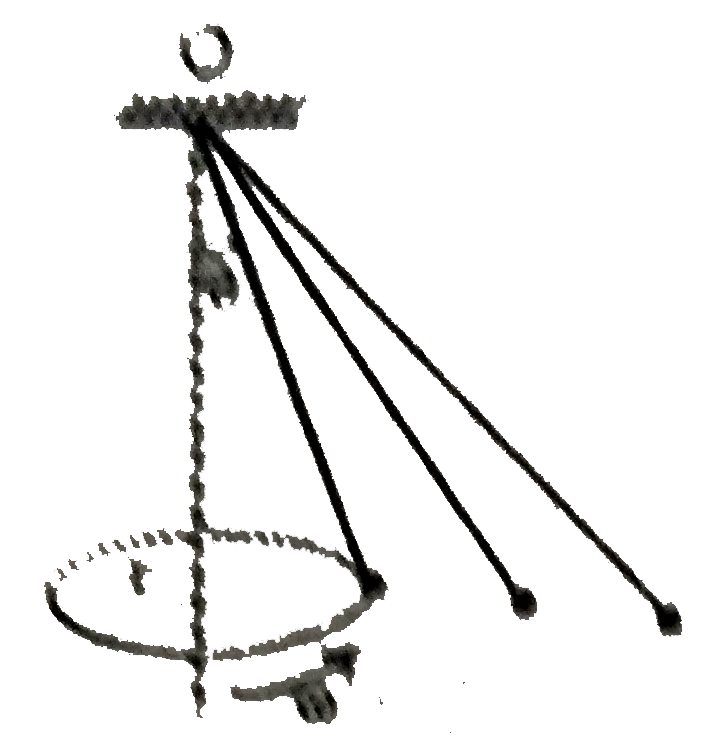
View SolutionThree masses of small size are attached by light inextensible strings of various lengths to a point O on the ceiling. All of the masses swing round in horizontal circles of various radii with the same angular frequency ω (one such circle is drawn in the shown figure.) Then pick up the correct statement.
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P_0 . Then density D of solid is given by
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The density D of the material of the floation cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The total pressure with cylinder, at the bottom of the container is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H/2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) and cross-sectional area A/5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid,

The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(s<<A) is punched on the vertical side of the container at a height h(h<H/2). As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface.
The initial speed of efflux without cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial value of x is
View SolutionA container of large uniform cross sectional area A resting on a horizontal surface holds two immiscible non-viscous and incompressible liquids of density d and 3d each of height H/2. The lower density liquid is open to the atmosphere having pressure P_o . A tiny hole of area a (a lt lt A) is punched on the vertical side of the lower container at a height h (0 lt h lt H/2) for which range is maximum.
View SolutionA container of a large uniform cross-sectional area A resting on a horizontal surface holds two immiscible, non viscous and incompressible liquids of densities d and 2d , each of height H//2 as shown in figure. The lower density liquid is open to atmosphere. A homogeneous solid cylinder of length L(L lt (H)/(2)) , cross-sectional area A//5 is immersed such that it floats with its axis vertical of the liquid-liquid interface with length L//4 denser liquid. Determine (a) density D of the solid and (b) the total pressure at the bottom of the container. (Atmospheric pressure = P_0 ). .
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holds two-immiscible, non-viscous & incompressible liquids of densities d & 2d, each of height H/2. The lower density liquid is open to the atmoshpere having pressure P0. A homogeneous solid cylinder of length L(L<H/2) corss-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid interface with the length L/4 in the denser liquid. Determine : (i) The density D of the solid & (ii) The total pressure at the bottom of the container.
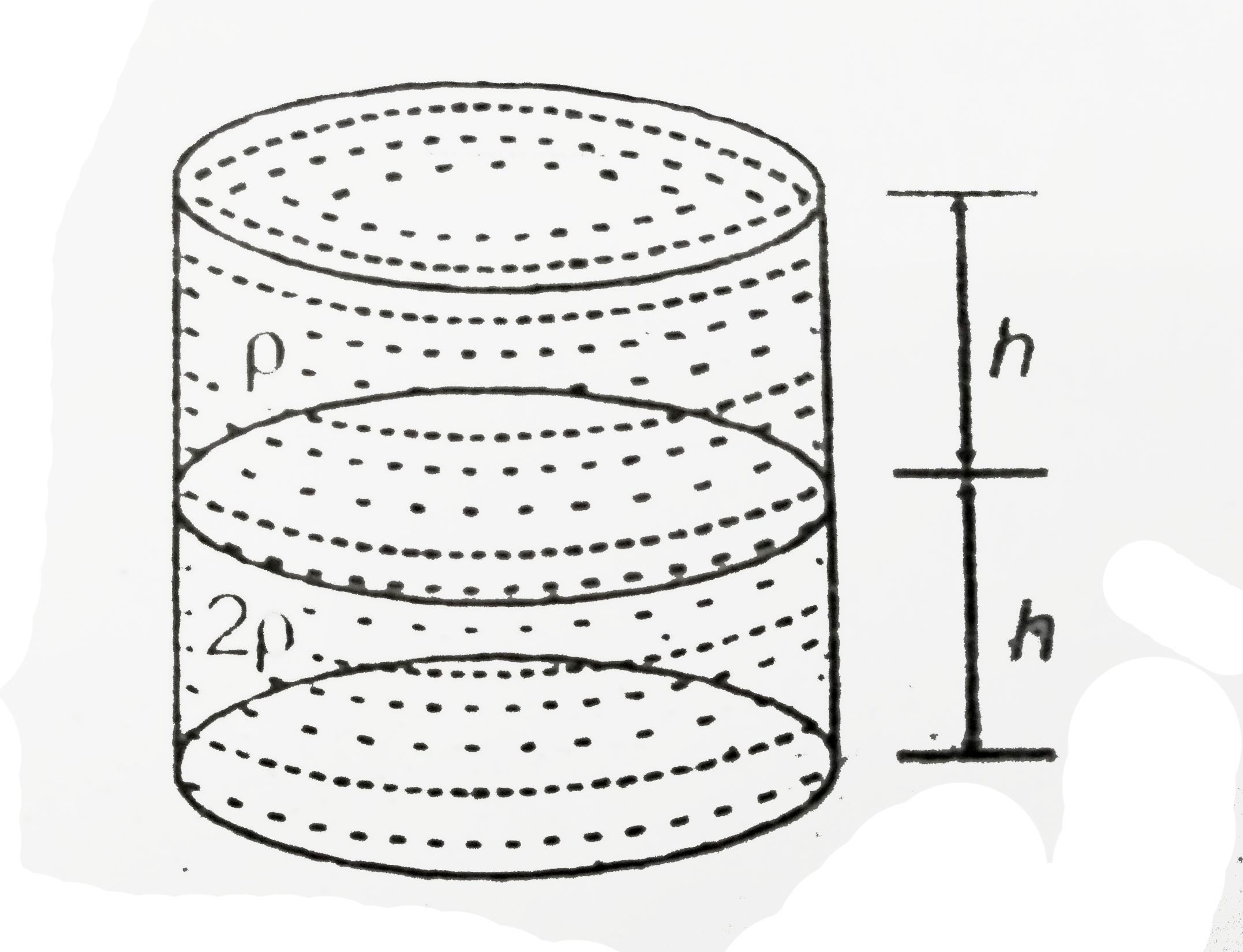
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
View SolutionA vessel of large uniform cross-sectional area resting on a horizontal surface holds two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H/2. If a small hole is punched on the vertical side of the container at a heighth h(h<H2) the efflux speed of the liquid al the hole is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscous and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The density D of the material of the floating cylinder is
View SolutionA container of large uniform cross-sectional area A resting on a horizontal surface, holes two immiscible, non-viscon and incompressible liquids of densities d and 2d each of height H//2 as shown in the figure. The lower density liquid is open to the atmosphere having pressure P_(0) . A homogeneous solid cylinder of length L(LltH//2) and cross-sectional area A//5 is immeresed such that it floats with its axis vertical at the liquid-liquid interface with length L//4 in the denser liquid, The cylinder is then removed and the original arrangement is restroed. a tiny hole of area s(sltltA) is punched on the vertical side of the container at a height h(hltH//2) . As a result of this, liquid starts flowing out of the hole with a range x on the horizontal surface. The initial speed of efflux without cylinder is
View SolutionA homogeneous solid cylinder of length L(LltH/2), cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the figure. The lower density liquid is open to atmosphere having pressure P0. Then density D of solid is given by
View Solution
