A converging lens of focal length $f_{1}$ is placed coaxially in contact with a diverging lens of focal length $f_{2} ((f_{1} > f_{2})$ . Determine the power and nature of the combination in terms of $f_{1}$ and $f_{2}$ .

Text Solution

Verified by Experts

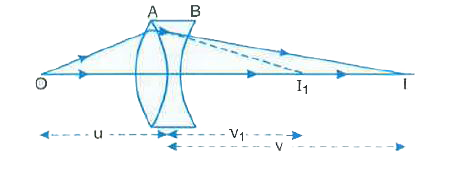
Consider two thin lenses A and B of focal lengths $f_{1}$ and $f_{2}$ placed in contact. Let a point object be placed at O, beyond the focus of first lens A. Lens A forms a real image at $I_{1}$ . This image serves as a virtual object for second lens B and the final real image is formed at I.
For image $I_{1}$ formed by first lens, we have
$\frac{1}{v_{1}} - \frac{1}{u} = \frac{1}{f_{1}}$
and for the image I formed by the second lens, we have
$\frac{1}{v} - \frac{1}{v_{1}} - \frac{1}{f_{2}}$ ...(ii)
Adding (i) and (ii), we have
$\frac{1}{v} - \frac{1}{u} = \frac{1}{f_{1}} + \frac{1}{f_{2}}$ ...(iii)

If the two lens system is considered as equivalent to a single lens of focal length f, then
$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$ ..(iv)
Comparing (iii) and (iv), we get
$\frac{1}{f} = \frac{1}{f_{1}} + \frac{1}{f_{2}}$ or $P = P_{1} + P_{2}$
As 1st lens is converging one but 2nd lens is diverging, hence $f_{1}$ is +ve but /2 is -ve and moreover $f_{1} > f_{2}$ .
$∴ P = P_{1} + P_{2} = \frac{1}{f_{1}} + \frac{1}{(- f_{2})} = \frac{f_{1} - f_{2}}{f_{1} f_{2}} = - v e$ , i.e. the combination behaves as a diverging lens.

Two thin lenses of focal lengths $f_{1}$ and $f_{2}$ are in contact. The focal length of this combination is
A $\frac{f_{1} f_{2}}{f_{1} - f_{2}}$
B $\frac{f_{1} f_{2}}{f_{1} + f_{2}}$
C $\frac{2 f_{1} f_{2}}{f_{1} - f_{2}}$
D $\frac{2 f_{1} f_{2}}{f_{1} + f_{2}}$
Two thin lenses of focal length $f_{1}$ and $f_{2}$ are in contact and coaxial. The power of the combination is
A $\sqrt{\frac{f_{1}}{f_{2}}}$
B $\sqrt{\frac{f_{2}}{f_{1}}}$
C $\frac{f_{1} + f_{2}}{f_{1} f_{2}}$
D $\frac{f_{1} + f_{2}}{f_{1} f_{2}}$
Two thin lenses of focal lengths $f_{1} and f_{2}$ are in contact and conxial. The power of the combination is
A $\frac{f_{1} + f_{2}}{f_{1} f_{2}}$
B $\sqrt{\frac{f_{1}}{f_{2}}}$
C $\sqrt{\frac{f_{2}}{f_{1}}}$
D $\frac{f_{1} + f_{2}}{2}$