A convex spherical refracting surfaces separates two media glass and air (μg=1.5). If the image is to be real, at what minimum distance u should the object be placed in air if R is the radius of curvature
u>3R
u>2R
t–4R
t–R
The correct Answer is:B

1.5v−1.0−u=1.5−1.0+R
or 1.5v=−1u+12R
For image to real (for negative value of u) v should
be positive. Hence, 1t–12Roru>2R.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A spherical surface of radius R ssparates two media of refractive indices μ1 and μ1 as shown in figure., Where should an object be placed in medium 1 so that a real image is formed in medium 2 at the same distance?
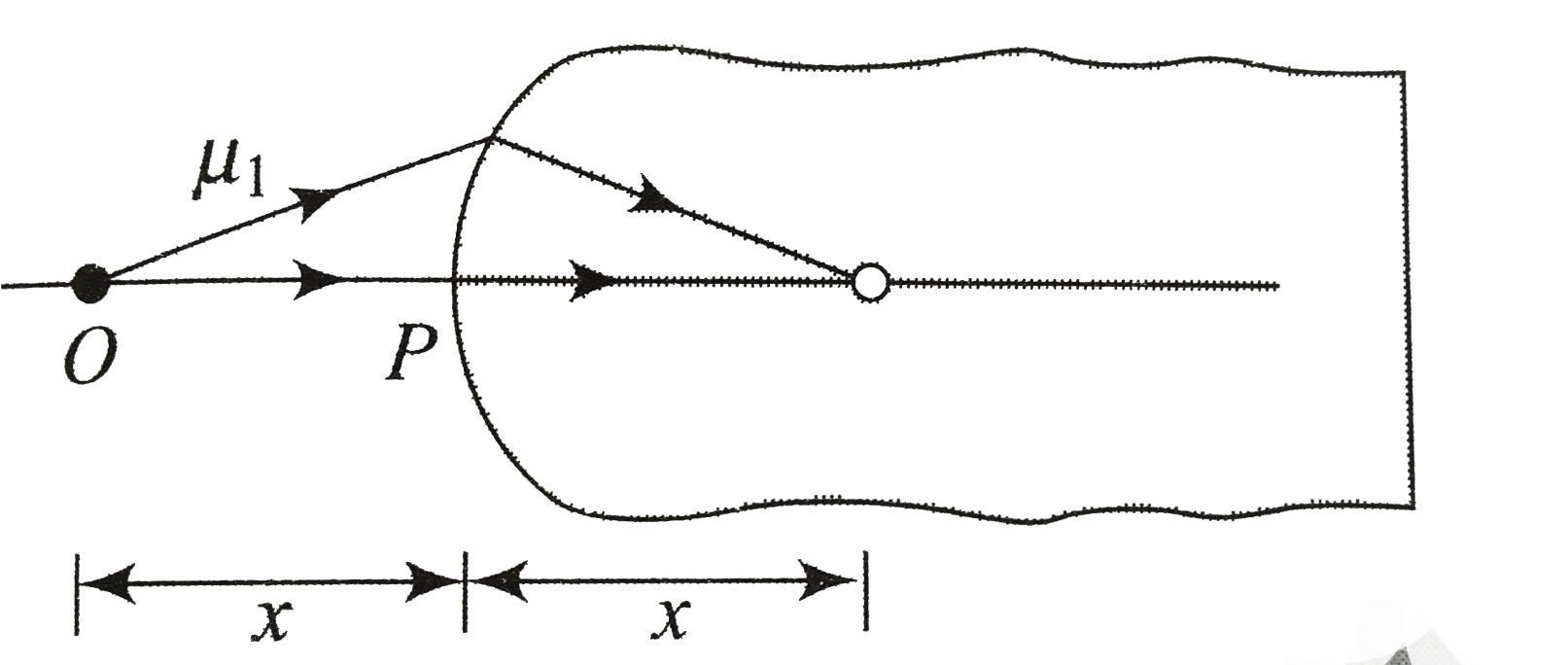
View SolutionThe image of an object placed in air formed by a convex refracting surface is at a distance of 10 m behind the surface. The image is real and is at 2rd3 of the distance of the object from the surface. The wavelength of light inside the surface is 23 times the wavelength in air. The radius of the curved surface is x13m. The value of 'x' is _________.
View Solution
Knowledge Check
Refraction takes place at a convex spherical boundary separating glass-air medium. For the image to be real, the object distance (μg=3/2) should be /is
Agreater than three times the radius of curvature of the refracting surfaceBgreater than two times the radius of curvature of the refracting surfaceCgreater than the radius of curvature of the refracting surfaceDindependent of the radius of curvature of the refracting surfaceRefraction takes place at a concave spherical boundary separating glass air medium. For the image to be real, the object distance (μg=3/2)
Ashould be greater than three times the radius of curvature of refracting surfaceBshould be greater than two times the radius of curvature of the refracting surfaceCshould be greater than the radius of curvature of refracting surfaceDis independent of the radius of curvature of the refracting surfaceWhat acn be the largest distance of an image of a real object from a convex mirror of radius of curvature 20 cm
A10 cmBInfinityC20 cmDNone
Show that for refraction at a concave spherical surface (separating glass-air medium), the distance of the object should be greater than three times the radius of curvature of the refracting surface for the image to be real.
View SolutionRefraction takes place at a convex spherical boundary separating air-glass medium. For the image to be real, the object distance (μg=3/2)
Note Object lying in the glass.
View SolutionThe minimum sum of the distances of a real object and a real image from a concave mirror of radius of curvature 20cm is:
View SolutionA convex mirror forms a real image 5 times the size of the object placed at a distance of 20cm from it. The radius of curvature of the mirror is
View SolutionRadius of curvature of a concave spherical surface separating air-glass medium is R. A point object is placed on the principal axis in the glass (mg=1.5). For the image to be real seen by

observer in air, distance of the object from P should be
View Solution
