A cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and MI is I. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
√2ghI+mr2
(2mghI+mr2)1/2
(2mghI+2mr2)1/2
√2gh
The correct Answer is:B
To solve the problem, we will use the principle of conservation of energy. Here's a step-by-step breakdown of the solution:
Step 1: Identify the initial and final states
Initially, the weight (mass m) is at a height h and is at rest. The potential energy at this point is given by:
PEinitial=mgh
The wheel is also at rest, so its initial kinetic energy is zero.
Step 2: Determine the final state after the weight has fallen
After the weight has fallen through a distance h, it has a velocity v and the wheel has an angular velocity ω. The potential energy of the weight has been converted into kinetic energy.
Step 3: Write the expression for final energy
The total energy at the final state consists of:
1. The kinetic energy of the falling mass:
KEmass=12mv2
2. The kinetic energy of the rotating wheel:
KEwheel=12Iω2
Thus, the total final energy is:
Efinal=12mv2+12Iω2
Step 4: Apply the conservation of energy principle
According to the conservation of energy:
PEinitial=Efinal
This gives us:
mgh=12mv2+12Iω2
Step 5: Relate linear and angular velocities
Since the cord does not slip on the wheel, the relationship between linear velocity v and angular velocity ω is given by:
v=rω
Substituting v in terms of ω into the energy equation:
mgh=12m(rω)2+12Iω2
This simplifies to:
mgh=12mr2ω2+12Iω2
Step 6: Factor out ω2
We can factor out ω2 from the right side:
mgh=12ω2(mr2+I)
Step 7: Solve for ω2
Rearranging the equation gives:
ω2=2mghmr2+I
Step 8: Take the square root to find ω
Taking the square root of both sides, we find:
ω=√2mghI+mr2
Conclusion
Thus, the angular velocity ω of the wheel after the weight has fallen through a distance h is:
ω=√2mghI+mr2
Initially, the weight (mass m) is at a height h and is at rest. The potential energy at this point is given by:
PEinitial=mgh
The wheel is also at rest, so its initial kinetic energy is zero.
After the weight has fallen through a distance h, it has a velocity v and the wheel has an angular velocity ω. The potential energy of the weight has been converted into kinetic energy.
The total energy at the final state consists of:
1. The kinetic energy of the falling mass:
KEmass=12mv2
2. The kinetic energy of the rotating wheel:
KEwheel=12Iω2
Thus, the total final energy is:
Efinal=12mv2+12Iω2
According to the conservation of energy:
PEinitial=Efinal
This gives us:
mgh=12mv2+12Iω2
Since the cord does not slip on the wheel, the relationship between linear velocity v and angular velocity ω is given by:
v=rω
Substituting v in terms of ω into the energy equation:
mgh=12m(rω)2+12Iω2
This simplifies to:
mgh=12mr2ω2+12Iω2
We can factor out ω2 from the right side:
mgh=12ω2(mr2+I)
Rearranging the equation gives:
ω2=2mghmr2+I
Taking the square root of both sides, we find:
ω=√2mghI+mr2
Thus, the angular velocity ω of the wheel after the weight has fallen through a distance h is:
ω=√2mghI+mr2
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (B) Chapter Exercises
25 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.3
15 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A cord is wound round the circumference of a solid cylinder radius R and mass M. The axis of the cylinder is horizontal. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h.

If the mass starts from rest and falls a distance h, then its speed at that instant is:
View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA metallic ring of radius r with a uniform metallic spoke of negligible mass and length r is rotated about its axis with angular velocity ω in a perpendicular uniform magnetic field B as shown in Fig. 3.163. The central end of the spoke is connected to the rim of the wheel through a resistor R as shown. The resistor does not rotate, its one end is always at the center of the ring and the other end is always in as shown is needed to maintain constant angular velocity of the wheel. F is equal to (the ring and the spoke has zero resistance)

View SolutionA dics is rotating in a room. A boy standing near the rim of the disc of radius R finds the water droplet falling from the ceiling is always falling on his head. As one drop hits his head, other one starts from the ceiling. If height of the roof above his head is H , then angular velocity of the disc is
View SolutionOne end of a string is tied to a rigid support attached to roof and the other end is wound around a uniform wheel of radius r and mass m. The string is kept vertical and the wheel is released from rest. As the wheel descends show that (i) the tension in the string is one-third the weight of the wheel, (ii) the magnitude of the acceleration of the centre of mass is 2g/3 and (iii) the speed of the centre of mass is (4gh/3)1/2

View SolutionA bit of mud stuck to a bicycle's front wheel of radius r detaches and is flung horizontally forward when it is at the top of the wheel. The bicycle is moving forward at a speed v and it is rolling without slipping. The horizontal distance travelled by the mud after detaching from the wheel is:
View SolutionA heavy disc with radius R is rolling down hanging on two non-stretched string wound around the disc very tightly. The free ends of the string are attached to a fixed horizontal support. The strings are always tensed during the motion. At some instant, the angular velocity of the disc is ω, and the angle between the strings is α. Find the velocity of centre of mass of the disc at this moment

View SolutionAs shown in the figure, two bobs of masses m & 2m are tied by a massless string which is wound on a fly wheel (disc) of radius r and mass m. When released from rest the bob of mass 2m starts falling vertically. When it has covered distance of h, the angular speed of the wheel will be:
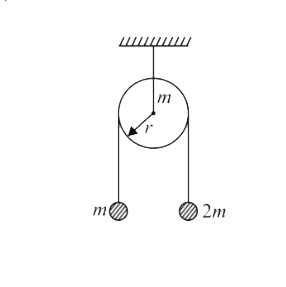
View SolutionAs shown in the figure, two bobs of masses m & 2m are tied by a massless string which is wound on a fly wheel (disc) of radius r and mass m. When released from rest the bob of mass 2m starts falling vertically. When it has covered distance of h, the angular speed of the wheel will be:

View SolutionA cord of negligible mass is wound round the rim of a flywheel of mass 20kg and radius 20cm. A steady pull of 25N is applied on the cord as shown in Fig. The flywheel is mounted on a horizontal axle with frictionless bearings.
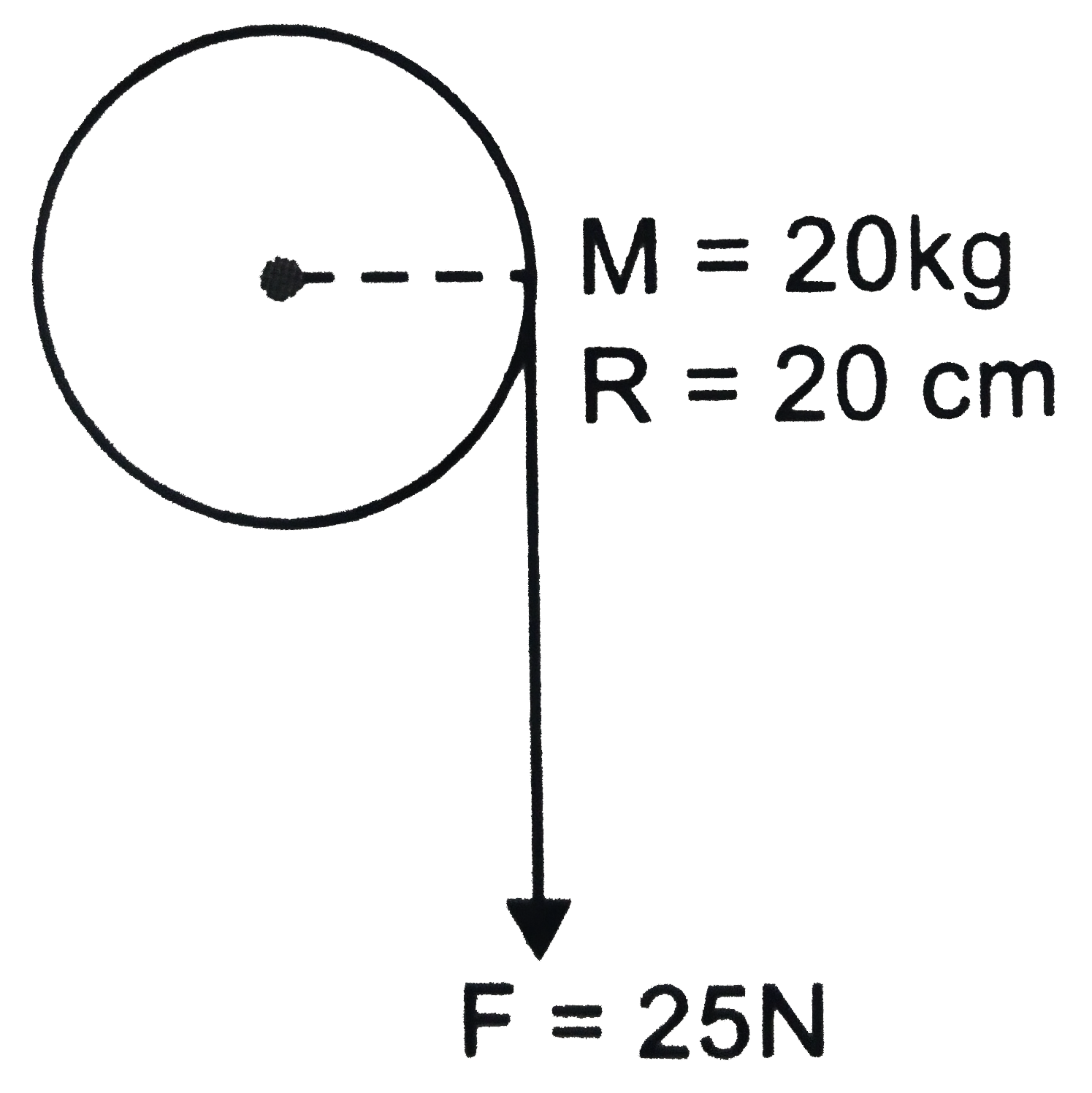
(a) Compute the angular acceleration of the wheel.
(b) Find the work done by the pull, when 2m of the cord is unwound.
(c) Find also the kinetic energy of the wheel at this point. Assume that the wheel stars from rest.
(d) Compare answers to parts (b)and (c).
View Solution
