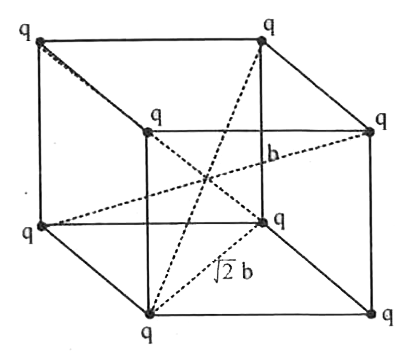
A cube of side 'b' has a charge 'q' at each of its vertices. Determine the potential and electric field due to this charge array at the centre of the cube.

Text Solution

Verified by Experts

$\frac{\sqrt{b^{2} + 2 b^{2}}}{2} = \frac{b}{2} \sqrt{3}$ is the centre
Distance of centre of the cube form one vertex is
$\frac{b}{2} \sqrt{3}$ . Hence potential due to charge $= \frac{1}{4 π ε_{0}} \frac{q}{\frac{b}{2} \sqrt{3}}$
Total potential $= \frac{8 \times q}{4 π ε_{0} \frac{b}{2} \sqrt{3}}$
$= \frac{2 \times 8 \times q}{4 π ε_{0} b \sqrt{3}} = \frac{4 q}{\sqrt{3} b π ε_{0}}$
Field =zero

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A cube of side x has a charge q at each of its vertices. Determine the potential due to this charge array at the center of the cube.
A $\frac{4 q}{3 π ε_{0} x}$
B $\frac{4 q}{\sqrt{3} π ε_{0} x}$
C $\frac{3 q}{4 π ε_{0} x}$
D $\frac{2 q}{\sqrt{3} π ε_{0} x}$
Question 2 - Select One
A hexagon of side 'a' has a charge 'q' at each of its vertices. The electric field at the centre of hexagon is
A $0$
B $\frac{1}{4 π \in_{0}} . \frac{q}{a^{2}}$
C $\frac{1}{4 π \in_{0}} . \frac{6 q}{a^{2}}$
D $\frac{1}{4 π \in_{0}} . \frac{6 q^{2}}{a^{2}}$
Question 3 - Select One
A cube of side 'a' has point charges +Q located at each of its vertices except at the origin where the charge is -Q. The electric field at the centre of cube is :

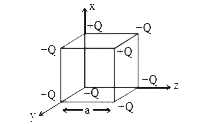A $\frac{- Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$
B $\frac{- 2 Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$
C $\frac{2 Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$
D $\frac{Q}{3 \sqrt{3} π ε_{0} a^{2}} (ˆ x + ˆ y + ˆ z)$

NEW JOYTHI PUBLICATION-ELECTROSTATIC POTENTIAL AND CAPACITANCE-Solution To Exercises From Ncert Texation

Home
Ask Doubt
Profile