Question

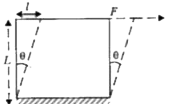
A cube of soft rubber of face area $0.02m^2$ whose lower face is fixed is sheared through an angle $2^{\circ }$ by a force of ${10}^{4}N$ acting tangential to the upper face. Calculate the rigidity modulus of the material.

Answer

`1.433 xx 10^(7) N //m^(2)`

Explanation

To solve the problem, we need to calculate the rigidity modulus (shear modulus) of the soft rubber cube using the given data. Here’s a step-by-step breakdown of the solution:

Step 1: Identify the Given Values
- Face area of the cube, \( A = 0.02 \, m^2 \)
- Force applied, \( F = 10^4 \, N \)
- Angle of shear, \( \alpha = 2^\circ \)

Step 2: Calculate the Shear Stress
Shear stress (\( \tau \)) is defined as the force applied per unit area. The formula for shear stress is:

\( \tau = \frac{F}{A} \)

Substituting the known values:

\( \tau = \frac{10^4 \, N}{0.02 \, m^2} = 5 \times 10^5 \, N/m^2 \)

Step 3: Calculate the Shear Strain
Shear strain (\( \gamma \)) can be approximated by the tangent of the angle of shear. The formula is:

\( \gamma = \tan(\alpha) \)

Since \( \alpha = 2^\circ \), we convert it to radians for calculation if necessary, but for small angles, we can use:

\( \gamma \approx \tan(2^\circ) \approx 0.0349 \, \text{(using a calculator)} \)

Step 4: Use the Relationship Between Shear Stress, Shear Strain, and Rigidity Modulus
The relationship between shear stress, shear strain, and rigidity modulus (\( S \)) is given by:

\( \tau = S \cdot \gamma \)

Rearranging this gives:

\( S = \frac{\tau}{\gamma} \)

Step 5: Substitute the Values to Find Rigidity Modulus
Now, substituting the values of shear stress and shear strain into the equation:

\( S = \frac{5 \times 10^5 \, N/m^2}{0.0349} \)

Calculating this gives:

\( S \approx 1.43 \times 10^7 \, N/m^2 \)

Final Answer
The rigidity modulus of the material is approximately:

\( S \approx 1.43 \times 10^7 \, N/m^2 \)

---