A 4 cm cube has its upper face displaced by 0.1 mm by a tangential force of 8 kN. Calculate the shear modulus of the cube.
To calculate the shear modulus of the cube, we can follow these steps:
Step 1: Identify the dimensions of the cube and convert units
The side length of the cube is given as 4 cm. We need to convert this to meters for standard SI units, but since we will be working with dyne and cm², we can keep it in cm.
Step 2: Calculate the area of the face
The area A of the face of the cube over which the force is applied can be calculated using the formula:
A=l2
where l is the length of one side of the cube. Thus,
A=(4cm)2=16cm2
Step 3: Convert the displacement to cm
The displacement of the upper face is given as 0.1 mm. We need to convert this to centimeters:
Δl=0.1mm=0.1×110cm=0.01cm
Step 4: Convert the applied force to dynes
The applied force is given as 8 kN. We need to convert this to dynes:
F=8kN=8×103N=8×103×105dynes=8×108dynes
Step 5: Use the formula for shear modulus
The shear modulus η can be calculated using the formula:
η=F⋅LA⋅Δl
where L is the original length of the cube (4 cm), A is the area calculated earlier, and Δl is the displacement.
Substituting the values:
η=(8×108dynes)⋅(4cm)(16cm2)⋅(0.01cm)
Step 6: Calculate the shear modulus
Calculating the above expression:
η=(8×108)⋅416⋅0.01
=32×1080.16
=2×1010dyne/cm2
Final Answer
The shear modulus of the cube is 2×1010dyne/cm2.
---
The side length of the cube is given as 4 cm. We need to convert this to meters for standard SI units, but since we will be working with dyne and cm², we can keep it in cm.
The area A of the face of the cube over which the force is applied can be calculated using the formula:
A=l2
where l is the length of one side of the cube. Thus,
A=(4cm)2=16cm2
The displacement of the upper face is given as 0.1 mm. We need to convert this to centimeters:
Δl=0.1mm=0.1×110cm=0.01cm
The applied force is given as 8 kN. We need to convert this to dynes:
F=8kN=8×103N=8×103×105dynes=8×108dynes
The shear modulus η can be calculated using the formula:
η=F⋅LA⋅Δl
where L is the original length of the cube (4 cm), A is the area calculated earlier, and Δl is the displacement.
η=(8×108dynes)⋅(4cm)(16cm2)⋅(0.01cm)
Calculating the above expression:
η=(8×108)⋅416⋅0.01
=32×1080.16
=2×1010dyne/cm2
The shear modulus of the cube is 2×1010dyne/cm2.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Solved Examples6videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - MiscellaneousExamples4videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions469videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
A cube of side 40 cm has its upper face displaced by 0.1 mm by a tangential force of 8 Kn. The shearing modulus of cube is :-
View SolutionA 0.05m cube has its upper face displaced by 0.2cm by a tangential force of 8N. Calculate the shearing strain, shearing stress and modulus of rigidity of the material of the cube.
View SolutionA metallic cube whose each side is 10 cm is subjected to a shearing force of 100 kgf. Calculate the shearing produced.
View SolutionThe square on the diagonal of a cube has an area of 1875 sq. cm. Calculate:
the side of the cubeView SolutionOne of the square faces of a metal slab of side 50 cm and thickness 20 cm is rigidly fixed on a horizontal surface. If a tangential force of 30 N is applied to the top face and it is known that the shear modulus of the material is 4×1010N/m2, then the displacement (in m) of the top face is
View SolutionThe square on the diagonal of a cube has an area of 1875 sq. cm. Calculate:
the total surface area of the cube.View SolutionThe square on the diagonal of a cube has an area of 192cm2Calculate :
the side of the cube.View SolutionA cube of sponge rubber with edge length 5cm has a force of 2N applied horizontally to the top face (parallel to an edge) while the bottom face is held fixed. If the top face is displaced horizontally through a distance of 1mm, find the shear modulus for the sponge rubber. (in Nm2)
View SolutionFig. 4.11 shows a cube of each side 15 cm immersed in a tube containing water of density 103kgm−3 such that its top surface is 20 cm below the free surface of water.
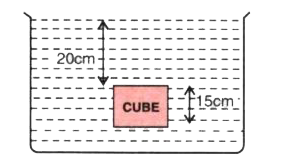
Calculate (i) the pressure at the top of cube,
(ii) the pressure at the bottom of cube,
(iii) the resultant pressure on cube.
(iv) the resultant thrust on cube.
Take atmospheric pressure = 105 Pa and g=9.8Nkg−1.View SolutionA shearing force of 106 N is applied on the top surface of a fixed cube of side 10 cm. If the top surface is displaced by 0.33 mm, find rigidity modulus of the material of the cube.
View Solution

