A cubical block of co-efficient of linear expansion αs is submerged partially inside a liquid of co-efficient of volume expansion γl. On increasing the temperature of the system by ΔT, the height of the cube inside the liquid remains unchanged. Find the relation between αsandγl.
The correct Answer is:A, B
Initially, at temperature T
FB=mg
Axρlg=Alρbg
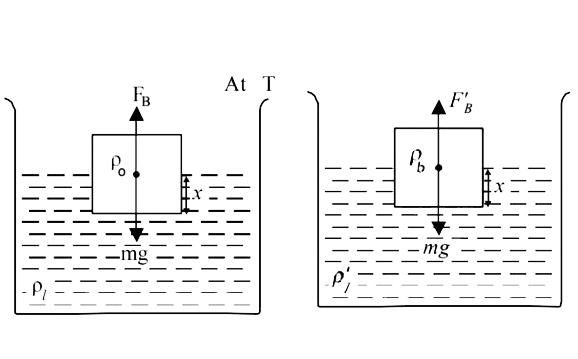
⇒xρl=Lρb…..(i)
At temperature T+ΔT
FB'=mg
A'xρ'lg=Alρbg[mgrema∈sthesameasabove]
Now, A'=A(1+2αΔT)
ρ'l=ρl(1−γΔT)
∴A(1+2αΔT)xρl(1−γΔT)=Lρbg
⇒xρl(1+2αΔT)(1−γΔT)=Lρb
⇒xρl(1+2αΔT)(1−γΔT)=xρl[From(i)]
⇒1+2αΔT−γΔT=1
⇒γ=2α
Topper's Solved these Questions
Similar Questions
A cube of coefficient of linear expansion alpah is floating in a bath containing a liquid of coefficeient of volume expansion γl. When the temperature is raised by ΔT, the depth upto which the cube is submerged in the liquid remains the same. Find relation between α and γl
View SolutionA solid cube is first floating in a liquid. The coefficient of linear expansion of cube is α and the coefficient of volume expansion of liquid is γ. On increasing the temperature of (liquid + cube) system, the cube will sink if

View Solution
Knowledge Check
A rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
AlαΔTBl(1+αΔT)Cl(1+2αΔT)Dnone of theseA rod of length l and coefficient of linear expansion α. Find increase in length when temperature changes from T to T+ ΔT
AlαΔTBl(1+αΔT)Cl(1+2αΔT)Dnone of theseA liquid with coefficient of volume expansion γ is filled in a container of a material having coefficient of linear expansion α . If the liquid overflows on heating, then
Aγ=3αBγ>3αCγ<3αDγ=α3
A liquid having coefficient of volume expansion γ0 is filled in a cylindrical glass vessel. Glass has a coefficient of linear expansion of αg. The liquid along with the container is heated to raise their temperature by ΔT. Mass of the container is negligible. (a) find relationship between αg and γ0 if it was found that the centre of mass of the system did not move due to heating.
(b) Find relationship between αg and γ0 if the fraction of volume of the container occupeid by the liquid does not change due to heating.
View SolutionA rod has variable co-efficient of linear expansion α=x5000. If length of the rod is 1 m . Determine increase in length of the rod in (cm) on increasing temperature of the rod by 100∘C.
_S01_121_Q01.png)
View SolutionConsider a cylindrical container of cross-section area A length h and having coefficient of linear expansion αc. The container is filled by liquid of real expansion coefficient γL up to height h1. When temperature of the system is increased by Δθ then
(a). Find out the height, area and volume of cylindrical container and new volume of liquid.
(b). Find the height of liquid level when expansion of container is neglected.
(c). Find the relation between γL and αc for which volume of container above the liquid level
(i) increases
(ii). decreases
(iii). remains constant.
(d). On the surface of a cylindrical container a scale is attached for the measurement of level of liquid of liquid filled inside it. If we increase the temperature of the temperature of the system by Δθ, then
(i). Find height of liquid level as shown by the scale on the vessel. Neglect expansion of liquid.
(ii). Find the height of liquid level as shown by the scale on the vessel. Neglect expansion of container.

View SolutionThe coefficient of linear expansion varies linearly from α1 and α2 in a rod of length l. Find the increase in length when its temperature is increased by ΔT.
View SolutionThe coefficient of linear expansion varies linearly from α1 and α2 in a rod of length l. Find the increase in length when its temperature is increased by ΔT.
View Solution
