A cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)
1.25 cm
2.5cm
5cm
7.5cm
The correct Answer is:C
Let h = height to of water column
then ρwgh+ρHgg(10−h)=ρCug10
⇒h+13.6(10−h)=73
⇒63=12.6h⇒h=5cm.
Topper's Solved these Questions
Similar Questions
(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?View SolutionA cubical block of iron 5 cm on each side is floating on mercury in a vessel. (i) what is the height of the block above mercury level ?
(ii) Water is poured in the vessel unitl it just covers the iron block. What is the height of water column . density of mercur 13.6gm/cm3. Density of iron 7.2 gm/cm3View Solution
Knowledge Check
- Question 1 - Select One
A piece of ice at 0∘C is added to a vessel containing water at 0∘C, then
Aall of the ice will meltBsome ice will meltCno ice will meltDthe temperature will decrease further - Question 2 - Select One
A cubical block of steel of each side equal to 1 is floating on mercury in vessel. The densities of steel and mercury are ρs and ρm. The height of the block above the mercury level is given by
Al(1+ρsρm)Bl(1−ρsρm)Cl(1+ρmρs)Dl(1−ρmρs)
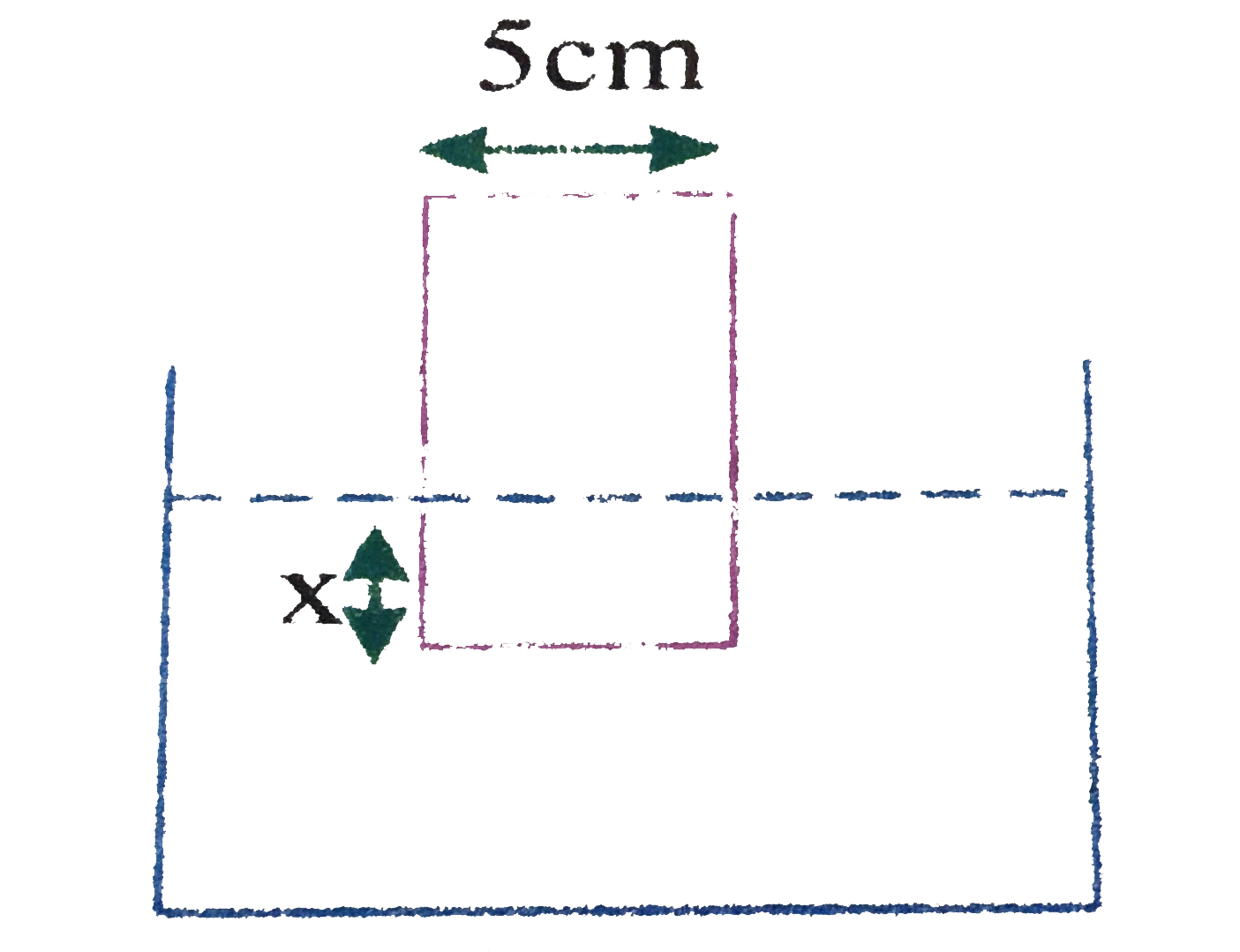
A cubical block of iron of side 5 cm is floating in mercury taken in a vessel. What is the height of the block above mercuery level.
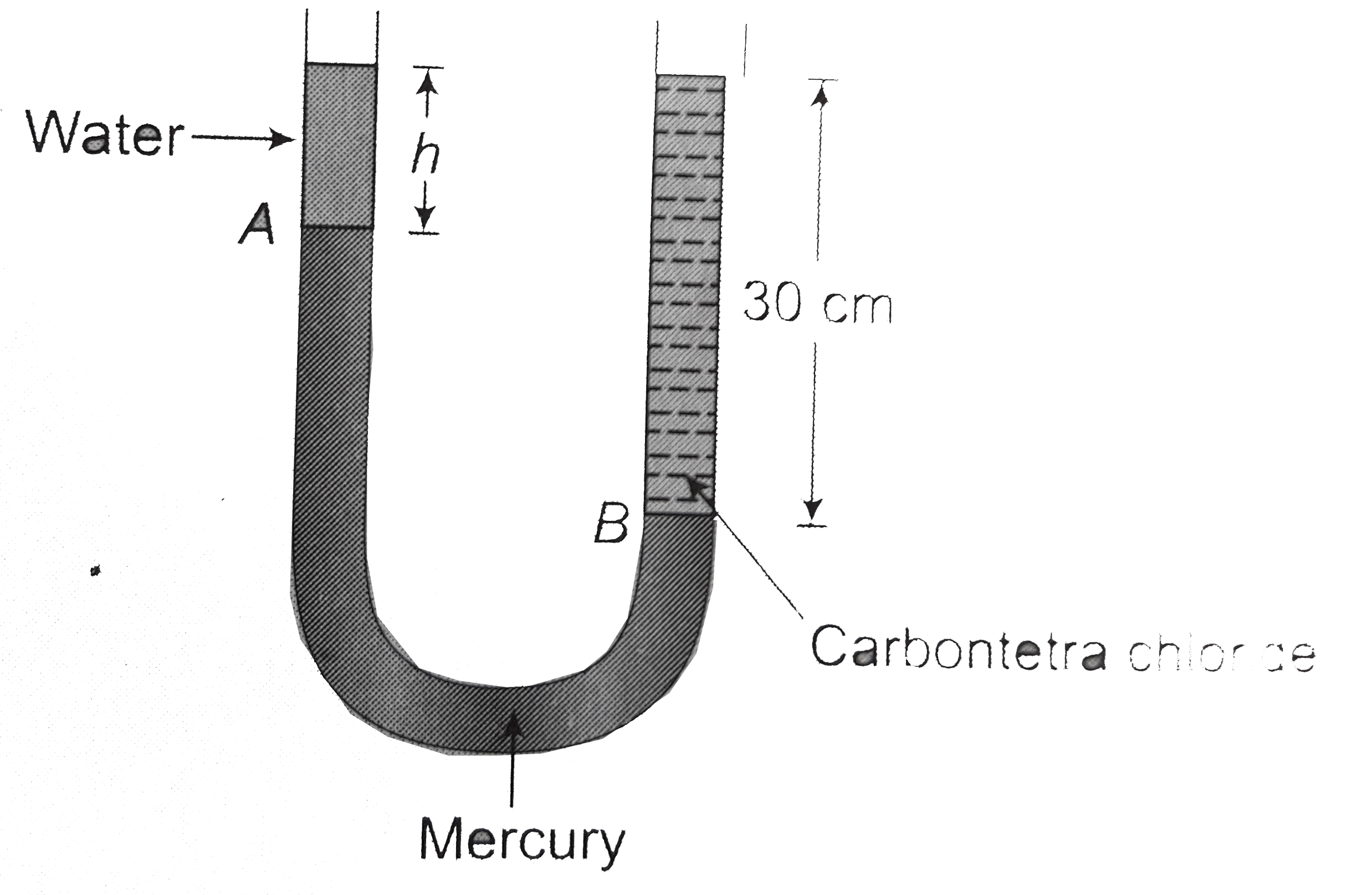
(ρHg=13.6g/cm3,ρFe=7.2g/cm3)View SolutionConsider the situation shown in diagram. Determine h
ρω=1g/cc.ρm=13.6g/cc
ρc=1.6g/cc.
 .View Solution
.View SolutionOne third height of a cubical block of edge 6cm is floating in kerosene oil of specific gravity 0.8. To make the block to be just immersed some water is poured. What is the height of the water column?
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View SolutionA cube of iron of edge 5cm floats on the surface of mercury, contained in a tank. Water is then poured on top, so that the cube just gets immersed. Find the depth of water layer. (Specific gravities of iron-and mercury are 7.8 and 13.6, respectively.)
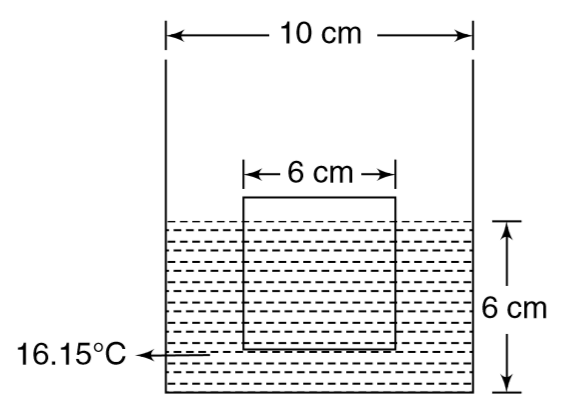
View SolutionA container has a square cross-section of 10cm×10cm. A cubical ice block of side length 6 cm is floating in water in the container. Water level in the container is 6 cm high. The ice block is at a temperature of 0∘C and the water is at 16.15∘C. Assume that heat exchange take place between the ice block and water only. What length of ice block will remain submerged in water when the system reaches thermal equilibrium? Assume that the ice block maintains its cubical shape as it melts. Take - density of ice =0.9g/cc, density of water = 1.0g/cc
Specific heat capacity of water =1calg−1.∘C−1, Specific latent heat of fusion of ice =80calg−1
 View Solution
View Solution

