A cube of iron of edge 5cm floats on the surface of mercury, contained in a tank. Water is then poured on top, so that the cube just gets immersed. Find the depth of water layer. (Specific gravities of iron-and mercury are 7.8 and 13.6, respectively.)
The correct Answer is:2cm
Let the depth of water layer be h1cm So, the depth to which the cube is immersed in mercury will be as follows:
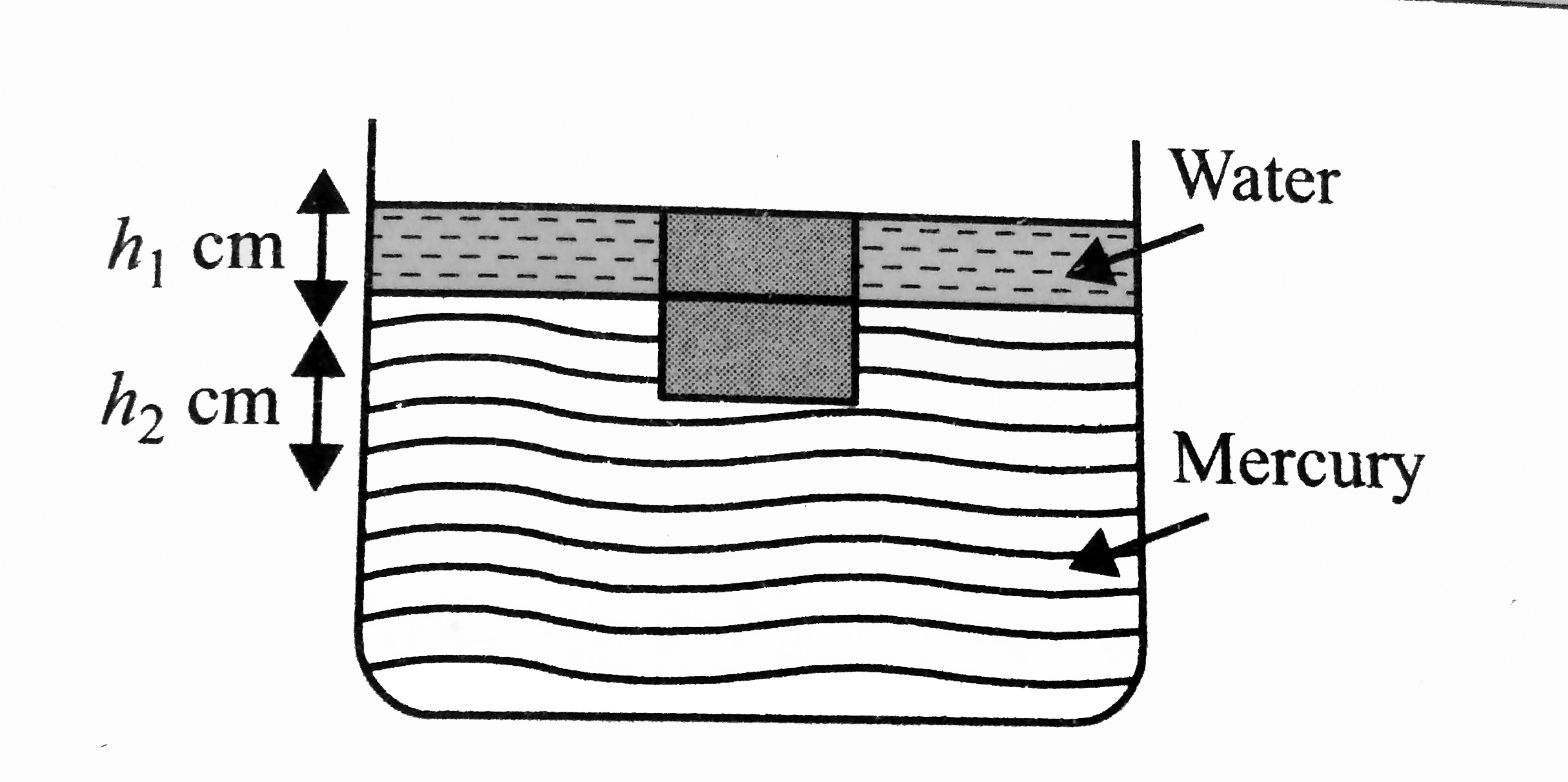
Weight of water displaced =(52h1g) dyn and weight of mercury displaced =52(5−h1)13.6gdyn.
Therefore, upthrust offered by water and mercury together is given by 52h1g+52(5−h1)13.6g
=52(68−12.6h1)gdyn
Weight of cube =53×8.56gdyn
From the principle of floatation we have
Upthrust = weight of the floating body
∴52(68−12.6h1)g=53×8.56g
⇒68−12.6h1=41.8
⇒h1=25.212.6=2cm
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Single Correct
95 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Multipe Correct
15 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.4
10 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
(i) A cubical metal block of side 10cm is floating in a vessel contatining mercury. The vesel has a square cross section of side length 15cm. Water is poured into the vessel so that the metal block just gets submerged. Calculate the mass of water that was poured into the vessel. It is given that relative density of the metal and mercury are 7.3 and 13.6 respectively.
(ii) In the last question, in place of water if we poured another liquid of relative density 'r' it was found that when the metal block ws just completely submerged it was no longer touching mercury. what is value of r?
View SolutionA cubical metal block of edge 12 cm floats in mercry with one fifth of the height inside the mercury. Water poured till the surface of the block is just immersed in it. Find the height of the block is just immersed in it. Find the height of the water column to be poured. Specific gravity of mercury =13.6.
View Solution
Knowledge Check
What mass of lead will weigh as much as 8 gm of iron when both are immersed in water ? (given specific gravities of iron and lead are 8 and 11 respectively).
A1.1 gmB2.2 gmC5.5 gmD7.7 gmA wooden cube is found to float in water with ½cm of its vertical side above the water. On keeping a weight of 50 gm over its top, it is just submerged in the water. The specific gravity of wood is
A0.8B0.9C0.85D0.95A cubical block of copper of side 10cm is floating in a vessel containing mercury. Water is poured into the vessel so that the copper block just gets submerged. The height of water column is
(ρHg=13.6g/cc,ρCu=7.3g/cc,ρwater=1gm/cc)A1.25 cmB2.5cmC5cmD7.5cm
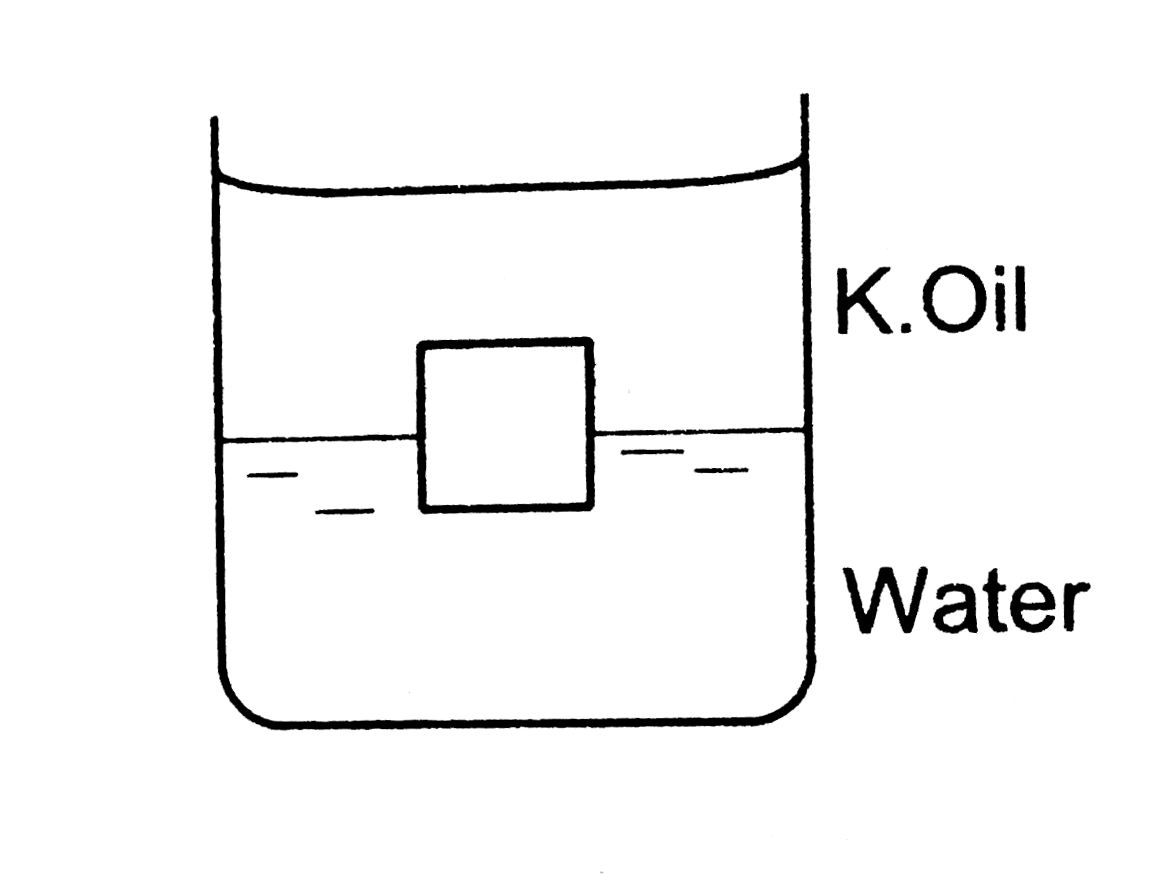
A cube of ice floats partly in water and partly in K.oil figure. Find the ratio of the volume of ice immersed in water to that in K.oil. Specific gravity of K.oil is 0.8 nd that of ice is 0.9.
View SolutionA cube of edge 15 cm is immersed completely in a rectangular vessel containing water. If the dimensions of the base of vessel are 20cm×15cm , find the rise in water level.
View SolutionA cylinder of iron floats vertically and fully immersed in a vessel containing mercury and water. Find the ratio of the length of the cylinder immersed in water to that immersed in mercury. (Relative density of mercury = 13.6 and that of iron = 7.78)
View SolutionA tank contains water on top of mercury . A cube of iron, 60mm along each edge, is sitting upright in equilibrium in the liquids. Find how much of it is in each liquid. The densities of iron and mercury are 7.7×103kg/m3 and 13.6×103kg/m3 respectively

View SolutionAn ice cube of side 1cm is floating at the interface of kerosene and water in a beaker of base area 10cm2. The level of kerosene is just covering the top surface of the ice cube.
a. Find the depth of submergence in the kerosene and that in the water.
b. Find the change in the total level of the liquid when the whole ice melts into water.

View Solution