A cubical block of ice of maas m and edge L is placed in a large tray of maas M. If the ie melts, how far does the centre of maas of the system ''ice plus tray'' come down?
If both assertion and reason are correct and reason is the correct explanation of the assertion.
If both assertion and reason are correct but reason is not the correct explanation of assertion
If assertion is correct but reason is incorrect.
If both assertion and reason are incorrect.
Centre of mass remains at the same place due to absence of external forces in gravity free space. Normal reaction between ice and tray remains zero
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
Explore 3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (MATRIX MATCH TYPE QUESTIONS) )
Explore 1 Video
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:MODERN PUBLICATIONChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS MULTIPLE CHOICE QUESTIONS (with more than one correct answer) )
Explore 35 Videos
- PHYSICAL WORLD Book:MODERN PUBLICATIONChapter:PHYSICAL WORLD Exercise:Revision exercises (Long answer questions)
Explore 6 Videos
- THERMAL PROPERTIES OF MATTERBook:MODERN PUBLICATIONChapter:THERMAL PROPERTIES OF MATTERExercise:CHAPTER PRACTICE TEST
Explore 15 Videos
Similar Questions
Consider a gravity free hall in which a tray of mas M, carrying a cubical block of icce of mas m and edge L, is at rest in the middle.. If the ice melts, by what distnce does the centre of mass of the tray plus the ice system descend?
View SolutionA cubical ice block of side length 'a' is floating in water in a beaker. Find the change in height of the centre of mass of (water+ice) system when the ice block melts completely. It is given that ratio of mass of water to mass of ice originally in the containe is 4:1.
View Solution
Knowledge Check
A wooden cubical block ABCDEFG of mass m and side a is wrapped by a square wire loop of perimeter 4a, carrying current I. The whole system is placed at frictionless horizontal surface in a uniform magnetic field →B=B0ˆj as shown in fig. In this situation, normal force between horizontal surface and block passes through a point at a distance x from center. Choose correct statement (s).
 AThe block must not topple if I<mgaB0BThe block must not topple if I<mg2aB0Cx=a4ifI=mg2aB0Dx=a4ifI=mg4aB0
AThe block must not topple if I<mgaB0BThe block must not topple if I<mg2aB0Cx=a4ifI=mg2aB0Dx=a4ifI=mg4aB0
A cubical block of mass M and edge a slides down a rougg inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has magnitude.
View SolutionA uniform cubical block of mass M and side length L is lying on the edge of a rough table with 14th of its edge overhanging. When a small block of mass m is placed on its top surface at the right edge (see fig.), the cube is on verge of toppling. The block of mass m is given a sharp horizontal impulse so that it acquires a velocity towards B. The small block moves on the top surface and falls on the other side. What is maximum coefficient of friction between the small block and the cube so that the cube does not rotate as the block moves over it. Assume that the friction between the cube and the table is large enough to prevent sliding of the cube on the table.

View SolutionIn a Young's interference experimental arrangement, the incident yellow light is composed of twpo wavelength 5890Å. The distance between of the two slits is 10−3m and screen is placed 1m away. Upto what order can frings be seen on the screen and how far from the centre of the screen does this occur?
View SolutionA rectangular tank having base 15cm×20cm is filled with water (density ρ=1000kg/m2) up to 20cm and force constant K=280N/m is fixed to the bottom of the tank so that the spring remains vertical.
This system is in an elevator moving downwards with acceleration a=2m/s2. A cubical block of side l=10cm and mass m=2kg is gently placed over the spring and released gradually, as shown in the figure.

a. Calculate compression of the spring in equilibrium position.
b. If the block is slightly pushed down from equilibrium position and released, calculate frequency of its vertical oscillations.
View SolutionConsider a two particle system with the particles having masses m1andm2. If the first particles pushed towards the centre of mass through a distance d, by what distance should the second particle be moved so as the keep the centre of mass at the same position?
View SolutionMolten lead of mass m=5.0g at a temperature t2=327∘C (the melting temperature of lead) was poured into a calorimeter packed with a large amount of ice at a temperature t1=0∘C. Find the entropy increment of the system lead-ice by the moment the thermal equilibrium is reached. The specific latent heat of melting of lead is equal to q=22.5J/g and its specific heat capacity is equal to c=0.125J/(g.K).
View SolutionThe figure shows a man of mass m standing at the end A of a trolley of maas M placed at rest on a smooth horizontal surface. The man starts moving towards the end B with a velocity urel with respect to the trolley. The length of the trolley is L.
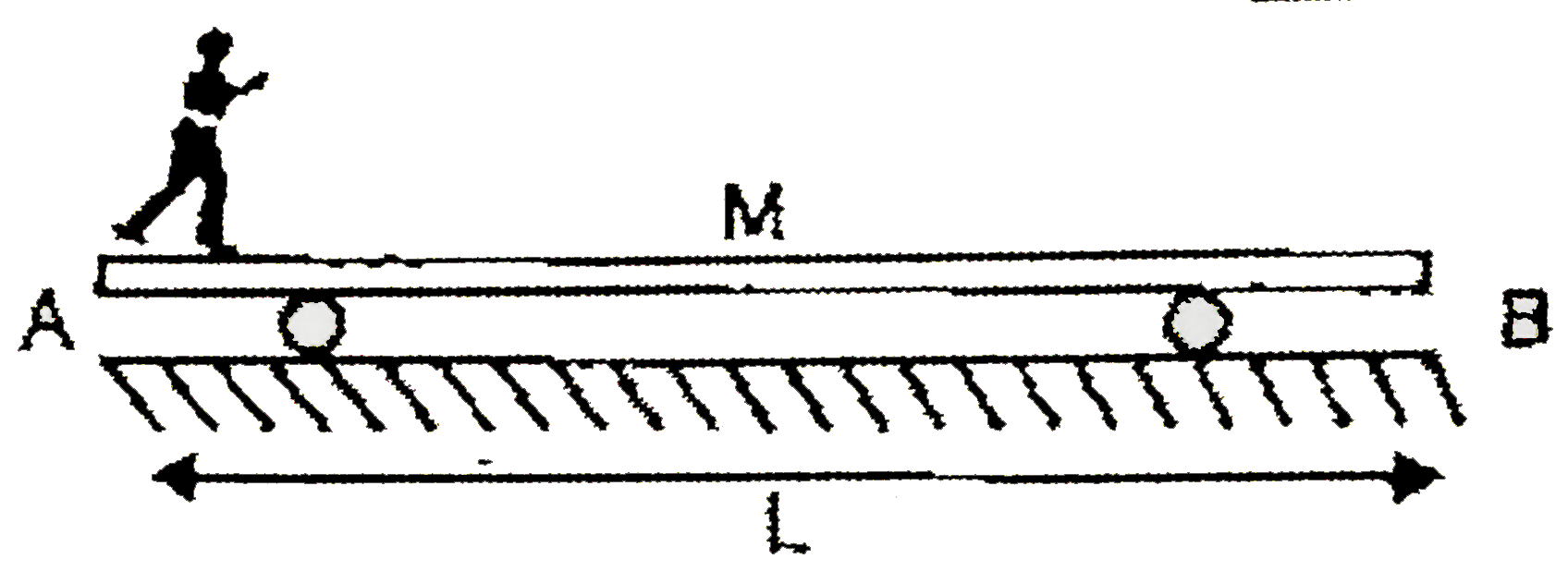
As the man walks on the trolley, the centre of mass of the system (man+ trolley) :
View Solution