A cubical block rests on an inclined plance of μ=1√3 . Determine the angle at which the block just slides down the incline .
To determine the angle at which a cubical block just starts to slide down an inclined plane with a coefficient of friction μ=1√3, we can follow these steps:
Step 1: Understand the Forces Acting on the Block
When the block is on the inclined plane, the forces acting on it are:
- The gravitational force →W=mg acting downwards.
- The normal force →N acting perpendicular to the surface of the incline.
- The frictional force →Ff acting up the incline, opposing the motion.
Step 2: Resolve the Gravitational Force
The weight of the block can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
Step 3: Write the Equation for Forces
At the angle of repose, the block is about to slide, so the frictional force equals the component of the weight acting down the incline:
Ff=W∥
The frictional force can be expressed as:
Ff=μN
Since the normal force N is equal to the perpendicular component of the weight:
N=W⊥=mgcosθ
Thus, we can write:
Ff=μ(mgcosθ)
Step 4: Set Up the Equation
At the point of impending motion, we have:
μ(mgcosθ)=mgsinθ
We can cancel mg from both sides (assuming mg≠0):
μcosθ=sinθ
Step 5: Substitute the Value of μ
Substituting μ=1√3:
1√3cosθ=sinθ
Step 6: Rearrange the Equation
Rearranging gives:
sinθcosθ=1√3
This can be expressed in terms of tangent:
tanθ=1√3
Step 7: Find the Angle
The angle whose tangent is 1√3 is:
θ=30∘
Conclusion
The angle at which the block just slides down the incline is 30∘.
---
When the block is on the inclined plane, the forces acting on it are:
- The gravitational force →W=mg acting downwards.
- The normal force →N acting perpendicular to the surface of the incline.
- The frictional force →Ff acting up the incline, opposing the motion.
The weight of the block can be resolved into two components:
- Perpendicular to the incline: W⊥=mgcosθ
- Parallel to the incline: W∥=mgsinθ
At the angle of repose, the block is about to slide, so the frictional force equals the component of the weight acting down the incline:
Ff=W∥
The frictional force can be expressed as:
Ff=μN
Since the normal force N is equal to the perpendicular component of the weight:
N=W⊥=mgcosθ
Thus, we can write:
Ff=μ(mgcosθ)
At the point of impending motion, we have:
μ(mgcosθ)=mgsinθ
We can cancel mg from both sides (assuming mg≠0):
μcosθ=sinθ
Substituting μ=1√3:
1√3cosθ=sinθ
Rearranging gives:
sinθcosθ=1√3
This can be expressed in terms of tangent:
tanθ=1√3
The angle whose tangent is 1√3 is:
θ=30∘
The angle at which the block just slides down the incline is 30∘.
Similar Questions
A frictionless inclined plane of length l having inclination θ is placed inside a lift which is accelerating downward with on acceleration a (<g). If a block is allowed to move down the inclined plane, from rest, then the time taken by the block to slide from top of the inclined plane to the bottom of the inclined plane is
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View Solution
Knowledge Check
A cubical block rests on a plane of μ=√3 . The angle through which the plane be inclined to the horizontal so that the block just slides down will be -
A30∘B45∘C60∘D75∘A cubical block rests on a plane of μ=√3 . The angle through which the plane be inclined to the horizontal so that the block just slides down will be -
A30∘B45∘C60∘D75∘A cubical block rests on an inclined plane of coefficient of friction μ=1√3 . What should be the angle of inclination so that the block just slides down the inclined plane?
A30∘B60∘C45∘D90∘
A block of mass m is placed on a rough inclined plane of inclination θ kept on the floor of the lift. The coefficient of friction between the block and the inclined plane is μ. With what acceleration will the block slide down the inclined plane when the lift falls freely ?
View SolutionA block has been placed on an inclined plane . The slope angle of θ of the plane is such that the block slides down the plane at a constant speed . The coefficient of kinetic friction is equal to :
View SolutionA block is placed on an inclined plane. The angle of inclination of the plane is such that the block slides down the plane at a constant speed. The coefficient of kinetic friction is
View Solution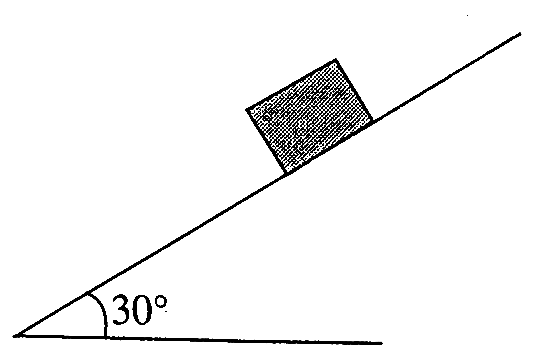
Figure shows a block kept on a rough inclined plane. The maximum external force down the incline for which the block remains at rest is 1 N while the maximum external force up the incline for which the block is at rest is 7 N. The coefficient of static friction μ is:
View SolutionA block of mass 10 kg is placed on an inclined plane when the angle of inclination is 30∘. The block just begins to slide down the plane. The force of static friction is
View Solution