A current carrying circular loop is placed in an infinite plane if ϕi is the magnetic flux through the inner region and ϕo is magnitude of magnetic flux through the outer region, then
ϕI>ϕo
ϕI<ϕo
ϕI=−ϕo
ϕI=ϕo
The correct Answer is:C
Step by step video, text & image solution for A current carrying circular loop is placed in an infinite plane if phi i is the magnetic flux through the inner region and phi o is magnitude of magnetic flux through the outer region, then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
A closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . Which of the following option is correct
 View Solution
View SolutionIn a coil of resistance 100Ω , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
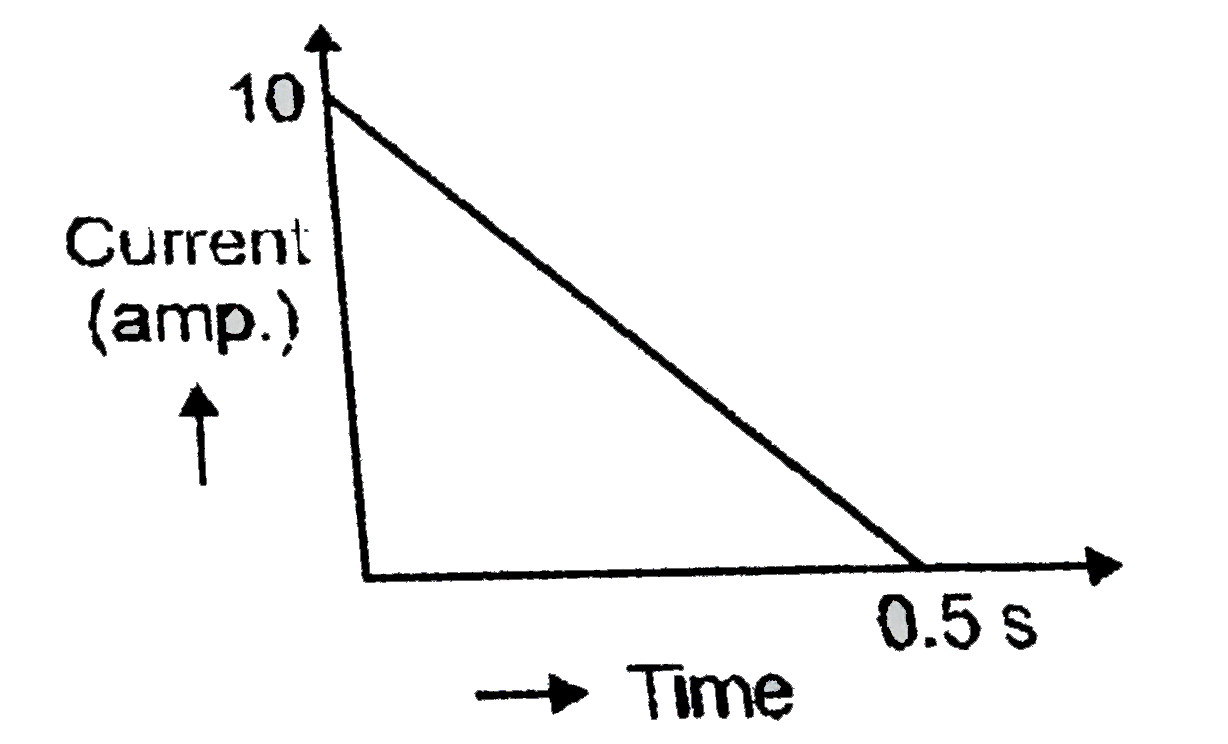 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A circular coil, carrying a constant current i s kept in the x - y plane. The magnetic flux through the entire x - y plane exluding the area of the circular coil is given by ϕ and the magetic flux through the area of the circular coil area is given by ϕ0, then
Aϕ>−ϕ0Bϕ<ϕ0Cϕ=−ϕ0Dϕ=ϕ0 - Question 2 - Select One
Consider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is phi _(0) then the magnetic flux through the other circular base will be:
Aϕ0B>ϕ0C−ϕ0D<ϕ0 - Question 3 - Select One
A circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
Adirectly proportional to IBdirectly proportional to RCinversly proportional to RDzero
A circular loop of radius 10 cm is placed in a region of magnetic field of 0.5 T with its plane parallel to the magnetic field. Calculate the magnetic flux through the coil.
View SolutionIn a coil of resistance 50 W, the induced current developed by changing magnetic flux through it, is shown in figure as a function of time. The magnitude of change in flux through the coil is
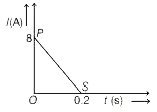 View Solution
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
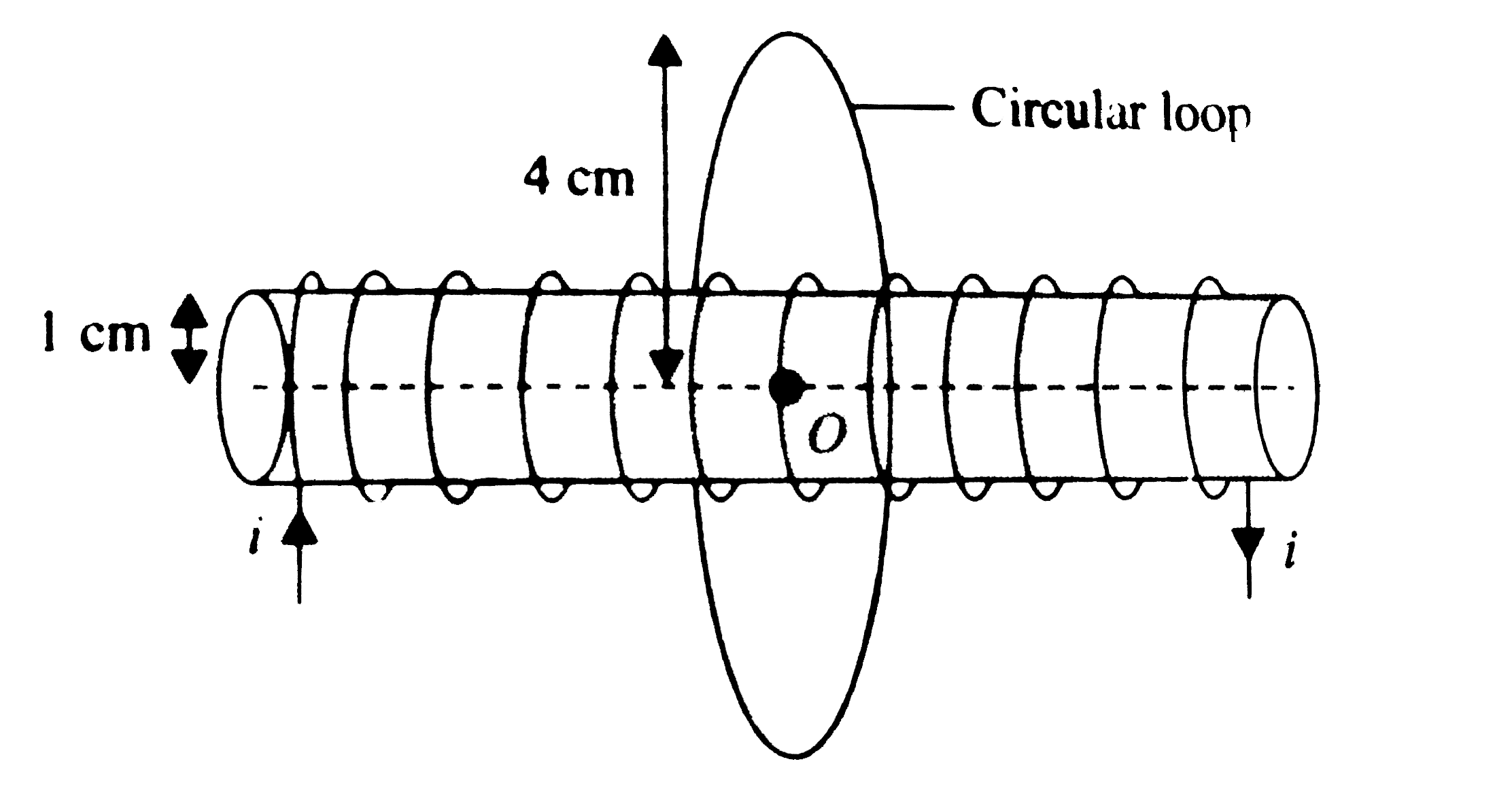
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.View SolutionA circular loop of radius r, carrying a current I lines in y - z plane with its centre at the origin. The net magnetic flux through the loop is
View SolutionA circular loop of radius R, carrying I lies in xy-plane with its centre at origin. The total magnetic flux through xy-plane is :
View Solution

