A long solenoid having n = 200 turns per metre has a circular cross-section of radius $a_{1} = 1 c m$ . A circular conducting loop of radius $a_{2} = 4 c m$ and resistance $R = 5 (Ω)$ encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

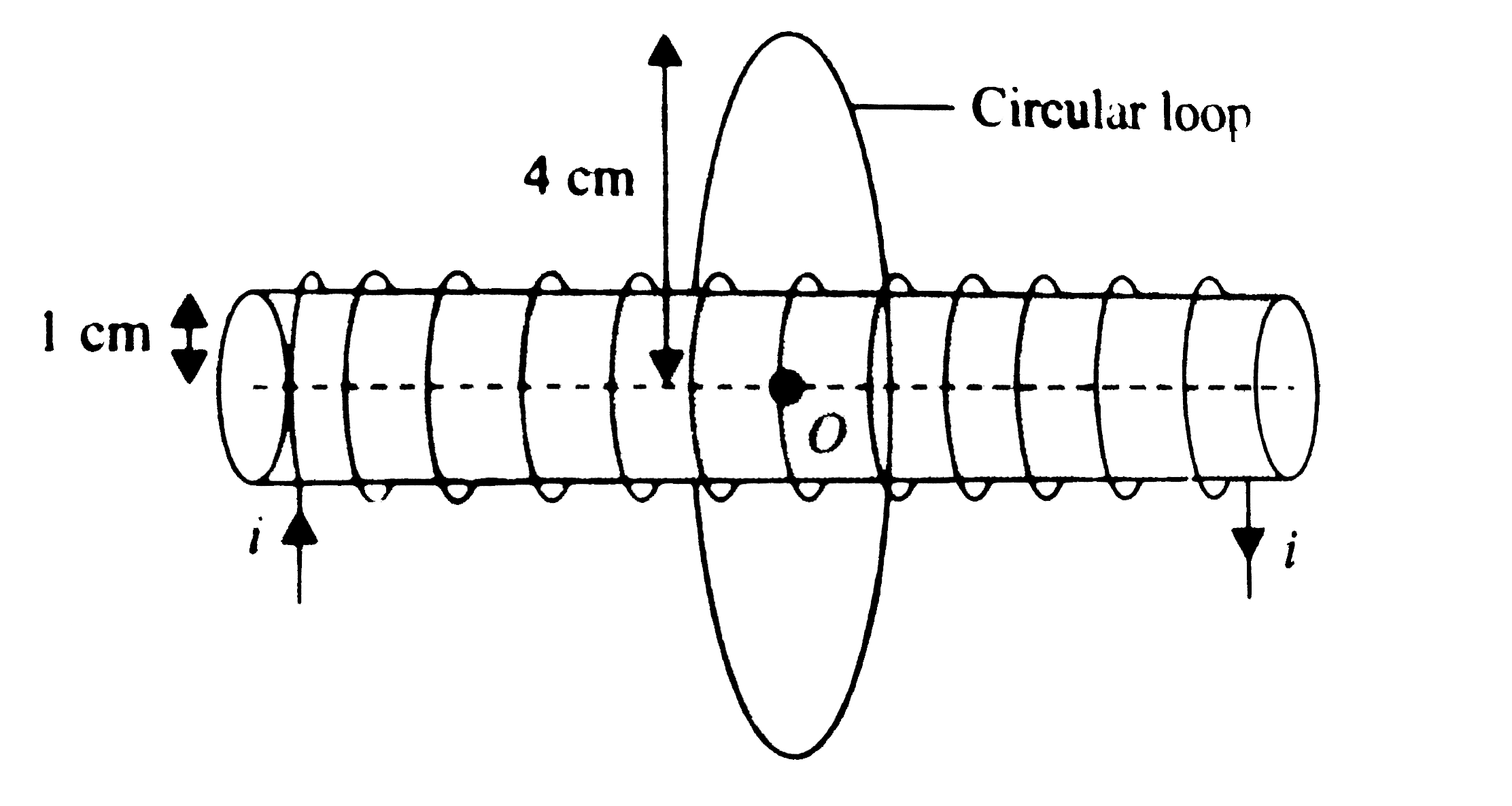
A current 't' in the solenoid results in magnetic field along its axis with magnitude $B = (μ) n i$ at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux ${(ϕ)}_{B}$ through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field $B = {(μ)}_{0} n i$ and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of $75 A / sec$ .
Magnetic of induced electric field strength in the circular loop is nearly We know that there is magnetic flux through the circular loop because of the magnetic field of current in the solenoid. For the purpose of circular loop, let us call it the external magnetic field. As current in the solenoid is reducing, external magnetic field for the circular loop also reduced resulting in induced current in the loop. Finally, as the solenoid current becomes zero, external field for the loop also becomes zero and stop changing. However, induced current in the loop will not stop at the instant at which the external field stops changing. This is because induced current itself produces a magnetic field that results in a flux through the loop. External field becoming zero without any further change will compel the induced current in the loop to become zero and so magnetic flux through the loop due to change in induced current will also change resulting in a further induced phenomenon that sustains currents in the loop even after the external field becomes zero.

$4.7 \times 10^{- 7} V m^{- 1}$

$3.82 \times 10^{- 6} V m^{- 1}$

$2.3 \times 10^{- 5} V m^{- 1}$

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

As found in privious part, the induced current is $i = 1.18 μ A$
Thus, induced voltage is $V = i R = 5.9 μ A$
Thus, magnitude of induced field stramgth in the circular loop is
$E = \frac{V}{2 π a_{2}} = 2.3 \times 10^{- 5} V / m$ .

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
A long solenoid having n = 200 turns per metre has a circular cross-section of radius $a_{1} = 1 c m$ . A circular conducting loop of radius $a_{2} = 4 c m$ and resistance $R = 5 (Ω)$ encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

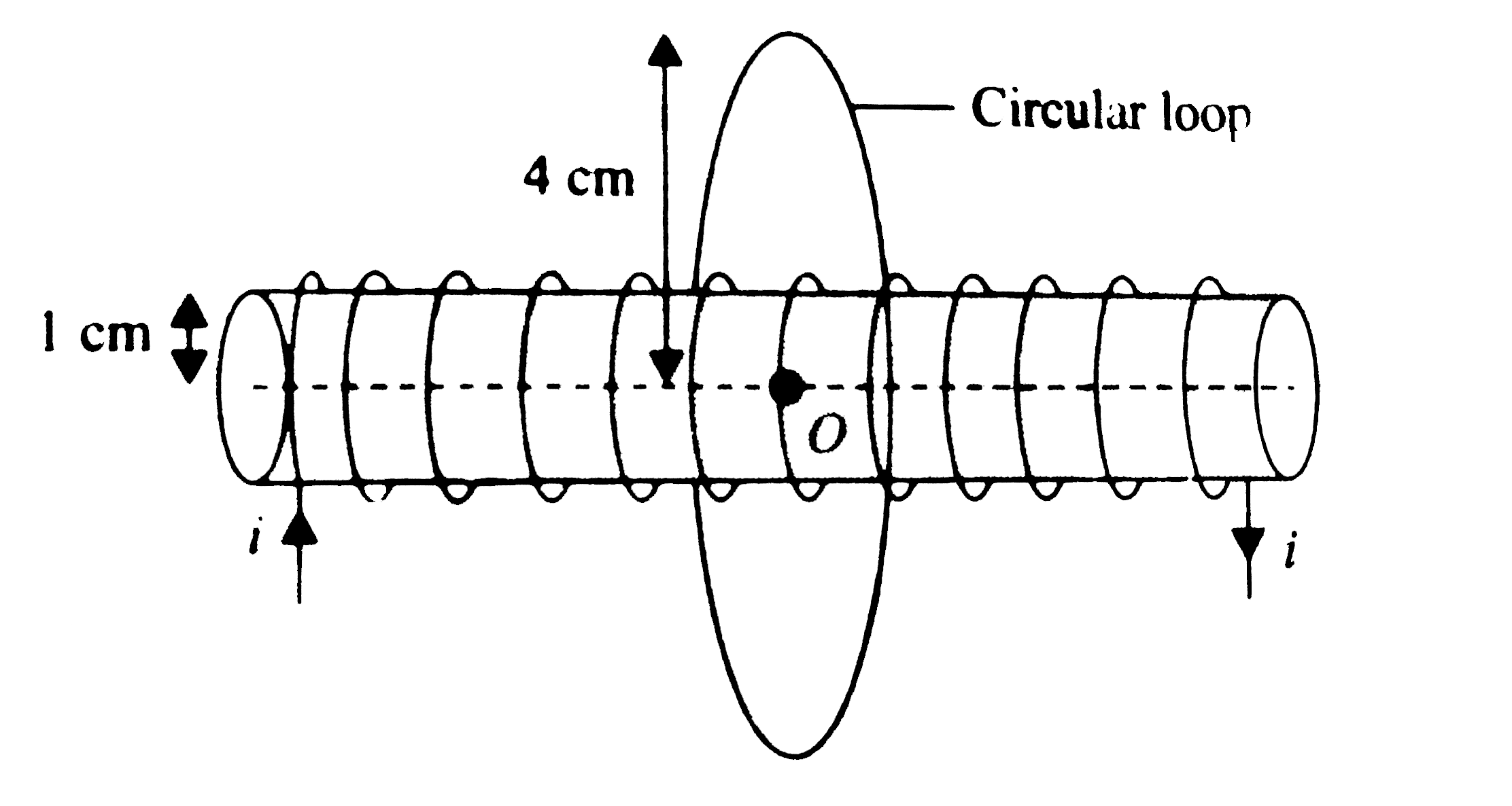
A current 't' in the solenoid results in magnetic field along its axis with magnitude $B = (μ) n i$ at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux ${(ϕ)}_{B}$ through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field $B = {(μ)}_{0} n i$ and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of $75 A / sec$ .
Magnitude of induced current that appears in the circular loop is
A $2.72 μ A$
B $1.18 μ A$
C $19.2 μ A$
DNone of these
Question 2 - Select One
A long solenoid having n = 200 turns per metre has a circular cross-section of radius $a_{1} = 1 c m$ . A circular conducting loop of radius $a_{2} = 4 c m$ and resistance $R = 5 (Ω)$ encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

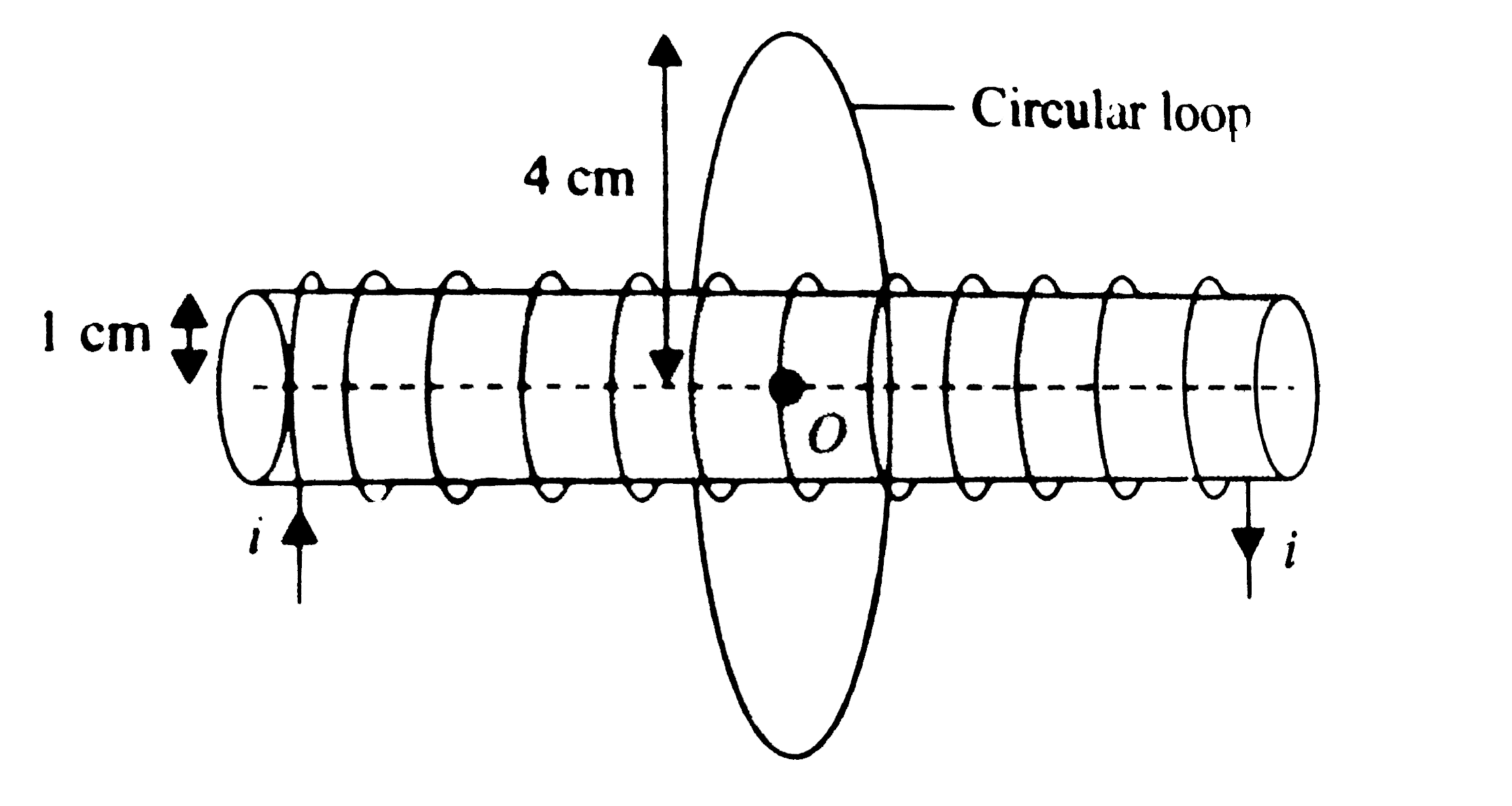
A current 't' in the solenoid results in magnetic field along its axis with magnitude $B = (μ) n i$ at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux ${(ϕ)}_{B}$ through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field $B = {(μ)}_{0} n i$ and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of $75 A / sec$ .
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
$a_{1}$ is the radius of solendoid and $a_{1} = 1 c m$ (given)
$a_{2}$ is the radius of circular loop and $a_{2} = 4 c m$ (given)
i is hte current in the solenoid
A $μ_{0} n i (π a_{1}^{2})$
B $μ_{0} n i (π a_{2}^{2})$
Czero
D $μ_{0} n i (π a_{1}^{2} + π a_{2}^{2})$
Question 3 - Select One
A long solenoid having n = 200 turns per metre has a circular cross-section of radius $a_{1} = 1 c m$ . A circular conducting loop of radius $a_{2} = 4 c m$ and resistance $R = 5 (Ω)$ encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

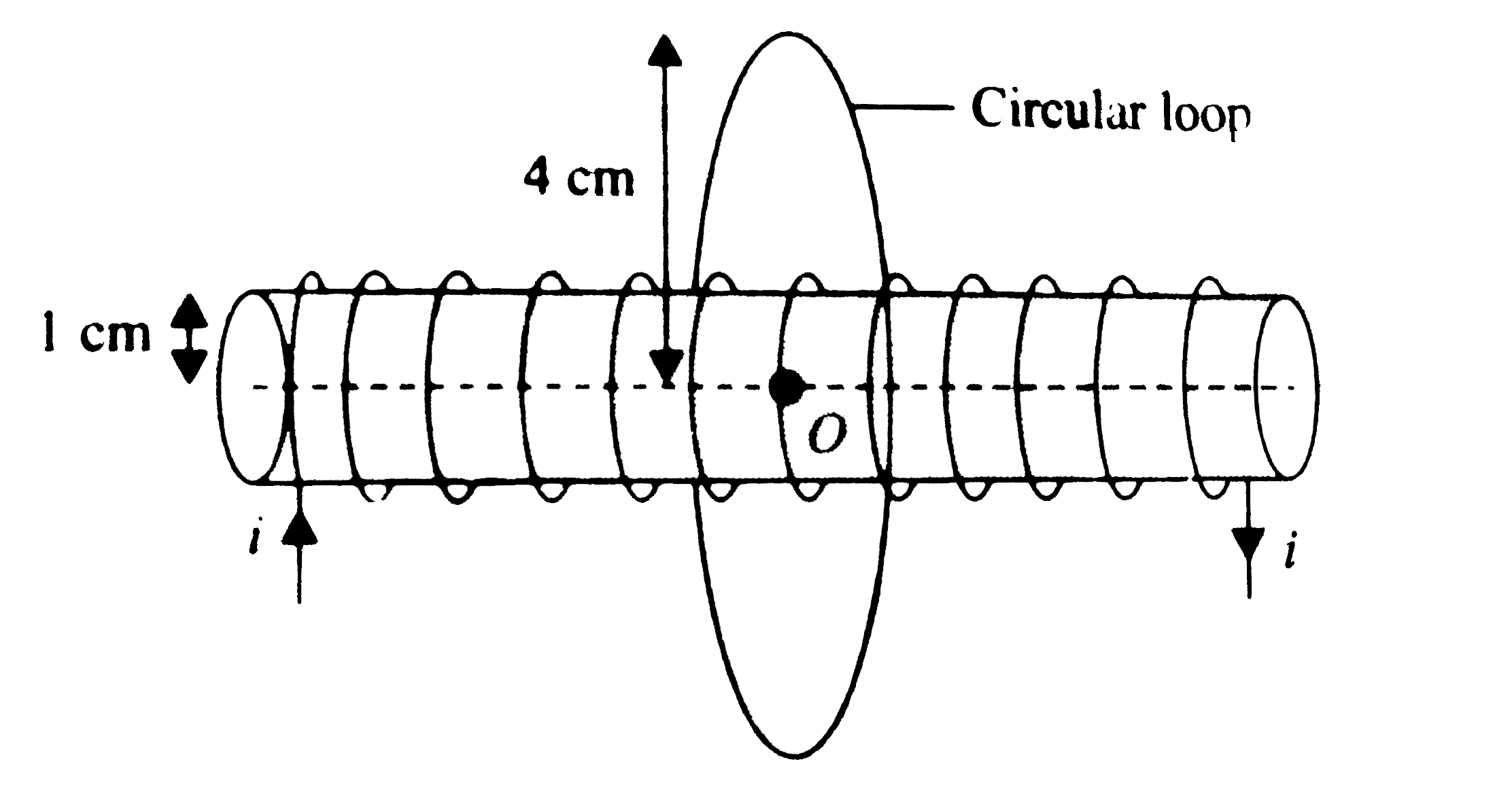
A current 't' in the solenoid results in magnetic field along its axis with magnitude $B = (μ) n i$ at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux ${(ϕ)}_{B}$ through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field $B = {(μ)}_{0} n i$ and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of $75 A / sec$ .
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
A $\frac{d I}{d t} = \frac{R}{μ_{0} n i} I$
B $\frac{d I}{d t} = - \frac{2 R}{π μ_{0} a_{2}} I$
C $\frac{d I}{d t} = - \frac{2 R}{μ_{0} a_{2}} I$
DNone of these