A current carrying circular loop of radius R is placed in the x-y plane with centre at the origin. Half of the loop with is now bent so that it now lies in the y-z plane.
The magnitude of magnetic moment now diminishes.
The magnetic moment does not change.
The magnitude of at increases.
The magnitude of at is unchanged.
The correct Answer is:A
To solve the problem, we need to analyze the situation of a current-carrying circular loop that is modified by bending half of it. We will calculate the magnetic moment before and after the modification.
1. Initial Setup:
- We have a circular loop of radius R lying in the x-y plane with its center at the origin. The current flowing through the loop is I.
2. Magnetic Moment of the Circular Loop in the x-y Plane:
- The magnetic moment m1 of a circular loop is given by the formula:
m1=I⋅A
- The area A of the circular loop is:
A=πR2
- Therefore, the magnetic moment in the x-y plane is:
m1=I⋅πR2
3. Modification of the Loop:
- Half of the loop (the part where x>0) is bent to lie in the y-z plane. This means we now have a semicircular loop in the y-z plane.
4. Magnetic Moment of the Semicircular Loop in the y-z Plane:
- The area of the semicircular loop is half of the full circular area:
A=12⋅πR2
- The magnetic moment m2 for the semicircular loop is:
m2=I⋅12⋅πR2
- Thus, we have:
m2=I⋅πR22
5. Direction of Magnetic Moments:
- The magnetic moment m1 (in the x-y plane) is directed along the z-axis (perpendicular to the plane).
- The magnetic moment m2 (in the y-z plane) is directed along the x-axis.
6. Calculating the Total Magnetic Moment:
- The total magnetic moment M can be found using the Pythagorean theorem since the two moments are perpendicular to each other:
M=√m21+m22
- Substituting the values:
M=√(I⋅πR2)2+(I⋅πR22)2
- Simplifying this:
M=√(I2⋅π2R4)+(I2⋅π2R44)
M=√I2⋅π2R4(1+14)=√I2⋅π2R4⋅54
M=I⋅πR2⋅√54=I⋅πR2⋅√52
7. Conclusion:
- The total magnetic moment M is less than the initial magnetic moment m1. Therefore, we can conclude that the magnetic moment diminishes after bending half of the loop.
- We have a circular loop of radius R lying in the x-y plane with its center at the origin. The current flowing through the loop is I.
- The magnetic moment m1 of a circular loop is given by the formula:
m1=I⋅A
- The area A of the circular loop is:
A=πR2
- Therefore, the magnetic moment in the x-y plane is:
m1=I⋅πR2
- Half of the loop (the part where x>0) is bent to lie in the y-z plane. This means we now have a semicircular loop in the y-z plane.
- The area of the semicircular loop is half of the full circular area:
A=12⋅πR2
- The magnetic moment m2 for the semicircular loop is:
m2=I⋅12⋅πR2
- Thus, we have:
m2=I⋅πR22
- The magnetic moment m1 (in the x-y plane) is directed along the z-axis (perpendicular to the plane).
- The magnetic moment m2 (in the y-z plane) is directed along the x-axis.
- The total magnetic moment M can be found using the Pythagorean theorem since the two moments are perpendicular to each other:
M=√m21+m22
- Substituting the values:
M=√(I⋅πR2)2+(I⋅πR22)2
- Simplifying this:
M=√(I2⋅π2R4)+(I2⋅π2R44)
M=√I2⋅π2R4(1+14)=√I2⋅π2R4⋅54
M=I⋅πR2⋅√54=I⋅πR2⋅√52
- The total magnetic moment M is less than the initial magnetic moment m1. Therefore, we can conclude that the magnetic moment diminishes after bending half of the loop.
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - ASSERTION & REASON15videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - Magnetic Force15videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISM EXERCISE - HOTS5videos
MOVING CHARGES AND MAGNETISM
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - NCERT Exemplar5videos
MAGNETISM AND MATTER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - NUCLEIEXERCISE - Assertion And Reason15videos
NUCLEI
Similar Questions
A current − carrying circular loop of radius R is placed in the XY− plane with centre at the origin. Half of the loop with x>0 is now bent so that is now lies in the YZ− plane
View SolutionA circular wire loop of radius R is placed in the X-Y plane with its centre at the origin. The loop carries a current I in the clockwise direction when viewed from a point on the positive Z-axis. A uniform magnetic field →B=B0(ˆi+√3ˆj2) exists in the region x>R√32. The magnitued of the magnetic force on the loop due to the magnetic field is B0IRn. The value of n is______________.
View SolutionA circular wire loop of radius R is placed in the x-y plane centered at the origin O. A square loop of side a(altltR) having two turns is placed with its centre at =√3R along the axis of hte circular wire loop, as shown in figure. The plane of the square loop makes an angle of 45∘ with respect to the z-axis. If the mutual inductance between the loops is given bu μ0a22p/2R, then the value of p is
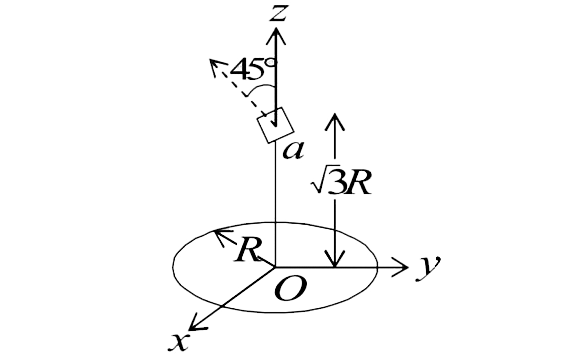 View Solution
View SolutionA circular wire loop of radius R is placed in the x-y plane centered at the origin O. A square loop of side a(altltR) having two turns is placed with its centre at =√3R along the axis of hte circular wire loop, as shown in figure. The plane of the square loop makes an angle of 45∘ with respect to the z-axis. If the mutual inductance between the loops is given bu μ0a22p/2R, then the value of p is
 View Solution
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
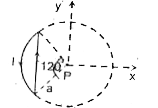 View Solution
View SolutionA current carrying circular loop is freely suspended by a long thread. The plane of the loop will point in the direction
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA current carrying circular loop of radius R is placed in a uniform magnetic field B0 Tesla in x-y plane as shown in figure. The loop carries a current i=1A in the direction shown. Find the torqure acting on the loop
View SolutionA current carrying loop lies on a smooth horizontal plane. Then,
View Solution

