A current I flows along a round loop. Find the integral ∫→B.→dr along the axis of the loop within the range from (−∞) to (+∞). Explain the result obtained.
The magnetic field at point P on the axis of a coil at distance
from the centre of the coil is
Bx=μ0IR22(R2+x∘)3/2
the axis of the loop is taken along the x-axis.
∫+∞−∞→B.→dr=∫+∞−∞Bxdx=μ0IR22∫+∞−∞dx(R2+x2)3/2
=μ0IR22∫π/2−π/2Rsec2θR3sec3θ=μ0I2∫π/2−π/2cosθdθ=μ0I

The integral on the LHS can be thought of as the line integral of
B over a closed path (a straight line from (−∞) to (+∞) and a semi-
circle of infinite radius where the magnetic field vanishes). Then
as per Amper's law, this must be μ0 times the current enclosed
by the path which is I.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.135videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - Concept Exercise 2.210videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type12videos
SOURCES OF MAGNETIC FIELD
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.612videos
RAY OPTICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Comprehension Type14videos
WAVE OPTICS
Similar Questions
A current I flows along a round circular loop of radius R. Find the line integration of magnetic field along the axis of the loop from center to ∞
View SolutionA current I flows along a triangle loop having sides of equal length a. The strength of magnetic field at the centre of the loop is :
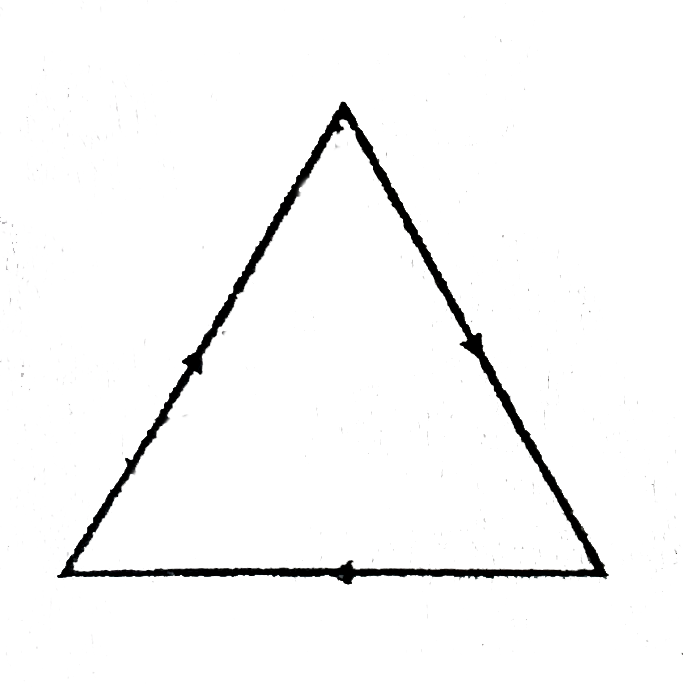 View Solution
View SolutionA: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.View SolutionA current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor fo the cable, then the magnetic induction at any point outside the conductor at a distance r metre from the axis is
View SolutionFigure. shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop,
a. find the mutual inductance of the two coils,
b. find the emf induced in the larger coil,
c. if the resistance of the larger loop is R, find the current in it as a function of time.
 View Solution
View SolutionFigure shows two concentric coplanar coils with radii a and b(a<<b). A current I=2t flows in the smaller loop. Neglecting self-inductance of the larger loop,
a. find the mutual inductance of the two coils,
b. find the emf induced in the larger coil,
c. if the resistance of the larger loop is R, find the current in it as a function of time.
 View Solution
View SolutionA current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
View SolutionA current I amperes flows through a loop abcdefgha along the edge of cube of width l metres as shown in figure. One corner 'a' of the loop lies at origin.

This current path (abcdefgha) can be trated as a superposition of three square loops carrying current I Choose the correct option ?View SolutionA current I amperes flows through a loop abcdefgha along the edge of cube of width l metres as shown in figure. One corner 'a' of the loop lies at origin.

The unit vector in the direction of magnetic field at the centre of cube abcdefgh of width l is given byView SolutionThe figure shows a circular loop of radius a with two long parallel wires (νmbered1and2) all in the plane of the paper . The distance of each wire from the centre of the loop is d. The loop and the wire are carrying the same current I. The current in the loop is in the counterclockwise direction if seen from above.
(q) The magnetic fields(B) at P due to the currents in the wires are in opposite directions.
(r) There is no magnetic field at P.
(s) The wires repel each other.
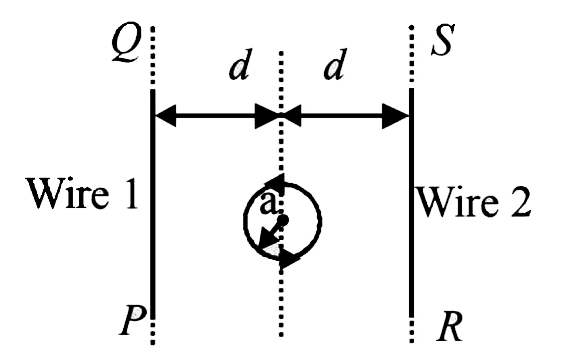
(4) When d≈a but wires are not touching the loop , it is found that the net magnetic field on the axis of the loop at a height h above the loop is zero. In that caseView Solution

