A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic field induction at the center of polygon due to one side of the polygon is
A
B
C
D
Video Solution
Text Solution
The correct Answer is:C
But
or
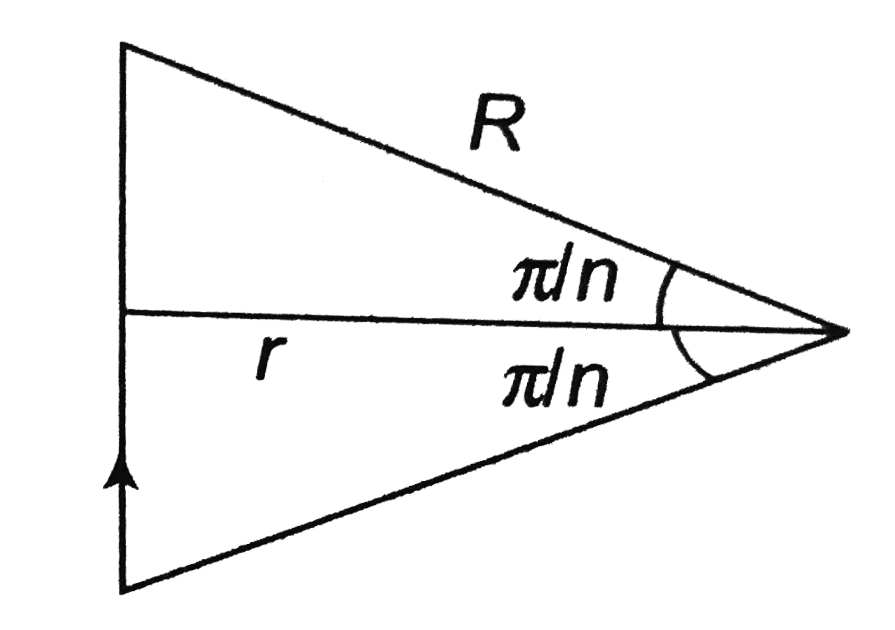
or
|
Topper's Solved these Questions
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Magnetic Field Due To Circular Arc
Explore 69 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Problems Based On Mixed Concepts
Explore 32 Videos
- SOURCE AND EFFECT OF MAGNETIC FIELDBook:A2ZChapter:SOURCE AND EFFECT OF MAGNETIC FIELDExercise:Magnetic Dipole
Explore 32 Videos
- SEMICONDUCTOR ELECTRONICSBook:A2ZChapter:SEMICONDUCTOR ELECTRONICSExercise:EXERCISE
Explore 29 Videos
- WAVE OPTICSBook:A2ZChapter:WAVE OPTICSExercise:Section D - Chapter End Test
Explore 29 Videos
Similar Questions
Knowledge Check
A current I flows through a thin wire shaped as regular polygon of n sides which can be inscribed in a circle of radius R. The magnetic fidl induction at the center of polygon due to one side of the polygon is
Aμ0IπR(tanπn)Bμ0I4πRtanπnCμ0I2πR(tanπn)Dμ0I2πR(cosπn)In the following figure a wire bent in the form of a regular polygon of n sides is inscribed in a circle of radius a. Net magnetic field at centre will be
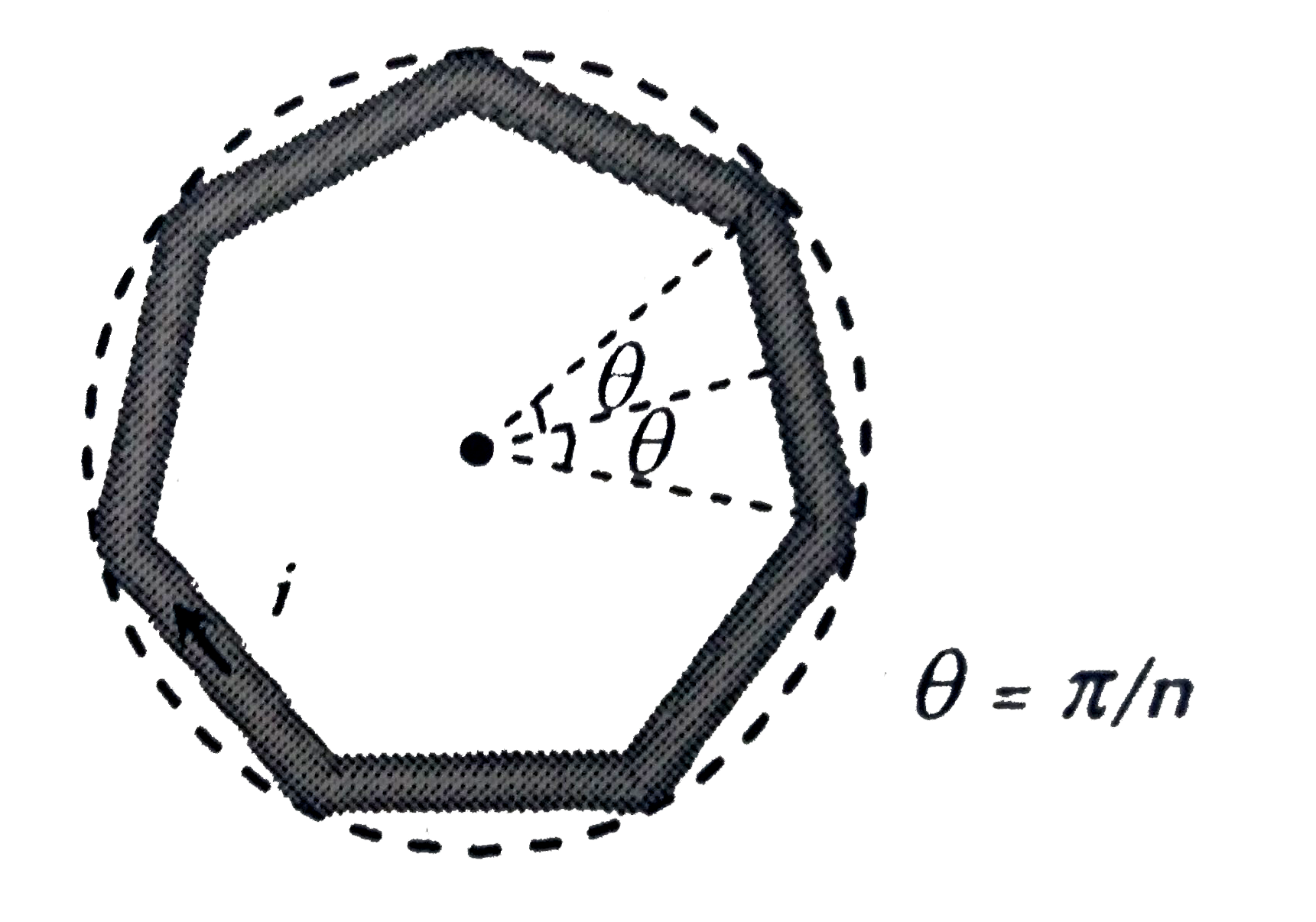 Aμ0i2πatanπnBμ0ni2πatanπnC2πniaμ0tanπnDni2aμ0tanπn
Aμ0i2πatanπnBμ0ni2πatanπnC2πniaμ0tanπnDni2aμ0tanπnA current I flows in a thin wire in the shape of a regular polygon n sides. The magnetic induction at the centre of the polygon when n→∞ is (R is the radius of its circumcircle)
Aμ0ni2πRtanπ6Bμ0ni2πRtanπRCμ0i2RDzero
A regular polygon of 9 sides where length of each side is 2 is inscribed in a circle. Then the radius of the circle is
View SolutionIf a twelve sides regular polygon is inscribed in a circle of radius 3 centimeters, then the length of each side of the polygon is
View SolutionIf a regular polygon of n sides has circum radius R and inradius r then each side of polygon is:
View SolutionThe limit of the interior angle of a regular polygon of n sides as n→∞ is
View SolutionIf a thin wire of length L is given the shape of a regular polygon of n sides and current I flows through it, what will be the net magnetic field at the centre of the polygon if n is infinity?
View Solution