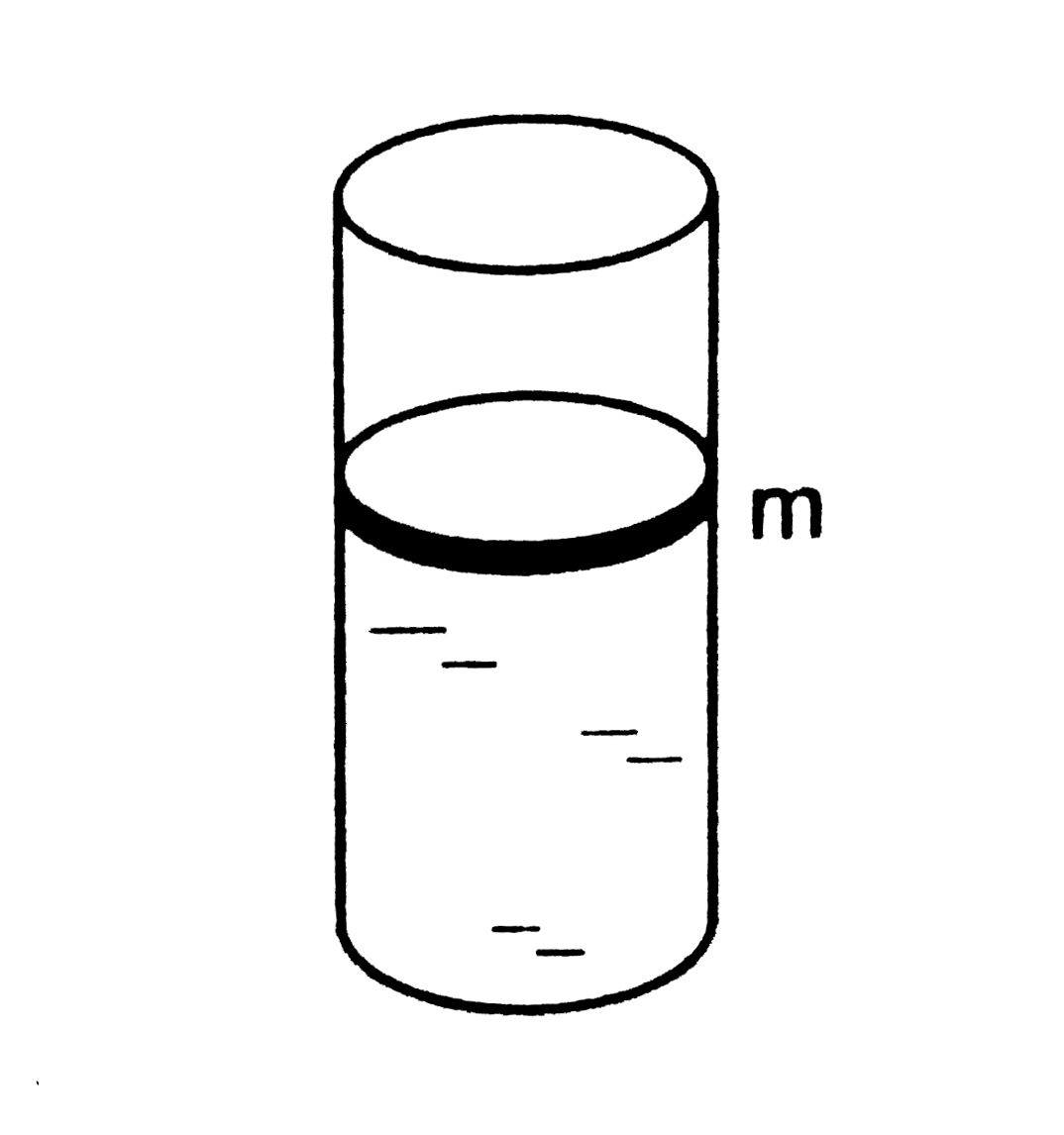
A cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
The correct Answer is:A
Let the pressure of the liquid just below the piston be p. The force acting on the piston are:
(a) its weight, mg(downwards)
(b) force due to the air above it, p0A(downwards)
(c ) Force due to the liquid below it, pA(upwards)
It the piston is in equilibrium,
pA=p0A+mg
or, p=p0+mgA.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Introductory Exercise
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.2
2 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Miscellaneous Examples
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A cylindrical vessel containing a liquid is closed by a smooth piston of mass "100g" as shown in the figure.The radius of the piston is "10cm" .If the atmospheric pressure is P0 then the pressure difference of the liquid just below the piston and the atmospheric pressure is (g=10ms2)
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View Solution
Knowledge Check
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgA
A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgAA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA)
A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA)An ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass M. The piston and the cylinder have an equal cross-sectional area A. Atmospheric pressure is p0 and when the piston is in equilibrium, the volume of the gas is V0. The piston is now displaced slightly from its equilibrium position. Assuming that the system, is completely isolated from, its surroundings, what is the frequency of oscillation.
Af=12π√γ(p0A2+MgA)V0MBf=12π√1γ(p0A2+MgA)V0MCf=12π√(p0A2+MgA)V0MDf=12π√A(p0A2+MgA)V0M
A cylinder vessel containing a liquid of density ρ is closed by a smooth piston of mass m as shown. If atmospheric pressure is P0, radius of cylinder is r and height of liquid is h. Find
(a) Pressure of liquid just below the piston
(b) force at bottom of cylinder.
 .
.
View SolutionAn ideal gas enclosed in a cylindrical container supports a freely moving piston of mass M. The piston and the cylinder have equal cross-sectional area A. When the piston is in equilibrium, the volume of the gas is V0 and its pressure is P0. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
View SolutionWhen a pressure measuring device is immersed in a liquid, a restoring force of 2 N is exerted by the spring. If the area of cross-section of the pistion is 10 cm2, what pressure does the fluid exert on the piston?
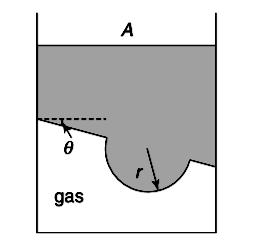
View SolutionAn ideal gas is enclosed in a cylinder having cross sectional area A. The piston of mass M has its lower face inclined at θ to the horizontal. The lower face of the piston also has a hemispherical bulge of radius r. The atmospheric pressure is P0.
(a) Find pressure of the gas.
(b) The piston is slowly pulled up by a distance x. During the process the piston is always maintained in equilibrium by adding heat to the gas. [It means if the piston is left at any stage it will stay there in equilibrium]. Find change in temperature of the gas. Number of mole of the gas in the cylinder is one.
View SolutionA rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)

View Solution
