A cylinder vessel containing a liquid of density ρ is closed by a smooth piston of mass m as shown. If atmospheric pressure is P0, radius of cylinder is r and height of liquid is h. Find
(a) Pressure of liquid just below the piston
(b) force at bottom of cylinder.
 .
.
(a) Forces acting on piston
(i) weight of piston, mg (downward)
(ii) force due to air above it, P0A (downward)
(iii) force due to liquid below it, PA (upward)
If the piston is in equilibrium
PA=P0A+mg
P=P0+mgA=P0+mgπr2
(b) Pressure at bottom of cylinder
P'=P0+mgπr2+ρgh
Force at bottom of cylinder
F=P'πr2=(P0+mgπr2+ρgh)πr2.
Topper's Solved these Questions
Similar Questions
A cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA cylinderical vessel contaning liquid is closed by a smooth piston of mass m. the area of cross-section of the piston is A. if the atmospheric pressure is P0, Find the pressure of the liquid just below the piston.
View Solution
Knowledge Check
A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA)
A√2ghB√2(gh+mgρA)C√2(gh+mgA)D√2(gh+mgA)A cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is
 A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgA
A√2ghB√2(gh+mgpA)C√2(gh+mgA)D√2gh+mgA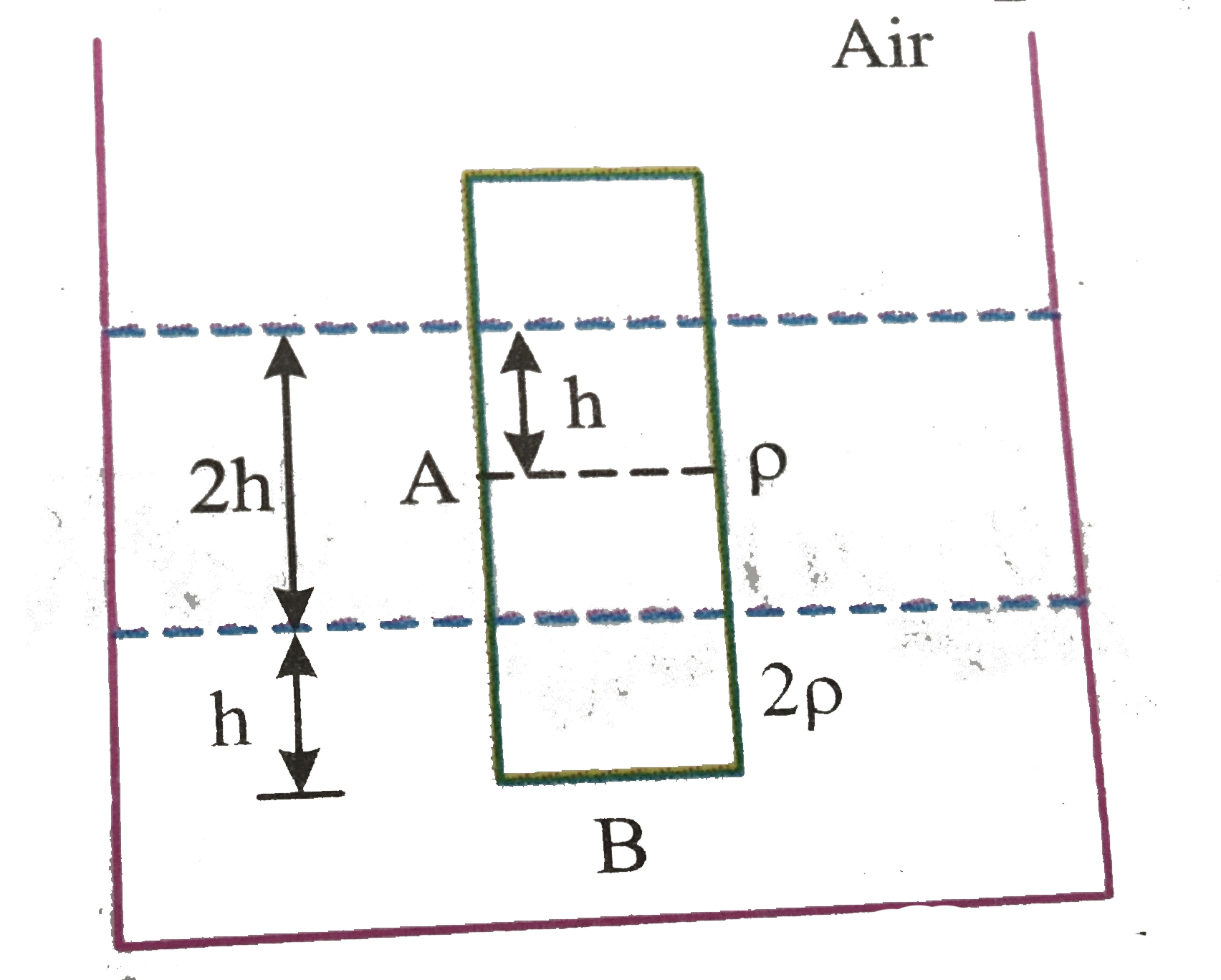
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:A2πghB3ρghC4ρghDnone
A cylindrical vessel containing a liquid is closed by a smooth piston of mass "100g" as shown in the figure.The radius of the piston is "10cm" .If the atmospheric pressure is P0 then the pressure difference of the liquid just below the piston and the atmospheric pressure is (g=10ms2)
View SolutionFind height of liquid in container when observer in air observes that height of liquid is half of actual height of cylinder.
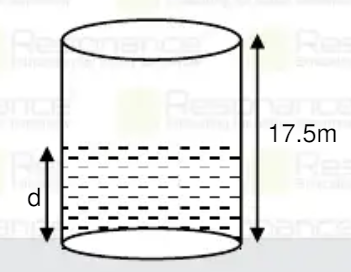
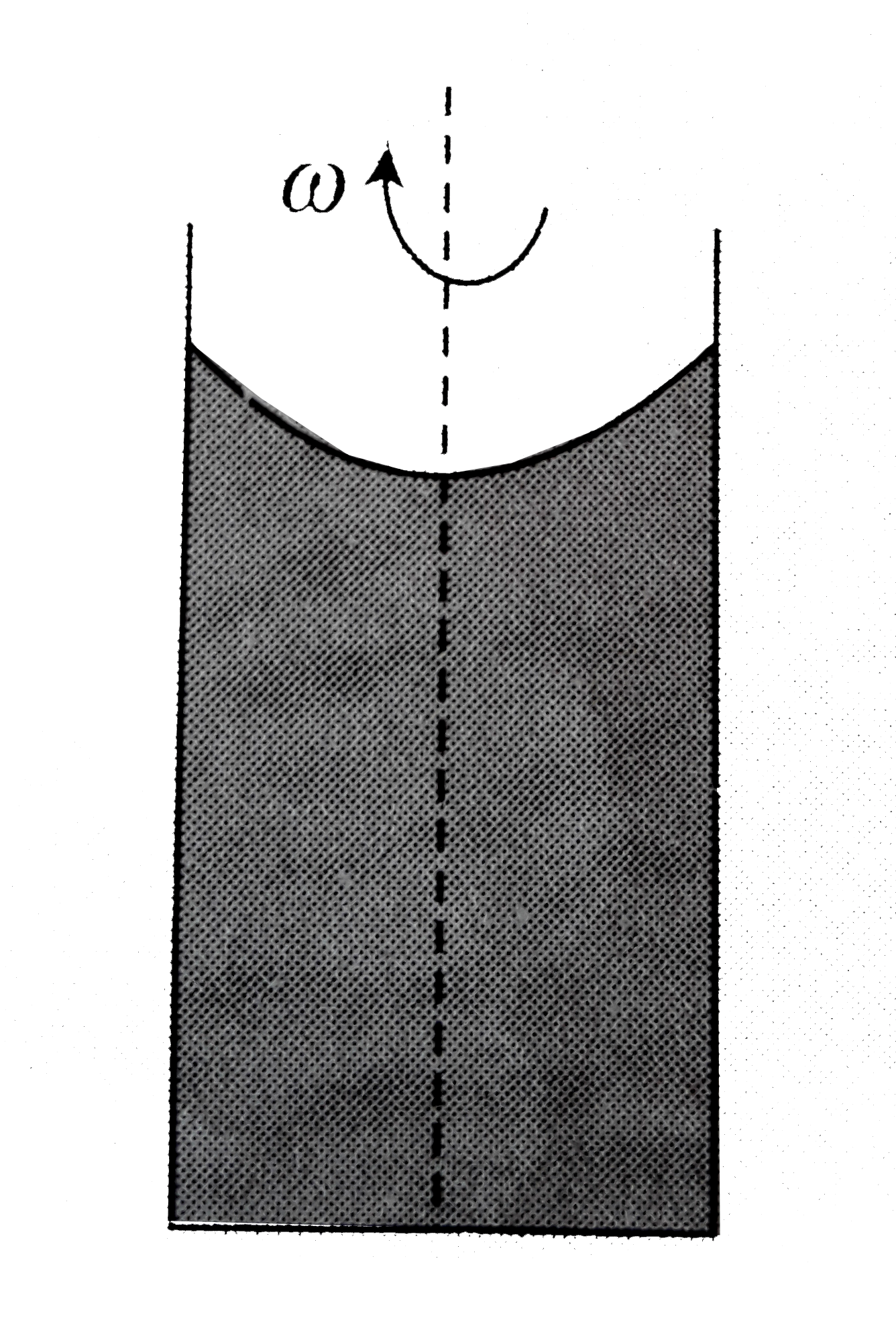
View SolutionA cylinder of radius R full of liquid of density p is rotated about its axis at w rad/s. The increase in pressure at the centre of the cylinder will be
View SolutionA liquid of density ρ is in a vessel rotating with angular velocity ω as shown in figure. If P0 is the atmospheric pressure, find pressure at a radial distance r from the axis.
 .
.
View SolutionA liquid of density ρ is filled in a beaker of cross section A to a height H and then a cylinder of mass M and cross-section a is made to float in it as shown in

If the atmospheric pressure is P0 find the pressure (a) at the top face B of the cylinder (b) at the bottom face C of the cylinder and (c ) at the base D of the beaker. (d) Can ever these pressure be equal ?
View Solution
