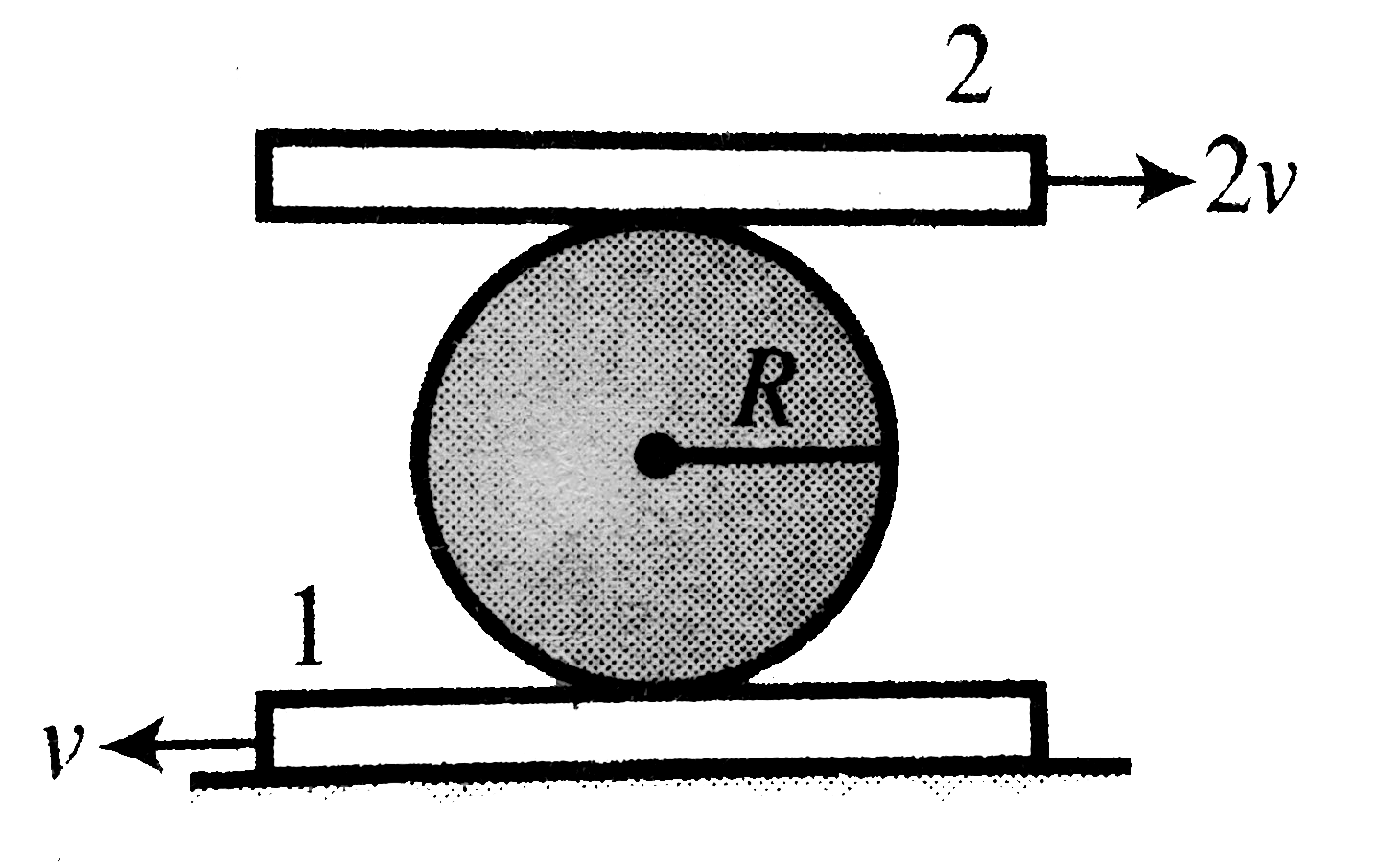
A cylinder is rolling without sliding over two horizontal planks (surfaces) and . If the velocities of the surfaces and are and respectively, find the:
a. Position of instantaneous axis of rotation.
b. Angular velocity of the cylinder.
The correct Answer is:
a. Since there is no relative sliding between the cylinder and the planks and , the points, and of the disc will move with velocities equal to the velocities of the respective surface.
and
respectively. Joining and and and we find the point as . Then we have the similar triangles and . Using the properties of similar triangles we have

and
Then we have
This gives,
hence is located at a distance of below the top of the disc.
b. As we know
and
This gives clockwise
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct
97 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.4
11 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
A disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

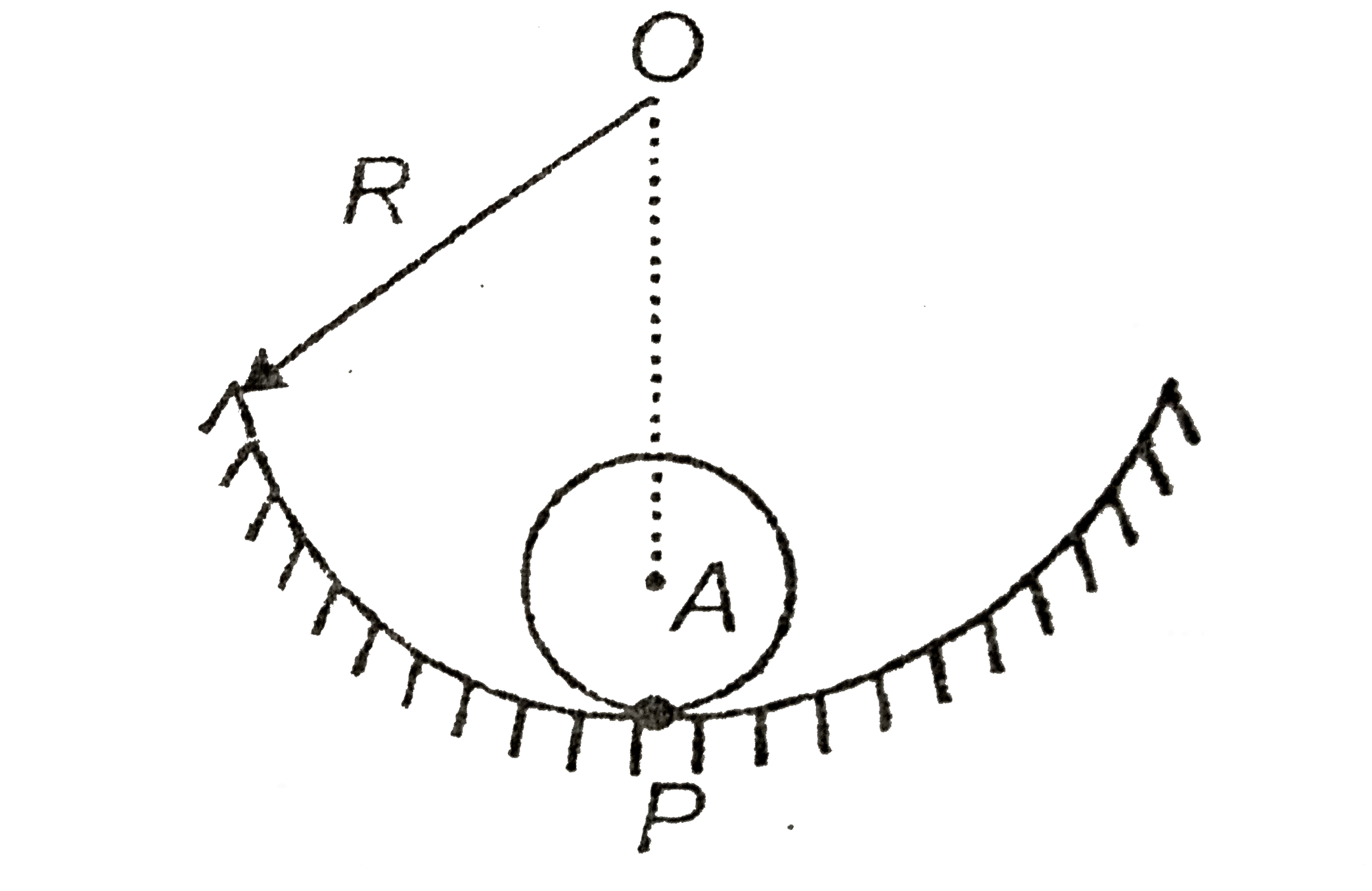
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
View SolutionA uniform disc of radius R rolls perfectly over two horizontal plank A and B moving with velocities v and 2v, spectively. Find the
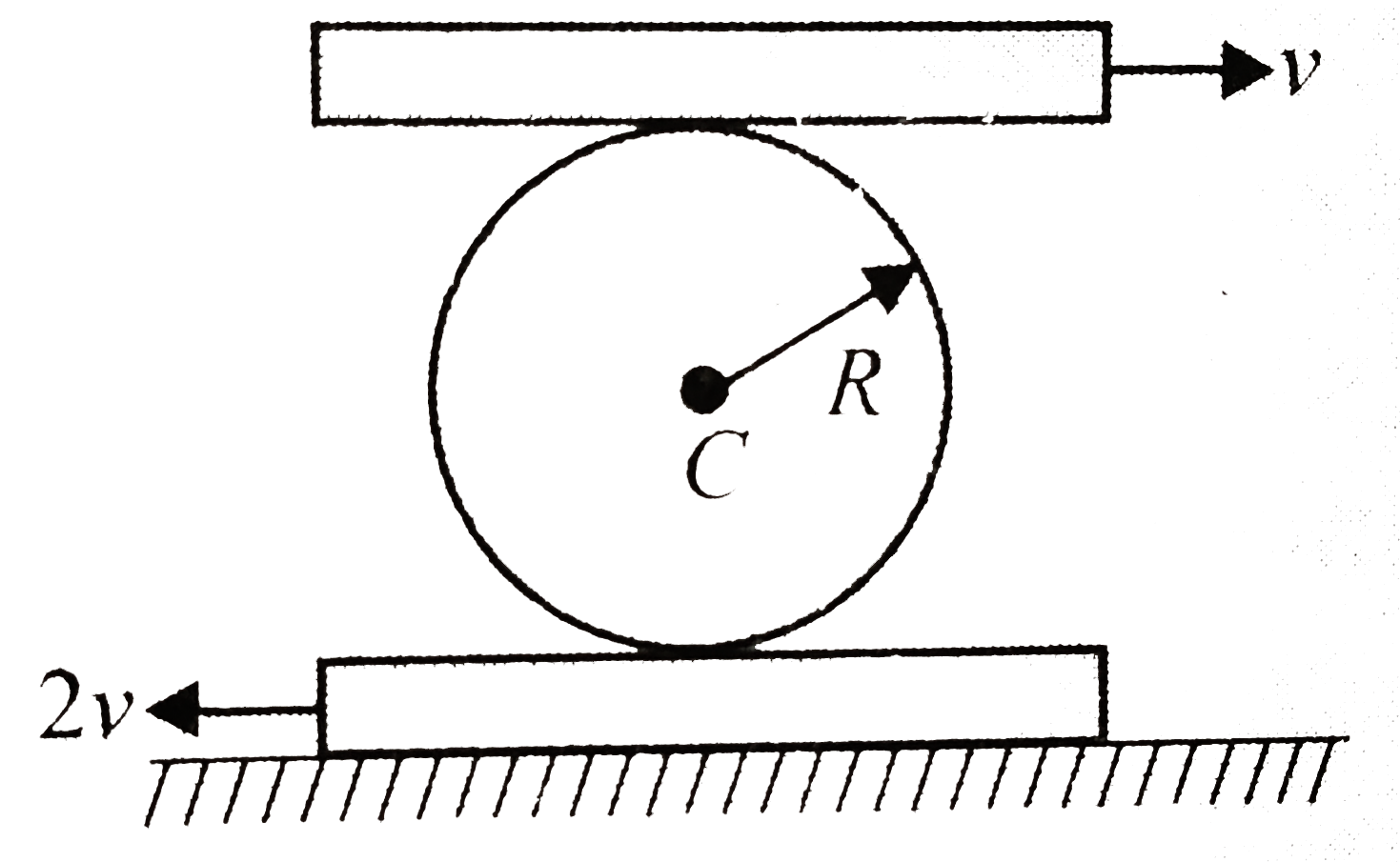
a. velocity of CM of the disc.
b. angular velocity of the disc.
View SolutionTwo bodies have their moments of inertia I and 2I, respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
View Solution
A disc is rolling without slipping with linear velocity v as shown in figure. With the concept of instantaneous axis of rotation, find velocities of point A, B, C and D.
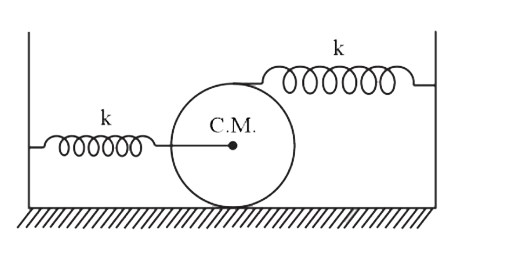
View SolutionA uniform solid cylinder can roll without sliding on a horizontal surface as shown in the figure. The mass of cylinder is 10 kg and the spring constant for both the ideal springs is 300Nm−1 . What is the angular frequency (in rad s−1 ) of small oscillations of the centre of the cylinder?
View SolutionA uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View SolutionA disc of the radius R is confined to roll without slipping at A and B. If the plates have the velocities v and 2v as shown, the angular velocity of the disc is

View SolutionA bullet of mass m moving with a velocity of u just grazes the top of a solid cylinder of mass M and radius R resting on a rough horizontal surface as shown and is embedded in the cylinder after impact. Assuming that the cylinder rolls without slipping, find the angular velocity of the cylinder and the final velocity of the bullet.

View SolutionA cylinder of water, is rotating about its own axis with uniform angular velocity ω. The shape of free surface of water will be
View Solution
