A block of mass M=4kg of height and breath b is placed on a rough plank of same mass M. A light inextensible string is connected to the upper end of the block and passed through a light smooth pulley as shown in figure. A mass m=1kg is hung to the other end of the string.
a. What should be the minimum value of coefficient of friction between the block and the plank so that, there is no slipping between the block and the wedge?
b. Find the minimum value of b/h so that the block does not topple over the plank, friction is absent between the plank and the ground.

The correct Answer is:4/9
Drawing free body diagram of all the three (blocks plank and mass)
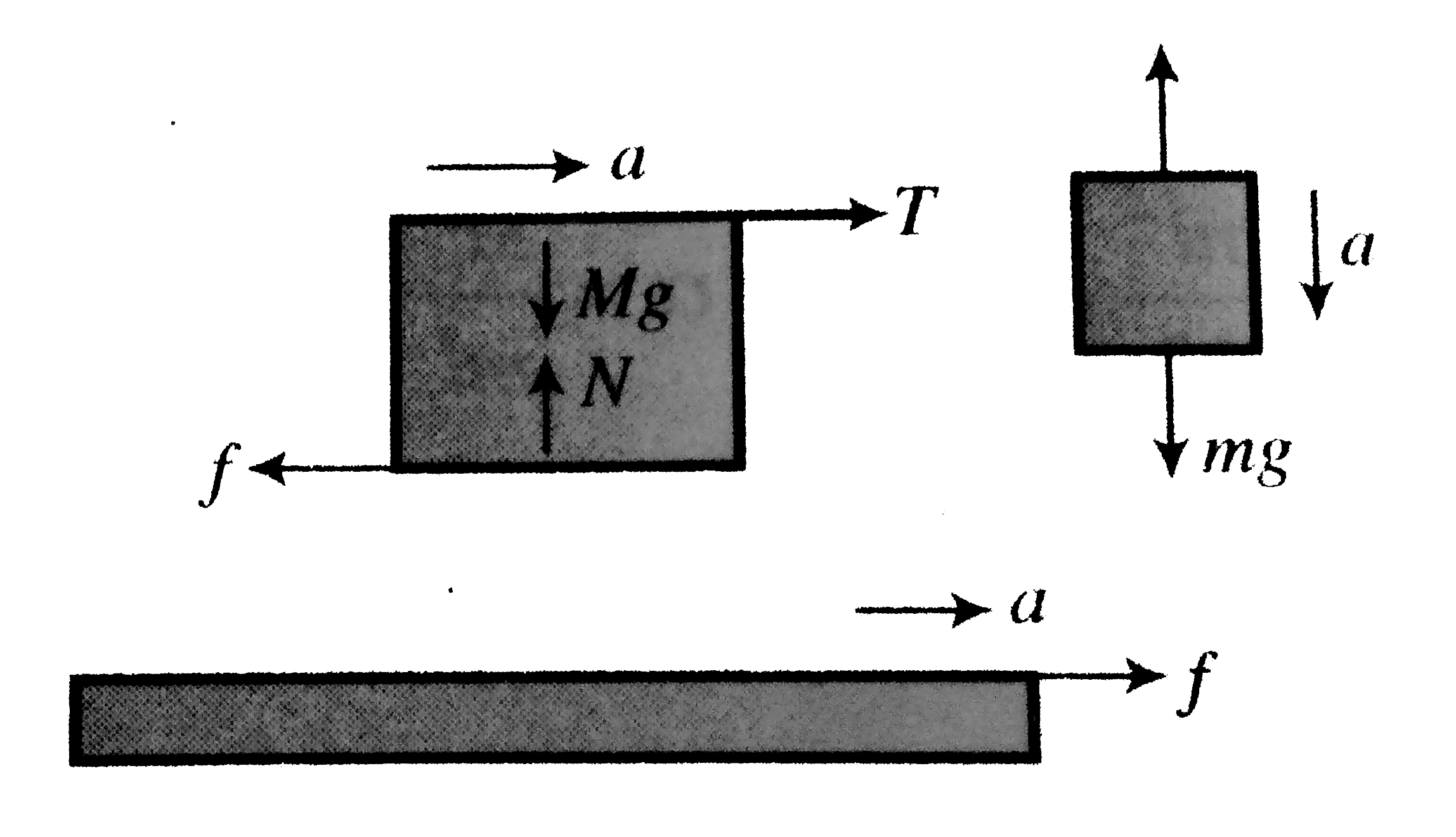 a. Since we are taking the limiting case.
a. Since we are taking the limiting case.
Therefore f= maximum friction between the block and the plank.
f=μN=μMg=μ(4)g
f=4μg ............i
Now writing equan of motion for all three
Mg−Tma(m=1kg) ........ii
or g−T=a
T−f=Ma(M=4kg)
or T−4μg=4a...........iii
or f=Ma or f=4a or 4μg=4a
or a=μg
Solving eqn ii, iii and iv for μ we get μ=19
Therefore minnimum value of μ should be 19 or μ≥19
b. At the time or toplling, normal reaction N will pass through the front edge as shown below:
So, torque of T about P≤torque of Mg about P
or Th≤(Mg)(b2) or T≤(Mg2)(bh)
From eqn ii, iii and iv we can find that
T=89g

Therefore 89g≤(Mg2)(bh)
or bh≥169M(M=4kg)
or (bh)≥49
Therefore minimum value of bh so that the block does not topple is 49
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Single Correct97videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Exercise 2.411videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
A small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
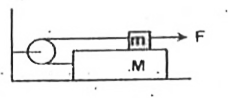
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?View SolutionA small block of mass m is placed on a plank of masss M .The block is connected to plank with the help of a light string passing over a light smooth pulley shown in fig. The co-efficient of static friction between the plank is μ The co-efficient of friction between the plank and the maximum horizontal force F applied on the block of mass m can make block not to slide relatively?
 View Solution
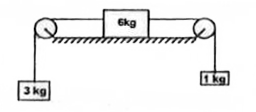
View SolutionThree blocks of masses 3 kg, 6 kg and 1 kg are connected by a string passing over two smooth pulleys attached at the two ends of the horizontal surface. If the co-efficient of friction between the block and the surface is 0.6, the frictional force acting on the block of mass 6 kg is
 View Solution
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
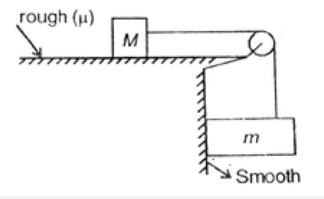
The minimum value of coefficient of friction μ such that system remains at rest , isView SolutionA body of mass 20kg is moving on a rough horizontal plane. A block of mass 3kg is connected to the 20 kg mass by a string of negligible mass through a smooth pulley as shown in the figure. The tension in the string is 27 N. The coefficient of kinetic friction between the heavier mass and the surface is (g = 10m/s2)
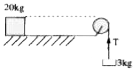 View Solution
View Solutionfind the acceleration of the block of mass M in the situation shown in figure. All the surfaces are frictionless and the pulleys and the string are light.
 View Solution
View SolutionA mass M is hung with a light inextensible string as shown in Find the tension in the horizontal part of the string .
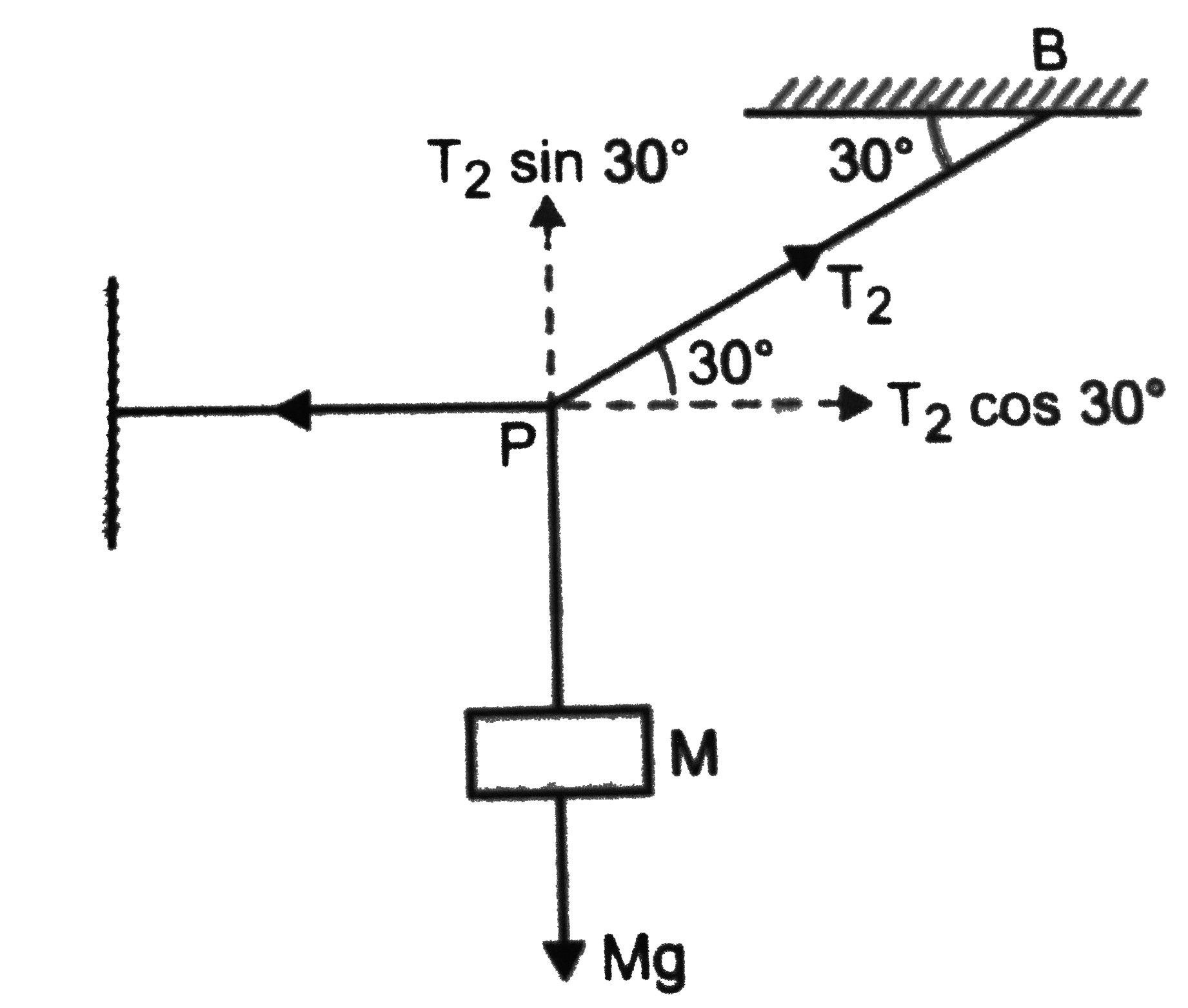 View Solution
View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m

If the coefficient of friction of friction μ is less than the above value, then downward acceleration of block m isView SolutionA block of mass M is hanging over a smooth and light pulley through a light string. The other end of the string is pulled by a constant force F. The kinetic energy of the block increases by 20J in 1s.
View SolutionA block of mass m1 = 4kg lying on a plane inclined at an angle of 30∘, is connected to another freely suspended block of mass m2 = 6kg with the help of a string passing over a smooth pulley as shown in the figure. The acceleration of each block is (g = 10 m/s2)
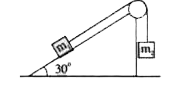 View Solution
View Solution

