A cylindrical object of outer diameter 20 cm and mass 2 kg flots in wter with its axis vertical. If it si lightly depressed and then released, find the time peiod of the resulting simple harmonic motion of the object.
To find the time period of the simple harmonic motion of a cylindrical object floating in water, we can follow these steps:
Step 1: Identify the parameters
- Outer diameter of the cylindrical object = 20 cm
- Mass of the object (m) = 2 kg
- Density of water (ρ) = 103kg/m3
- Acceleration due to gravity (g) = 10m/s2
Step 2: Calculate the radius of the cylinder
The radius (r) can be calculated from the diameter:
r=Diameter2=20cm2=10cm=0.1m
Step 3: Determine the volume of the submerged part
When the cylindrical object is slightly depressed, the volume (V) of the submerged part is given by:
V=πr2x
where x is the displacement from the equilibrium position.
Step 4: Calculate the buoyant force
The buoyant force (F_b) acting on the object when it is submerged is given by:
Fb=ρ⋅V⋅g=ρ⋅(πr2x)⋅g
Substituting the values:
Fb=103⋅(π(0.1)2)⋅10
Fb=103⋅π⋅0.01⋅10=103⋅π⋅0.1
Fb=100πN
Step 5: Set up the equation of motion
The restoring force (F) when the object is displaced is equal to the buoyant force:
F=m⋅a
Where a is the acceleration. Thus, we can write:
100π=2⋅a
a=100π2=50πm/s2
Step 6: Find the time period
The formula for the time period (T) of simple harmonic motion is given by:
T=2π√xa
In this case, the effective displacement is the volume displaced divided by the mass:
T=2π√mρ⋅πr2⋅g
Substituting the known values:
T=2π√2103⋅π⋅(0.1)2⋅10
T=2π√2103⋅π⋅0.01⋅10=2π√2100π=2π√150π
T=2π⋅1√50π=2π√50π
Step 7: Calculate the numerical value
Calculating the numerical value:
T≈0.5s
Thus, the time period of the resulting simple harmonic motion of the object is approximately 0.5 seconds.
---
- Outer diameter of the cylindrical object = 20 cm
- Mass of the object (m) = 2 kg
- Density of water (ρ) = 103kg/m3
- Acceleration due to gravity (g) = 10m/s2
The radius (r) can be calculated from the diameter:
r=Diameter2=20cm2=10cm=0.1m
When the cylindrical object is slightly depressed, the volume (V) of the submerged part is given by:
V=πr2x
where x is the displacement from the equilibrium position.
The buoyant force (F_b) acting on the object when it is submerged is given by:
Fb=ρ⋅V⋅g=ρ⋅(πr2x)⋅g
Substituting the values:
Fb=103⋅(π(0.1)2)⋅10
Fb=103⋅π⋅0.01⋅10=103⋅π⋅0.1
Fb=100πN
The restoring force (F) when the object is displaced is equal to the buoyant force:
F=m⋅a
Where a is the acceleration. Thus, we can write:
100π=2⋅a
a=100π2=50πm/s2
The formula for the time period (T) of simple harmonic motion is given by:
T=2π√xa
In this case, the effective displacement is the volume displaced divided by the mass:
T=2π√mρ⋅πr2⋅g
Substituting the known values:
T=2π√2103⋅π⋅(0.1)2⋅10
T=2π√2103⋅π⋅0.01⋅10=2π√2100π=2π√150π
T=2π⋅1√50π=2π√50π
Calculating the numerical value:
T≈0.5s
Topper's Solved these Questions
Similar Questions
A cylindrical block of wood of mass M is floating n water with its axis vertica. It is depressed a little and then released. Show that the motion of the block is simple harmonic and find its frequency.
View SolutionA cylindrical object of outer diameter 20 cm height 20 cm and density 8000 kgm−3 is supported by a vertical spring and is half dipped in water as shown in figue. a. Figure the elongation of the spring in equilibrium condition. b. If the object is sllightlly depressed and relation, find the time period of resulting oscillations of the objcet. The spring constant =500Nm−1.

View Solution
Knowledge Check
A cylindrical of wood (density =600kgm−3) of base area 30cm2 and height 54cm, floats in a liquid of density 900kg−3 The block is deapressed slightly and then released. The time period of the resulting oscillations of the block would be equal to that of a simple pendulum of length (nearly) :
A26cmB52cmC36cmD65cmA copper rod (length =2.0m, radius =3.0×10−3m) hangs down from the ceiling. A 9.0kg object is attached to the lower end of the rod. The rod acts as a ''spring'' and the object oscillates vertically with a small amplitude. Ignoring the rod's mass, find the frequency f of the simple harmonic motion.
A66HzB13HzC93HzD37HzA particle of mass 0.2 kg moves with simple harmonic motion of amplitude 2 cm. If th~ total energy of the particle is 4×10−5 J, then the time period of the motion is
A2π secondsB3π2 secondsCπ secondsDπ2 seconds
A cylindrical plastic bottle of negligible mass is filled with 310 ml of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic montion angular frequency ω. If the radius of the bottle is 2.5 cm then ω is close to: (density of water =103kg/m3)
View SolutionA vertical U-tube of uniform cross-section contains water upto a height of 30 cm. show that if the water in one limb is depressed and then released, its up and down motion in the two limbs of the tube is simple harmonic and calculate its time-period.
View SolutionA mass m is dropped in a tunnel along the diameter of earth from a height h(<<R) above the surface of earth. Find the time period of motion. Is the motion simple harmonic?
View Solution15.A small circular loop of conducting wire has radius a and carries current I. It is placed in a uniform magnetic field B perpendicular to its plane such that when rotated slightly about its diameter and released it starts performing simple harmonic motion of time period T.If the mass of the loop is m then:
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
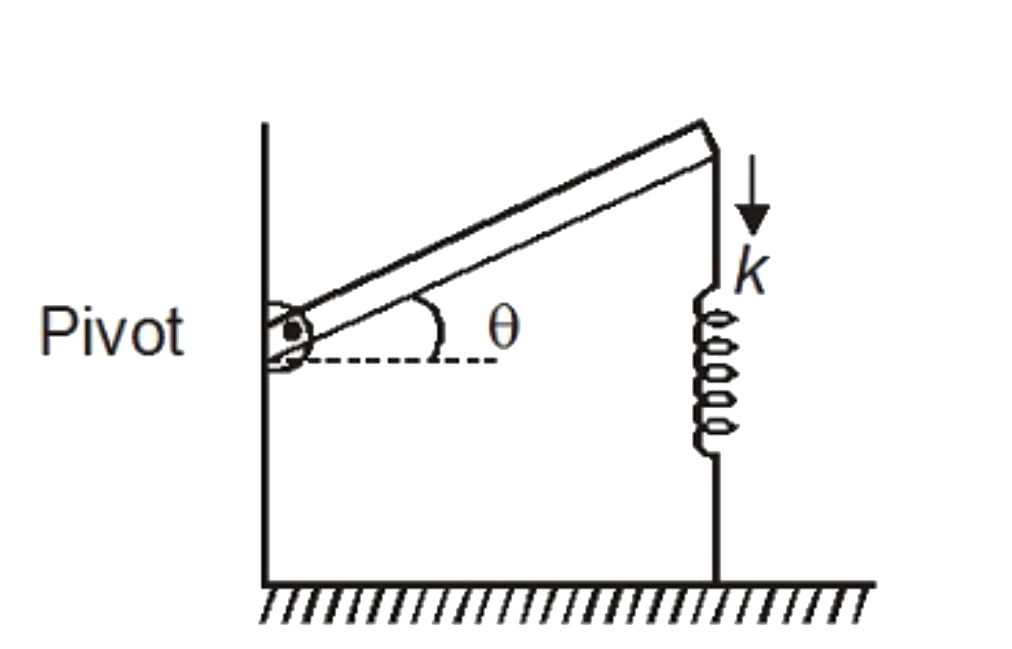
View Solution
