A cylindrical piece of cork of density ρ, base area A and height h, floats in a liquid of density ρ1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically, with a period T=2π√hρρ1g, where 'ρ' is the density of the cork. Solution in Kannada
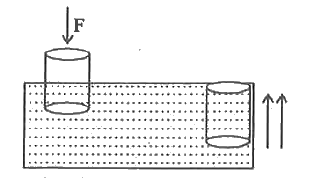
Restoring force =− weight of liquid displaced =−(ρ1Ay)g
Applied force F=ma
i.e. F=(ρAh)a
Hence, ρAha=−ρAyg
or ya=∣∣∣−ρhρ1g∣∣∣
We know that period of oscillation,
T=2π√displacementaccelertion ∴T=2π√ρρ1g
If .ρ. of the floating body is equal to the density of liquid then,
T=2π√hg.
Topper's Solved these Questions
- BOOK - SUBHASH PUBLICATIONCHAPTER - OSCILLATIONSEXERCISE - FIVE MARKS QUESTIONS WITH ANSWERS4videos
OSCILLATIONS
- BOOK - SUBHASH PUBLICATIONCHAPTER - MOTION IN PLANEEXERCISE - NUMERICALS WITH SOLUTIONS47videos
MOTION IN PLANE
- BOOK - SUBHASH PUBLICATIONCHAPTER - PHYSICAL WORLDEXERCISE - TWO MARKS QUESTIONS WITH ANSWERS30videos
PHYSICAL WORLD
Similar Questions
Arrive an expression for time period of simple pendulum.
06:44View SolutionTwo forces 8N and 5N are acting at a point on a body at an angle 120∘ then find the (i) magnitude and (ii) direction of their resultant.
02:16View SolutionMathematics is the language of physics. Justify the statement.
07:27View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hrho)/(rho_(1)g))
07:24View SolutionA cylidrical wooden piece of cork floats in a liquid of density σ. The cork is depressed slightly and released. Show that the cork will oscillate up and down simple harmonicaly with a period.
T=2π√ρhσg, where ρ is the density of the cork.09:47View Solutionआधार क्षेत्रफल A तथा ऊँचाई h के एक कॉर्क का बेलनकार दुकड़ा pt घनत्व के किसी द्रव में तैर रहा है | कॉर्क को थोड़ा निचे दबाकर स्वतंत्र छोड़ देते है, यह दर्शाइए कि कॉर्क ऊपर-निचे सरल आवर्त दोलन करता है जिसका आवर्तकाल
T=2π√hpp1g है |
यहाँ p कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए ) |03:57View Solutionआधार क्षेत्रफल A तथा ऊंचाई के h एक कॉर्क का बेलनाकार टुकड़ा pl घनत्व के किसी द्रव में तैर रहा है । कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते है , यह दर्शाइये कि कॉर्क ऊपर - नीचे सरल आवर्त दोलन करता है जिसका आवर्तकाल T=2π√hpplg है ।
यहाँ ρ कॉर्क का घनत्व है ( द्रव कि श्यानता के कारण अवमन्दन को नगण्य मानिए ।)02:55View Solutionआधार क्षेत्रफलA तथा ऊँचाई h के कॉर्क का बेलनाकार टुकड़ा ρ1 घनत्व के किसी द्रव पर तैर रहा है। कॉर्क को थोड़ा नीचे दबाकर स्वतंत्र छोड़ देते है , यह दर्शाइए की कॉर्क ऊपर - नीचे सरल आवर्त दोलन करता है जिसका आवर्त T=2v√hρρ1g है।
यहाँ ρ कॉर्क का घनत्व है (द्रव की श्यानता के कारण अवमंदन को नगण्य मानिए)07:28View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p1. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).02:55View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).View SolutionA cylindrical piece of cork of base area A and height h floats in a liquid of density rho_(1) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hrho)/(rho_(1)g))
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).08:27View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density ρ1. The cork is depressed slightly and then released. The cork oscillates up and down simple harmonically with period is (ρ is the density of cork)
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density p_(l) . The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period T=2pisqrt((hp)/(p_(1)g)) where p is the density of cork. (Ignore damping due to viscosity of the liquid).
View SolutionA cylindrical piece of cork of density of base area A and height h floats in a liquid of density pl. The cork is depressed slightly and then released. Show that the cork oscillates up and down simple harmonically with a period
T=2π√hpp1g
where p is the density of cork. (Ignore damping due to viscosity of the liquid).View Solution

