A cylindrical vessel contains a liquid of density $ρ$ up to height $h$ . The liquid is closed by a piston of mass $m$ and area of cross section $A$ . There is a small hole at the bottom of the vessel. The speed $v$ with which the liquid comes out of the hole is

A

$\sqrt{2 g h}$

B

$\sqrt{2 (g h + \frac{m g}{ρ A})}$

C

$\sqrt{2 (g h + \frac{m g}{A})}$

D

$\sqrt{2 (g h + \frac{m g}{A})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Applying Bernoulli's theorem at point $1$ and $2$ difference in pressure energy between $1$ and $2 =$ difference in kinetic energy between $1$ and $2$ .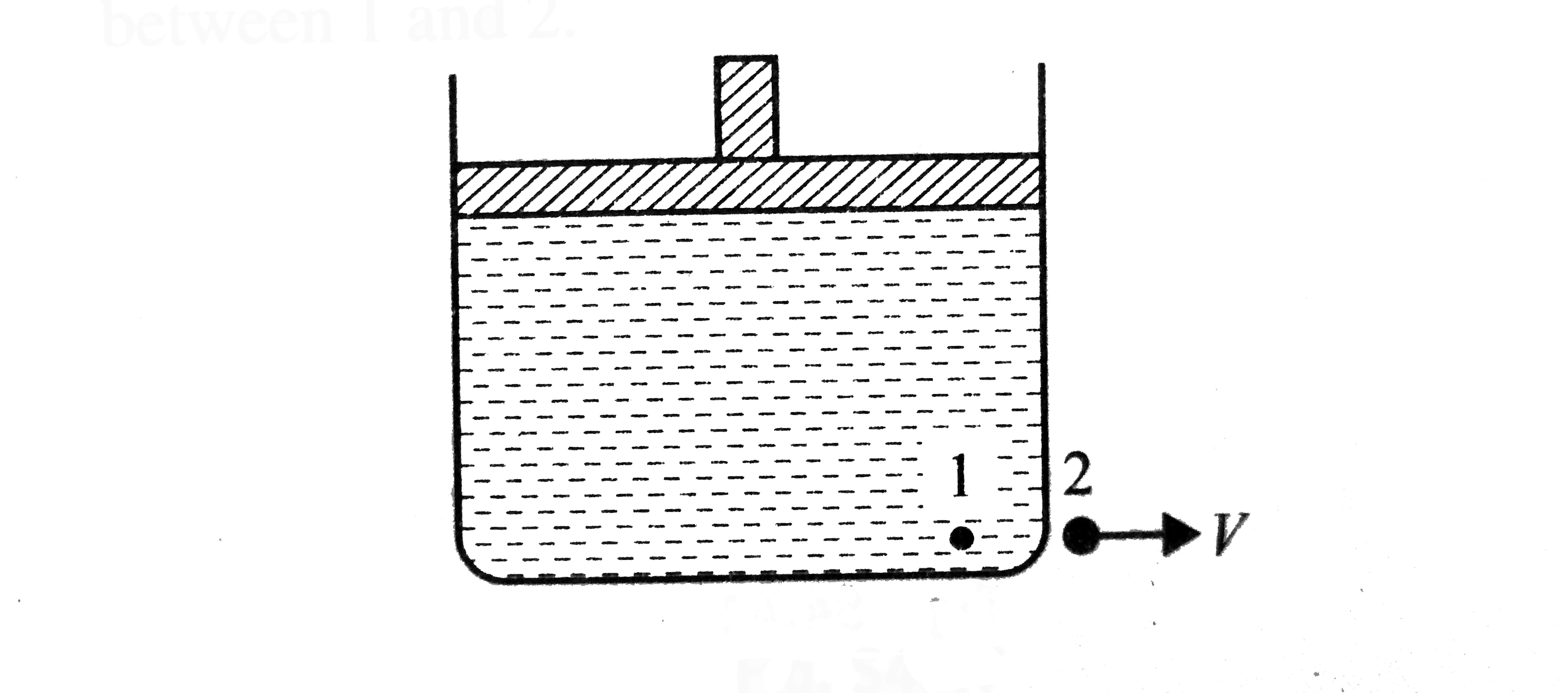
Here $ρ h g = \frac{m g}{A} = \frac{1}{2} ρ v^{2}$
or $v = \sqrt{(2 g \frac{h_{2 m g}}{ρ A}) = \sqrt{2 (g h + \frac{m g}{ρ A})}}$

|

Class 11 PHYSICS FLUID MECHANICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A cylindrical vessel contains a liquid of density $ρ$ up to height $h$ . The liquid is closed by a piston of mass $m$ and area of cross section $A$ . There is a small hole at the bottom of the vessel. The speed $v$ with which the liquid comes out of the hole is

A $\sqrt{2 g h}$
B $\sqrt{2 (g h + \frac{m g}{p A})}$
C $\sqrt{2 (g h + \frac{m g}{A})}$
D $\sqrt{2 g h + \frac{m g}{A}}$
In a cylindrical vessel containing liquid of density $ρ$ , there are two holes in the side walls at heights of $h_{1}$ and $h_{2}$ respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole, for which the range of efflux would be maximum, will be –

A $h_{2} - H_{1}$
B $H_{2} + H_{2}$
C $\cdot h_{2} - h_{2} \frac{)}{2}$
D $\frac{h_{2} + h_{1}}{2}$
In a cylindrical vessel containing liquid of density $ρ$ there are two holes in the side walls at heights of $h_{1}$ and $h_{2}$ respectively such that the range of efflux at the bottom of the vessel is same. The height of a hole for which the range of efflux would be maximum, will be

A $h_{2} - h_{1}$
B $h_{2} + h_{1}$
C $\frac{h_{2} - h_{1}}{2}$
D $\frac{h_{2} + h_{1}}{2}$

CENGAGE PHYSICS-FLUID MECHANICS-Single Correct

Home
Ask Doubt
Profile