A cylindrical vessel is filled with water upto a height of 1m. The cross-sectional area of the orifice at the bottom is (1/400) that of the vessel.
(a) What is the tiome required to empty the tank through the orifice at the bottom?
(b) What is the time required for the same amount of water to flow out if the water level in tank is maintained always at a height of 1m from orifice?
The correct Answer is:A, B, C
(a) Time taken to empty the tank (has been derived in theory) is
t=2Aa√2g√H
Given, Aa=400
Substituting the value we have,
t=2×400√2×9.8√1
=180s=3min
(b) Rate of flow of water Q=a√2gH=constant
Total volume of water V=AH
∴ Time take to empty the tank with constant rate
t=VQ=AHa√2gH
400×1√2×9.8×1
=90s=1.5min
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.1
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Example 13.2
1 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Level 2 Comprehension Based
7 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionWater flows out of a small hole in the wall of a large tank near its bottom. What is the speed of efflux of water when height of water level in the tank is 5.0 m ?
View Solution
Knowledge Check
Water is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
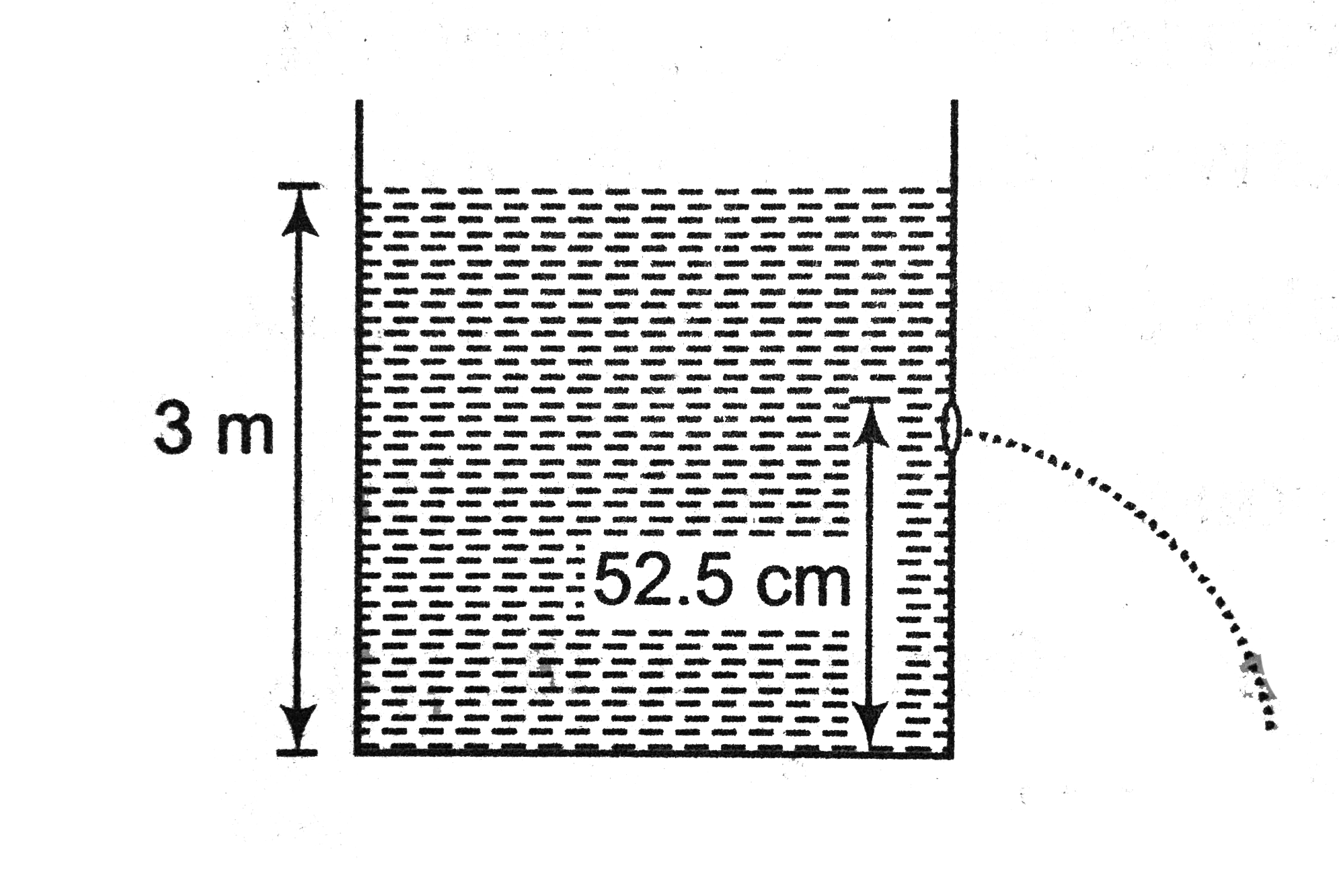 A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2
A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2What is filled in a cylindrical container to a height of 3m. The ratio of the cross-sectional area of the orifice and the beaker is 0.1. The square of the speed of the liquid coming out from the orifice is (g=10m/s2).
A50m2/s2B50.5m2/s2C51m2/s2D52m2/s2The velocity of flow of a liquid through an orifice at the bottom of a tank depends on the :
Aarea of the cross - section of the orificeBheight of the liquid above the orificeCacceleration due to gravityDboth (b) and (c )
A cylindrical vessel of hieght h and base area S is filled with water. An orifice of area s<<S is made at the bottom of the vessel. Neglection viscosity find how soon the vessel would be emptied.
View SolutionA cylindrical tank with a large diameter is filled with water to a depth D =0.30 m. A hole of cross-sectional area A = 6.2 cm2 in the bottom of the tank allows water to drain out. (a) What is the drainage rate in cubic meters per second? (b) At what distance below the bottom of the tank is the cross-sectional area of the stream equal to one half the area of the hole?
View SolutionIn a container, filled with water upto a height h, a hole is made in the bottom. The velocity of water flowing out of the hole is
View SolutionA cylindrical vessel of cross section A contains water to a height h. There is a hole in the bottom of radius 'a'. The time in which it will be emptied is:
View SolutionThe velocity of efflux of a liquid through an orifice in the bottom of a tank does not depend upon
View Solution
