(a) define electrie flux. Write its, S.I unit.
" Gauses's law in electrostatis is true for any closed surface, no matter what its shape or size is.
Justify this statement with the help of a suitable example.
(b) Use Gauss's law to prove that the electric field inside a uniformly charged spherical shell is zero.
Step-by-Step Solution
1. Definition of Electric Flux:
Electric flux (Φ) is defined as the total number of electric field lines passing through a given surface area. It can be mathematically expressed as:
Φ=∫E⋅dA
where E is the electric field vector and dA is the differential area vector.
2. SI Unit of Electric Flux:
The SI unit of electric flux can be derived from the formula. The electric field E has units of Newtons per Coulomb (N/C), and the area A has units of square meters (m²). Therefore, the unit of electric flux is:
SI Unit of Electric Flux=N m2/CorNm2/C
3. Justification of Gauss's Law:
Gauss's law states that the electric flux through any closed surface is proportional to the charge enclosed within that surface. This law holds true regardless of the shape or size of the closed surface.
Example:
Consider two different closed surfaces: a cube and a sphere, both enclosing the same charge Q. According to Gauss's law:
Φ=Qϵ0
Here, ϵ0 is the permittivity of free space. Since both surfaces enclose the same charge, the electric flux through both surfaces will be the same, demonstrating that Gauss's law is independent of the shape of the surface.
---
(b) Proving Electric Field Inside a Uniformly Charged Spherical Shell is Zero
1. Understanding the Setup:
Consider a uniformly charged spherical shell with total charge Q. The charge resides on the surface of the shell and does not penetrate the interior.
2. Applying Gauss's Law:
To find the electric field inside the shell, we will use Gauss's law:
Φ=Qencϵ0
where Qenc is the charge enclosed by a Gaussian surface.
3. Choosing a Gaussian Surface:
Select a spherical Gaussian surface of radius r such that r is less than the radius of the spherical shell. Since there is no charge enclosed within this Gaussian surface (the charge is only on the shell), we have:
Qenc=0
4. Calculating the Electric Flux:
Substituting Qenc=0 into Gauss's law gives:
Φ=0ϵ0=0
5. Relating Flux to Electric Field:
The electric flux through the Gaussian surface can also be expressed as:
Φ=E⋅A
where A is the surface area of the Gaussian sphere. Since the flux is zero, we have:
E⋅A=0
Since the area A is not zero, it follows that:
E=0
6. Conclusion:
Thus, we conclude that the electric field inside a uniformly charged spherical shell is zero:
E=0(inside the shell)
---
Electric flux (Φ) is defined as the total number of electric field lines passing through a given surface area. It can be mathematically expressed as:
Φ=∫E⋅dA
where E is the electric field vector and dA is the differential area vector.
The SI unit of electric flux can be derived from the formula. The electric field E has units of Newtons per Coulomb (N/C), and the area A has units of square meters (m²). Therefore, the unit of electric flux is:
SI Unit of Electric Flux=N m2/CorNm2/C
Gauss's law states that the electric flux through any closed surface is proportional to the charge enclosed within that surface. This law holds true regardless of the shape or size of the closed surface.
Consider two different closed surfaces: a cube and a sphere, both enclosing the same charge Q. According to Gauss's law:
Φ=Qϵ0
Here, ϵ0 is the permittivity of free space. Since both surfaces enclose the same charge, the electric flux through both surfaces will be the same, demonstrating that Gauss's law is independent of the shape of the surface.
Consider a uniformly charged spherical shell with total charge Q. The charge resides on the surface of the shell and does not penetrate the interior.
To find the electric field inside the shell, we will use Gauss's law:
Φ=Qencϵ0
where Qenc is the charge enclosed by a Gaussian surface.
Select a spherical Gaussian surface of radius r such that r is less than the radius of the spherical shell. Since there is no charge enclosed within this Gaussian surface (the charge is only on the shell), we have:
Qenc=0
Substituting Qenc=0 into Gauss's law gives:
Φ=0ϵ0=0
The electric flux through the Gaussian surface can also be expressed as:
Φ=E⋅A
where A is the surface area of the Gaussian sphere. Since the flux is zero, we have:
E⋅A=0
Since the area A is not zero, it follows that:
E=0
Thus, we conclude that the electric field inside a uniformly charged spherical shell is zero:
E=0(inside the shell)
Similar Questions
Define electric flux. Write its SI unit. A charge q is enclosed by a spherical surface of radius R. If the radius is reduced to half, how would the electric flux through the surface change ?
View Solution(a) Define electric flux. Write its S.I. units.
(b) Using Gauss's law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
(c ) How is the field directed if (i) the sheet is positively charged, (ii) negatively charged ?View Solution
Knowledge Check
- Question 1 - Select One
Assertion : Total flux through a closed surface is zero if no charge is enclosed by the surface.
Reason : Gauss law is true for any closed surface, no matter what its shape or size is.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf both assertion and reason are false.
(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
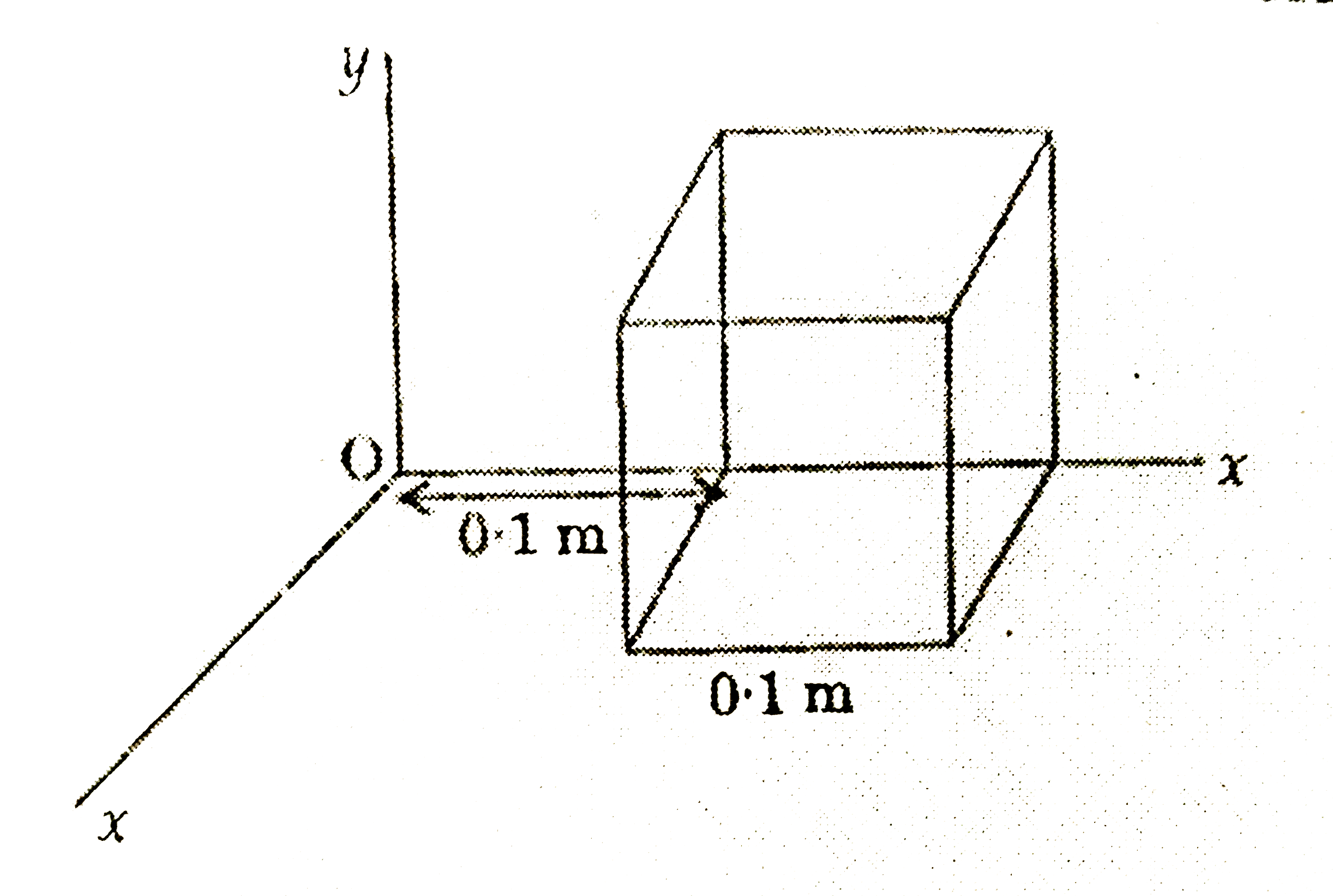
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.View Solution(a) Define electric flux. Write its SI units.
(b) The electric field components due to a charge inside the cube of side 0.1 m are as shown :
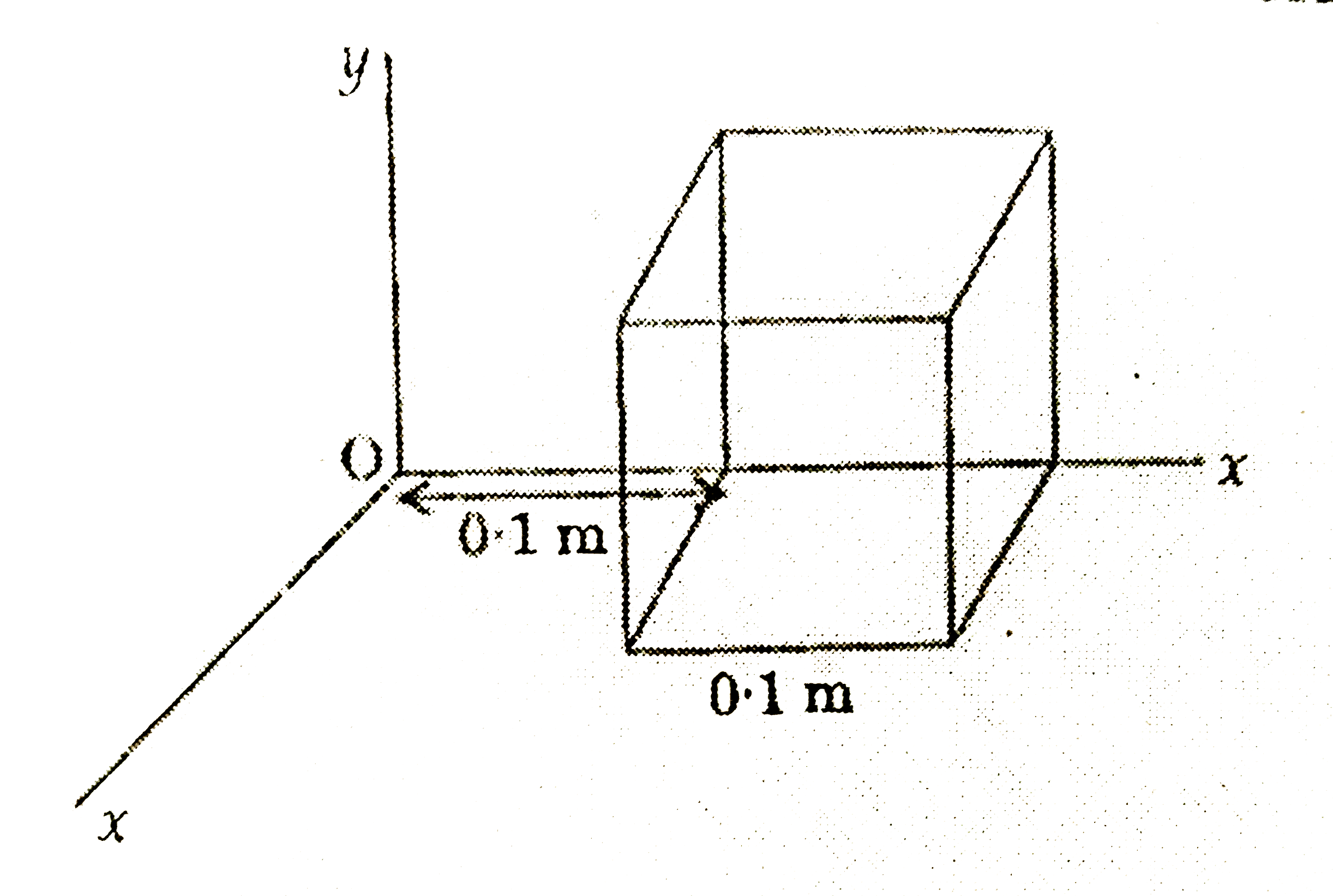
Ex=αx, where α=500N/C−m
Ey=0,Ez=0.
Calculate (i) the flux through the cube, and (ii) the charge inside the cube.View SolutionDefine the term .electric flux.. Write its SI units. What is the flux due to electric field →E=3×103ˆiN/C through a square of side 10 cm, when it is held normal to →E ?
View SolutionA spherical shell made of plastic, contains a charge Q distributed uniformly over its surface. What is the electric field inside the shell? If the shell is hammered to deshape it without altering the charge. Will the field inside be changed? What happend if the shell is made of a metal?
View SolutionA spherical conducting shell of inner radius r1 and outer radius r2 has a charge Q.
(a) A charge q is placed at the center of the shell. What is the surface charge density on the inner and outer surfaces of the shell ?
(b) Is the electric field intensity inside a cavity (with no charge) zero, even if the shell is not spherical, but has any irregular shape ? Explain.View SolutionConsider a point charge q=1mC placed at a corner of a cube of sides 10 cm . Determine the electric flux through each face of the cube.
Strategy : We will learn about the utility of symmetry in solving problems with the help of Gauss's law . Here we'll use the symmetry of the situation,which involves the faces joining at the corner at which the charge resides.

(a) A charge q is placed atthe corner of a cube. (b) By surrounding the charge with a series of cubes such that the charge is at the centre of a larger cube, we have created an arrangement sufficiently symmetric to be able to solve for desired flux values.
You can see from figure that for these faces →E.ˆn=0. Since the normal is perpendicular to the surfaces while the electric field goes off in a spherically symmetric pattern and lies in the sides . In other words , the electric field that originates at the charge is tangential to the surface of these three sides. This means there is no flux through these sides. The electric flux through each of the remaining three faces of the be must be equal by symmetry . We'll referto these faces with the label F.
To fidn the flux through each of the sides F, we acan use a technique that puts the single charge in the middle of a larger cube. It takes seven other similarly placed cubes to surrounds the points charge q completely in figre. The charge is at the dead centre of the enw larger cube. So, the flux through each of the six sides of the large cube will now have an electric flux of one sixth of the total flux F. So given that the total structure is completely symmetric, the flux through a side F is one fourth of the flux through the larger side.View SolutionA small metal sphere carrying charge +Q is located at the centre of a spherical cavity inside a large uncharged metallic spherical shell as shown in the figure. Use Gauss’s law to find the expressions for the electric field at points p1 and p2 . Also draw the pattern of electric field lines in this arrangement.
 View Solution
View Solution

