A disc is fnst spinned and then placed gentlyon a rough floor with its surface horizontal. Will centre of mass of disc advance in some direction ? Explain.
Step by step video & image solution for A disc is fnst spinned and then placed gentlyon a rough floor with its surface horizontal. Will centre of mass of disc advance in some direction ? Explain. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Conceptual MCQs Single Option Correct
39 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Numerical MCQs Single Option Corrrect
39 Videos
- RIGID BODIES AND ROTATIONAL MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - RIGID BODIES AND ROTATIONAL MOTIONEXERCISE - Practice exercise
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - WORK, ENERGY AND POWEREXERCISE - unsolved
1 Videos
Similar Questions
A semicircle disc of mass M and radius R is held on a rough horizontal surface as shown in figure. The centre of mass C of the disc is at a distance of 4R3π from the point O. Now the disc is released from this position so that it starts rolling without slipping. Find
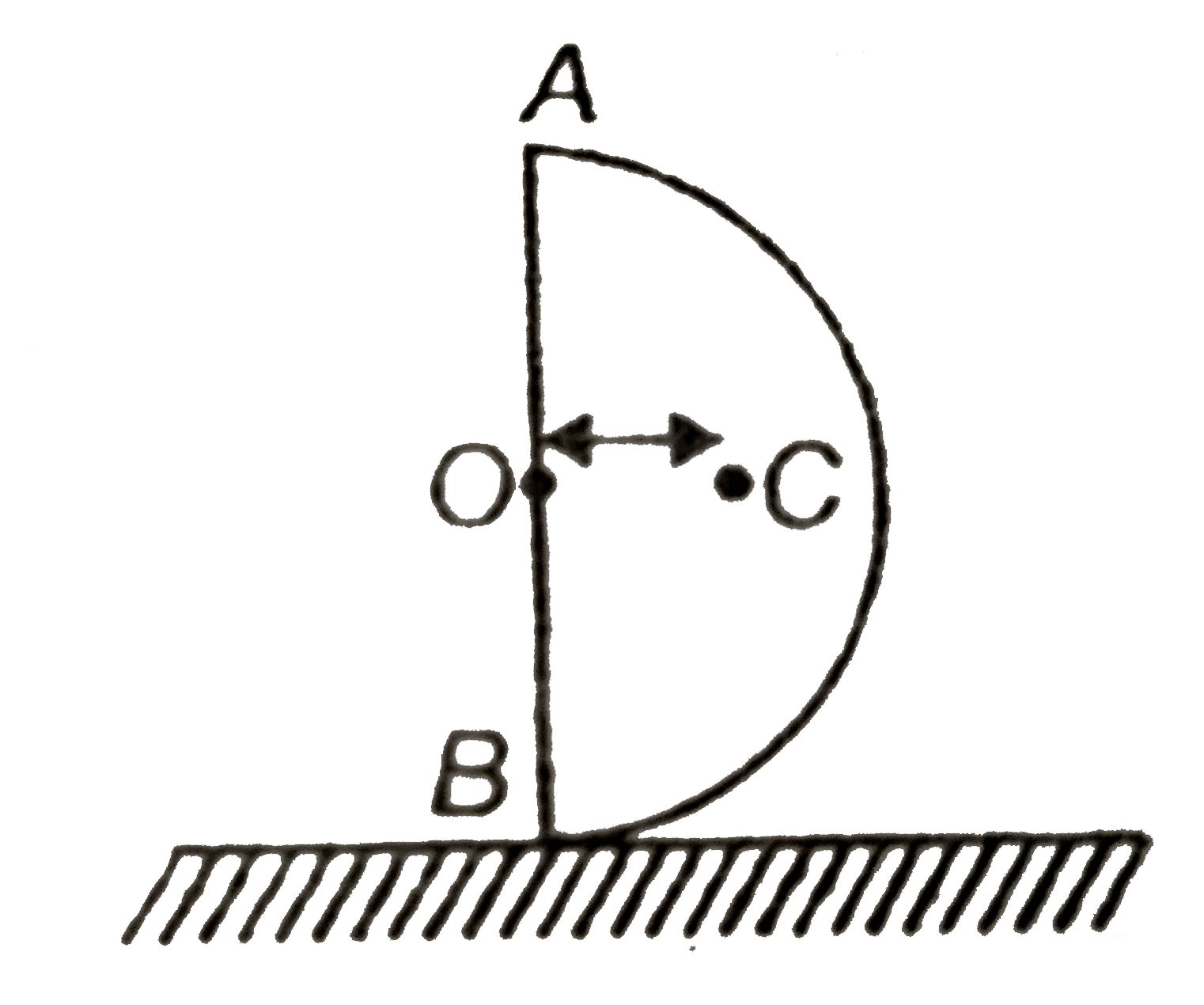
(a) The angular acceleration of the disc at the moment it is relased from the given position.
(b) The minimum co-efficient of fricition between the disc and ground so that it can roll without slipping.
View SolutionA disc of radius R and mass m is projected on to a horizontal floor with a backward spin such that its centre of mass speed is v0 and angular velocity is ω0. What must be the minimum value of ω0 so that the disc eventually returns back?
View Solution
Knowledge Check
A disc of mass m and radius r placed on a routh horizontal surface. A cue of mass m hits the disc at a height h from the axis passing through centre and parallel to the surface. The disc will start pure rolling for.
Ah<r3Bh=r2Ch>r2Dh≥r2A uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position ifAω0R=2V0Bω0R<2V0Cω0R>2V0DData insufficientA uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position ifAω0R>2V0Bω0R=2V0Cω0R<2V0DIt is impossible
A uniiform disc of radius r spins with angular velocity ω and angular acceleration α. If the centre of mass of the disc has linear acceleration a, find the magnitude and direction of aceeleration of the point 1,2, and 3.
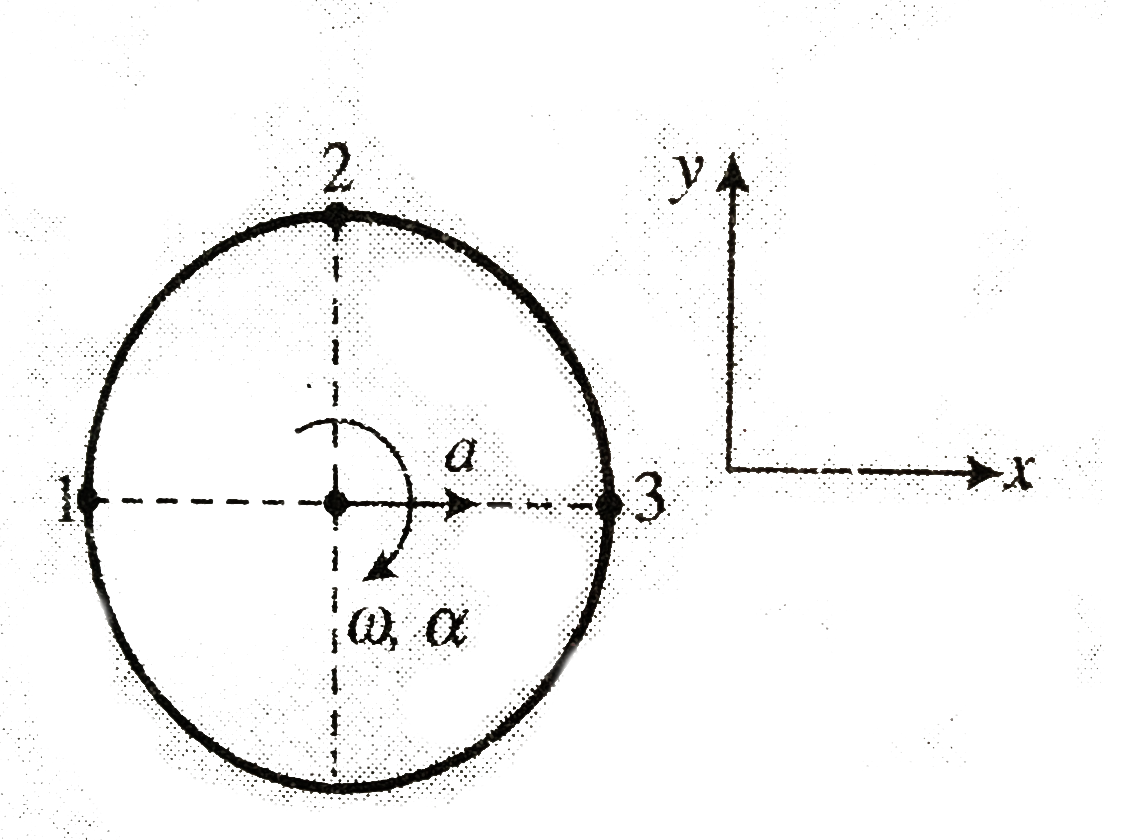
View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc

View SolutionA circular disc with a groove along its diameter is placed horizontally on a rough surface. A block of mass 1 kg is placed as shown. The co-efficient of friction between the block and all surfaces of groove and horizontal surface in contact is μ=25. The disc has an acceleration of 25m/s2 towards left. Find the acceleration of the block with respect to disc. Given cosθ=45, sinθ=35.
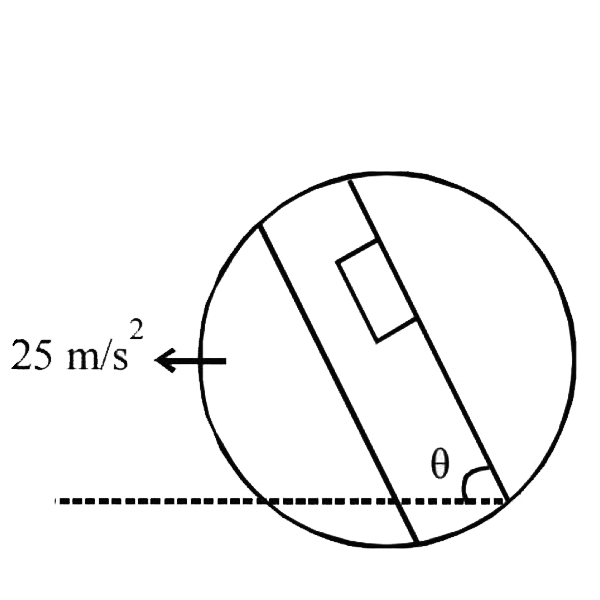
View SolutionA disc shaped body (having a hole shown in the figure) of mass m=10kg and radius R=109m is performing pure rolling motion on a rough horizontal surface. In the figure point O is geometrical center of the disc and at this instant the centre of mass C of the disc is at same horizontal level with O. The radius of gyration of the disc about an axis pasing through C and perpendicular to the plane of the disc is R2 and at the insant shown the angular velocity of the disc is ω=√gR rad/sec in clockwise sence. g is gravitation acceleration =10m/s2. Find angular acceleation α ( in rad/s2) of the disc at this instant.

View SolutionA uniform disc of radius R is spinned to the angular velocity ω and then carefully placed on a horizontal surface. How long will the disc be rotating on the surface if the friction coeffiecient is equal to k? The pressure exerted by the disc on the surface can be neglected as uniform.
View Solution
