Consider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc
Let us apply Newton's laws on disc in horizontal direction
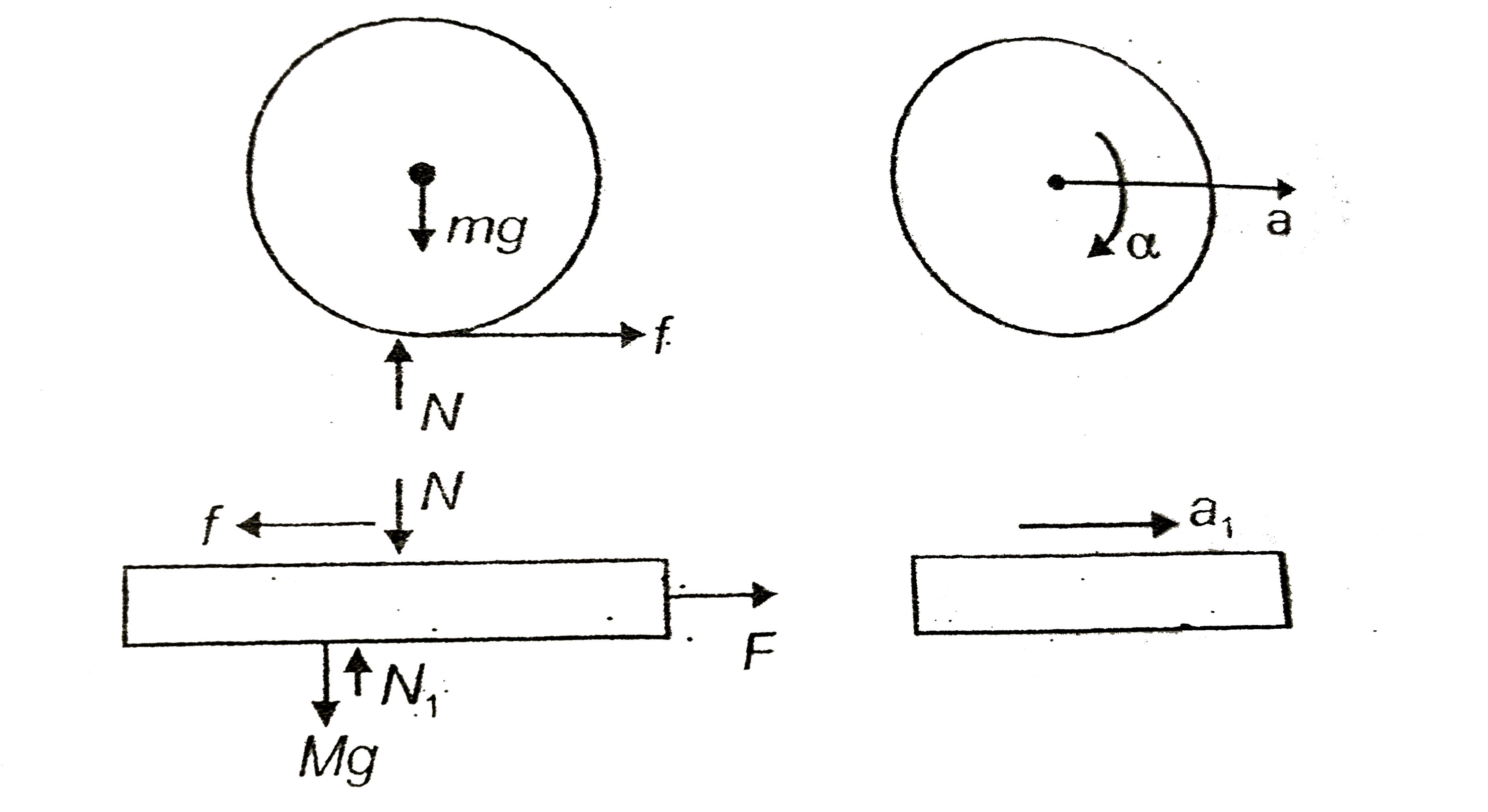
f=ma……..(i)
For plank
F−f=Ma1……….(ii)
Applying torque equation on disc about centre of mass
τ=lα
⇒fR=mR22α........(iii)
For pure rolling
a1=a+Rα.......(iv)
Solving the four equations, we get
f=Fmm+3M, α=2F(m+3M)R
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)62videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)57videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself63videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTECHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTECHAPTER - TEST 1EXERCISE - EXERCISE9videos
TEST 1
Similar Questions
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.
View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
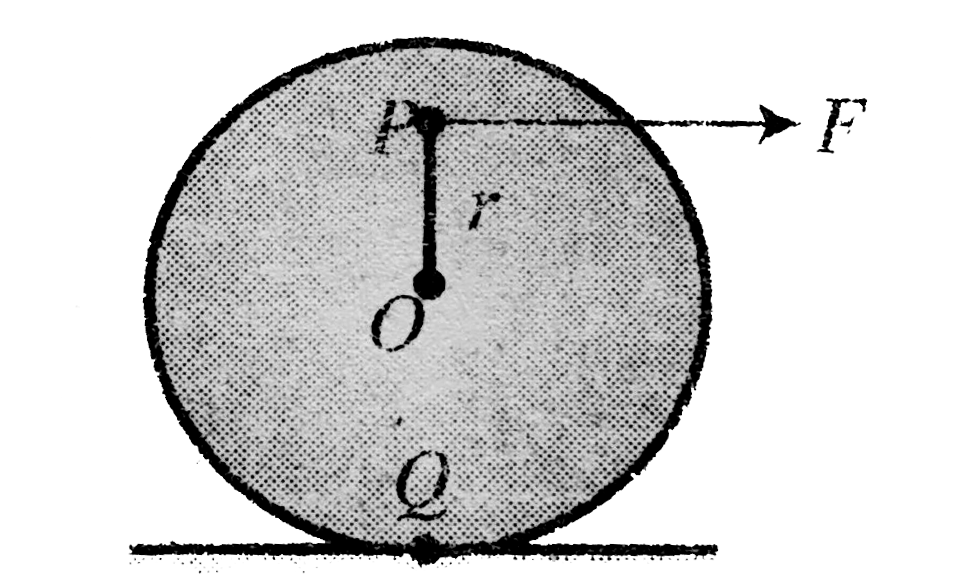
angular acceleration of the disc. (rads−1)View Solution
Knowledge Check
- Question 1 - Select One
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.
Acceleration of the plank isA3F16mB11F8mC9F4mDZero - Question 2 - Select One
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.
Force of friction between the disc and the plank isAF2BF4CF3D2F3 - Question 3 - Select One
A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.
Acceleration of the plank isAF2mB3F4mCF4mD3F2m
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.
Friction force acting between the sphere and the plank isView SolutionA plank with a uniform sphere placed on it rests on a smooth horizontal plane. The plank is pulled to the right by a constant force F. It the sphere does not slip over the plank, then
View SolutionA plank with a uniform sphere placed on it. Rests on a smooth horizontal plane. Plank is pulled to right by a constant force F. It the sphere does not slip over the plank.
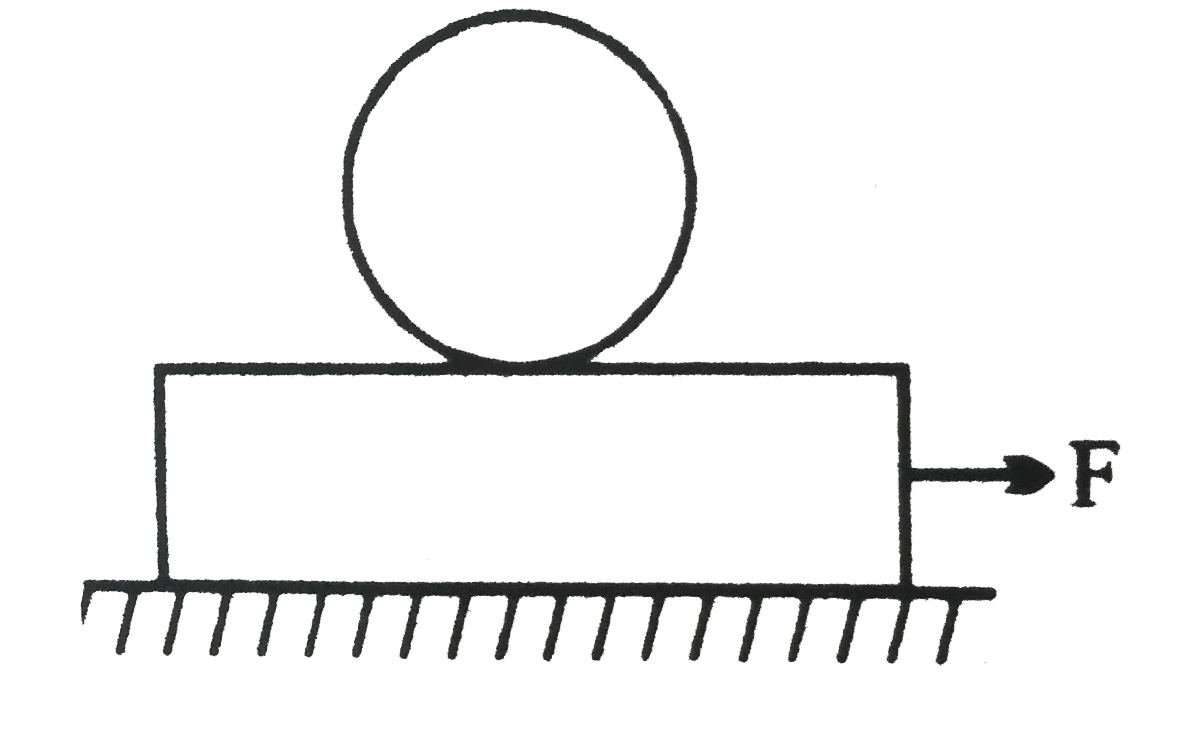. View SolutionA block of mass m is on the smooth horizontal surface of a plank of mass M The plank is on smooth horizontal surface Now, a constant horizontal force F acts on M. Now, for a person standing on the ground:
View SolutionA disc is pulled by a force F acting at a point above the centre of mass of the disc.
The direction of frictional force (fr) acting on disc pushed on a rough surface will be represented by.View Solution