A disc of mass 3 m and a dise of mass m are connected by a massless sping of stiffness k. The heavier is disc placed on the ground with the spring vertical and lighter disc on top from its equilibrium position the upper disc is pushed down by a distance δ and released. Then.
if δ>3mgk the lower desc will bounce up.
if δ=2mgk maximum normal reaction fron on lower disc = 6mg .
if δ=2mgk maximum normal reaction from ground on lower disc = 4 mg.
if δ>4mgk, the lower disc will bounce up
The correct Answer is:B, D
At equilirium
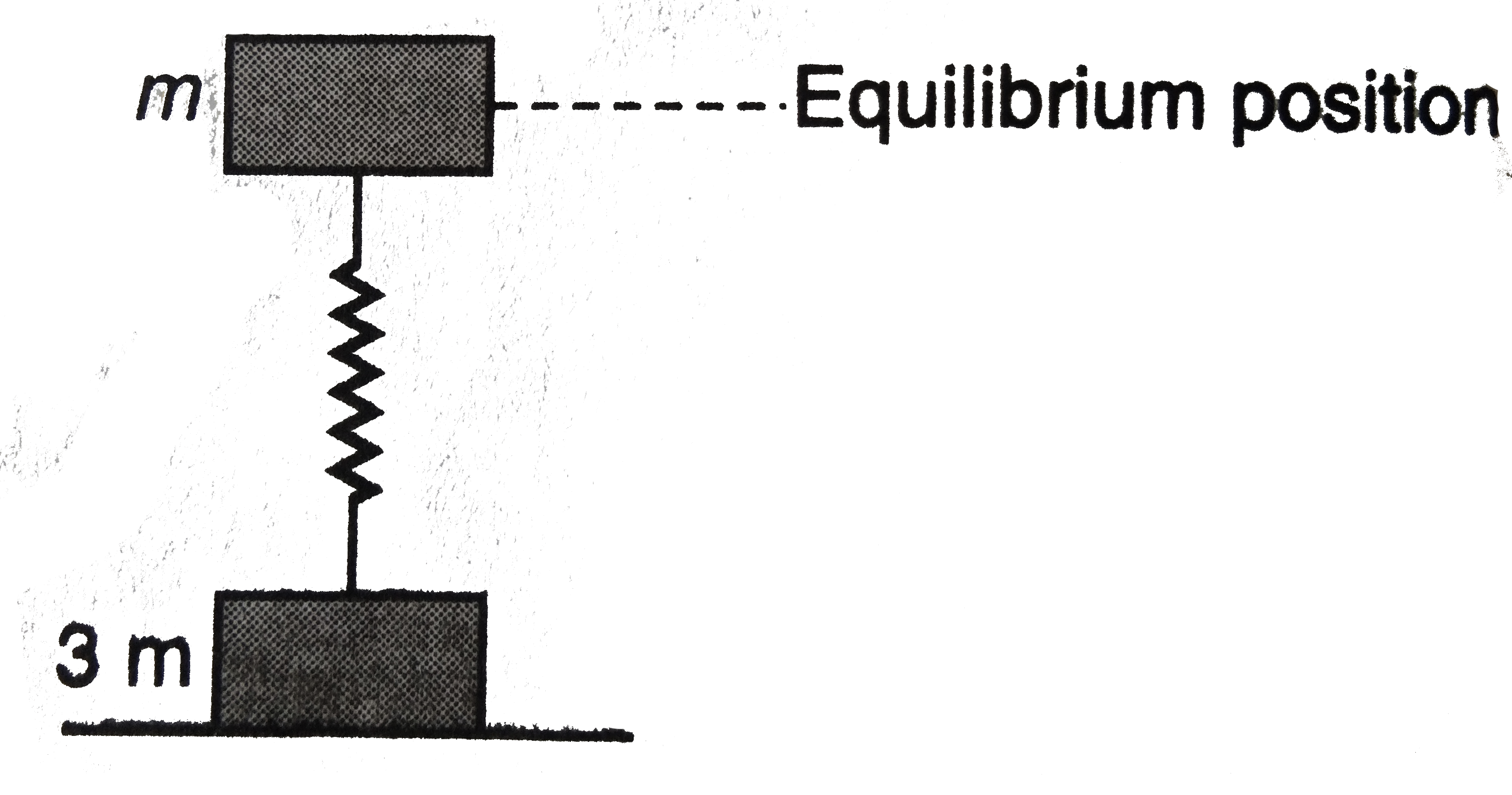 .
.
kδ0=mg
or δ0=mgk
where, δ0=compression
(b) δTotal=δ+δ0=3mgk
Fmax=kδmax=k(3mgk)=3mg(downward)
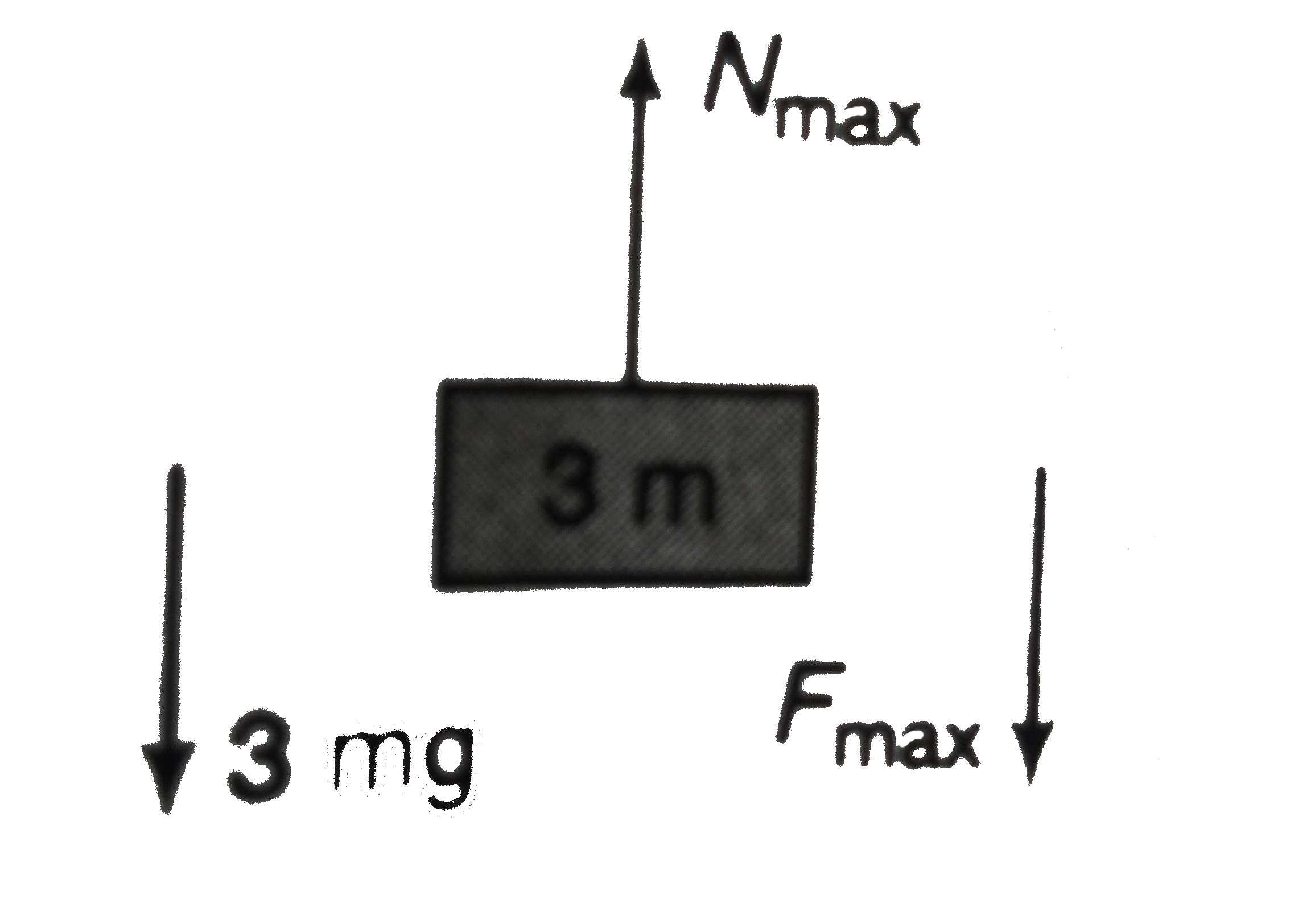
∴Nmax=3mg+Fmax=6mg
(d) If δ>4mgk, the upper block will move a distance x>4mgk−δ0 or x>3mgk from natural length.
Hence in this case, extension
x>3mgk
or F=kx>3mg (upward on lower block)
So lower block will bounce up.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Subjective
15 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 objective
30 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
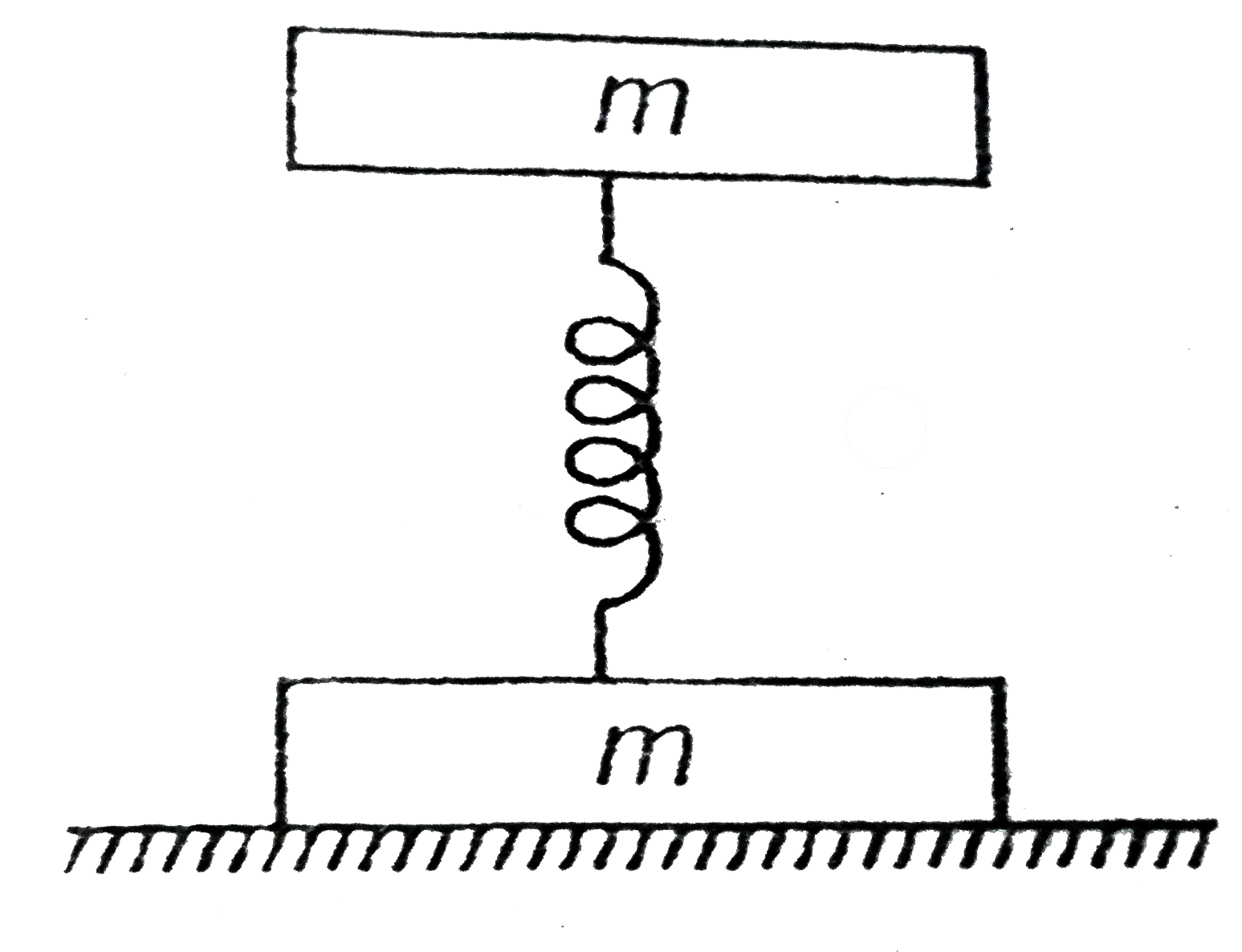
Figure shows two discs of same mass m. They are rigidy attached to a spring of stiffness k. The system is in equlibrium. From this equilibrium position, the upper disc is pressed down slowly by a distance x and released. Find the minimum vlue of x, if the lower disc is just lifted off the ground.
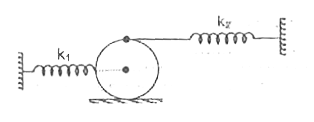
View SolutionA disk of mass m is connected to two springs of stiffness k1andk2 as shown in the figure. Find the angular frequency of the system for small oscillation. Disc can roll on the surface without slipping
View Solution
Knowledge Check
A disc of mass m is connected with an ideal spring of stiffness k. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:
 AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθk
AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθkA uniform circular disc of mass 'm' and radius 'R' is placed on a rough horizontal surface and connected to the two ideal non-deformed spring of stiffness k and 2k at the centre 'C' and point 'A' as shown . The centre of the disc is slighty displaced horizontally from equilibrium positon and then released, then the time period of small oscillation of the disc is (there is no slipping between the disc and the surface).
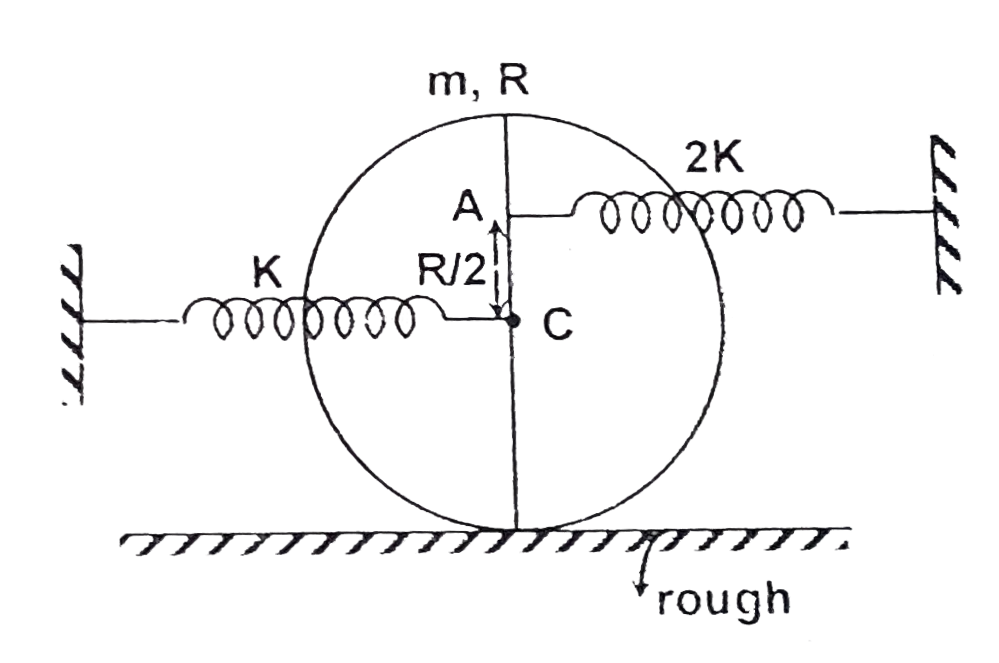 A2π√5m7kB2π√3m7kC2π√5m11kD2π√3m11k
A2π√5m7kB2π√3m7kC2π√5m11kD2π√3m11kIn the figure shown the spring constant is K the mass of the upper disc is m and that of the lower disc is 3m the upper block is depressed down from its equilibrium position by a distance δ=5mg/k and released at t=0 find the velocity of m when normal reaction on 3m is mg
 AzeroBg[m/k]1/2C2g[m/k]1/2D4g[m/k]1/2
AzeroBg[m/k]1/2C2g[m/k]1/2D4g[m/k]1/2
A disc of mass m2 is placed on a table. A stiff spring is attached to it and is vertical. The other end of the spring is attached to a disc of mass m1 What minimum force should be applied to the upper disc to press the spring such that the lower disc is lifted off the table when the external force is suddenly removed?

View Solution
A uniform disc of mass m and radius R is pivoted smoothly at its centre of mass. A light spring of stiffness k is attached with the dics tangentially as shown in the Fig. Find the angular frequency in rads of torsional oscillation of the disc. (Take m=5kg and K=10Nm.)
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank is
View SolutionA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank is
View SolutionOne end of spring of spring constant k is attached to the centre of a disc of mass m and radius R and the other end of the spring connected to a rigid wall. A string is wrapped on the disc and the end A of the string (as shown in the figure) is pulled through a distance a and then released.
The disc is placed on a horizontal rough surface and there is no slipping at any contact point. What is the amplitude of the oscillation of the centre of the disc?

View Solution
