A disc of radius and mass is projected on to a horizontal floor with a backward spin such that its centre of mass speed is and angular velocity is . What must be the minimum value of so that the disc eventually returns back?

Initally there is forward slipping, therefore, friction is backwards and maximum.
Let velocity becomes zero in time and angular velocity becomes zero in time
then
or ..(i)
and ltbr> or
here
...(ii)
disk will return back when
or
or
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to the plane with angular velocity ω. Another disc of same mass but half the radius is gently placed over it coaxially. The angular speed ofthe composite disc will be:
View Solution
Knowledge Check
A uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position ifAω0R=2V0Bω0R<2V0Cω0R>2V0DData insufficientA uniform disc of mass m and radius R is released gentiy on a horizontal rough surface. Such that centre of the disc has velocity V0 towards right and angular velocity ω0 (anticlockwise) as shown.

Disc will certainly come back to its intial position ifAω0R>2V0Bω0R=2V0Cω0R<2V0DIt is impossibleA uniform circular disc of radius r is placed on a rough horizontal surface and given a linear velocity v0 and angular velocity ω0 as shown. The disc comes to rest after moving some distance to the right. It follows that
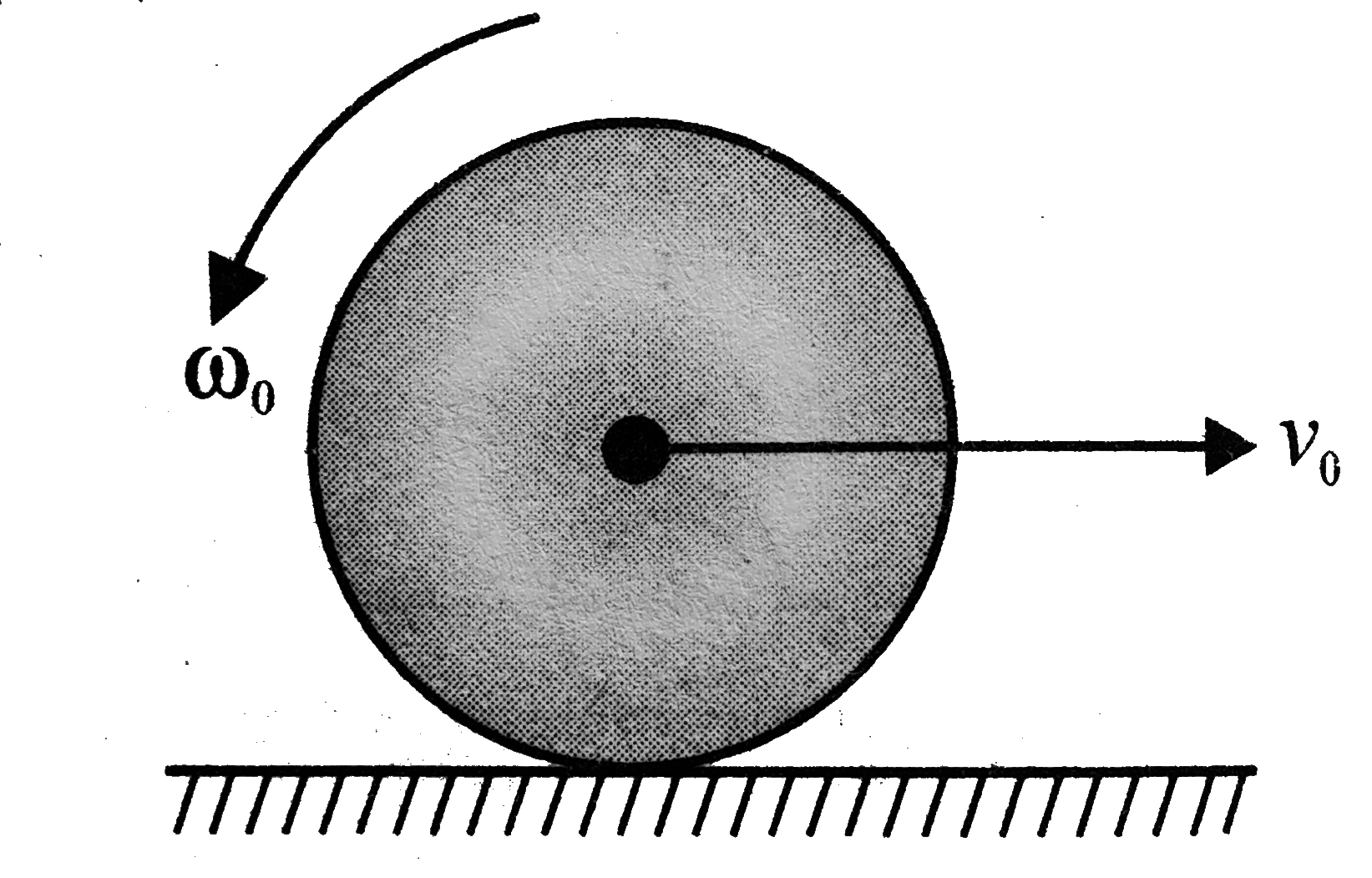 A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
A3v0=2ω0rB2v0=ω0rCv0=ω0rD2v0=3ω0r
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is
View SolutionA thin and circular disc of mass m and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . If another disc of same dimension but mass ml4 is placed gently on the first disc co-axially, then the new angular velocity of the system is
View SolutionA uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
View SolutionA disc of radius r rolls without slipping on a rough horizontal floor. If veloocity of its centre of mass is v0, then velocity of point P, as shown in the figure
(OP=r/2 and ∠QOP=60∘)is

View Solution
