A disc of radius R starts at time t=0 moving along the positive x-axis with linear speed v and angular speed ω. Find the x and y coordinates of the bottom most poitn at any time t.
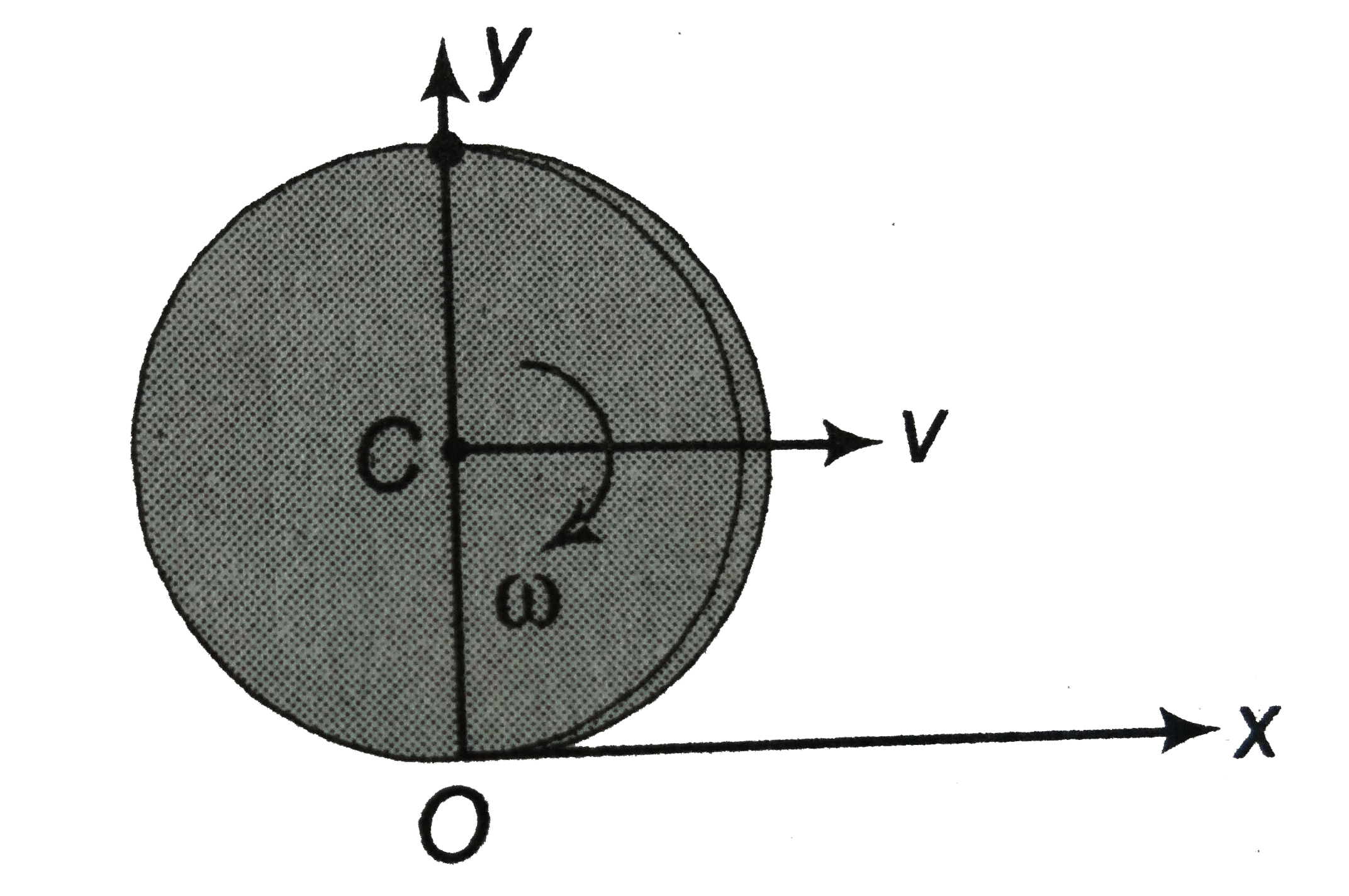
(x,y)≡(vt−Rsinωt,R−Rcosωt)
(x,y)≡(2vt−Rsinωt,R−Rcosωt)
(x,y)≡(vt−Rsin2ωt,R−Rcosωt)
(x,y)≡(Rsinωt,R−Rcosωt)

At time t the bottommost poit will rotate and angle θ=ωt with respect to the centre of the disc C. The centre C will travel a distance s=vt.
In the figure, PQ=Rsinθ=Rsinωt and CQ=Rcosθ=Rcosωt
coordinates of point P at time t are x=OM−PQ=vt−Rsinωt
and y=CM−PQ=R−Rcosωt
∴(x,y)=(vt−Rsinωt,R−Rcosωt)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A disc of radius R start at time t=0 moving along the positive X-axis with linear speed v and angular speed ω. Find the x and y-coordinates of the bottommost point at any time t.

View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View SolutionTwo identical discs of same radius R are rotating about their axes in opposite directions with the same constant angular speed ω . The discs are in the same horizontal plane. At time t=0 , the points P and Q are facing each other as shown in the figure. The relative speed between the two points P and Q is vr. In one time period (T) of rotation of the discs , vr as a function of time is best represented by
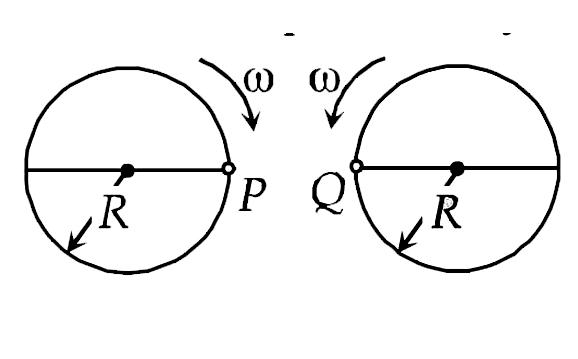
View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA particle moves along a circle of radius R with a constant angular speed ω . Its displacement (only magnitude) in time t will be
View SolutionThe magnitude of displacement of a particle moving in a circle of radius a with constant angular speed ω varries with time t is
View SolutionA particle starts from the origin at time t = 0 and moves along the positive x-axis. The graph of velocity with respect to time is shown in figure. What is the position of the particle at time t = 5s ?

View Solution
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View Solution
A cicular disc of mass m and radius R is set into motion on a horizontal floor with a linear speed v in the forward direction and an angular speed ω=vR in clockwise direction as shown in figure. Find the magnitude of the total angular momentum of the disc about bottom most point O of the disc.
View SolutionA particle located at x=0 at time t=0, starts moving along with the positive x−direction with a velocity 'v' that varies as v=a√x. The displacement of the particle varies with time as
View Solution
