A disc rolls on ground without slipping. Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ. Suppose, vP is the speed of this point. Then, match the following columns
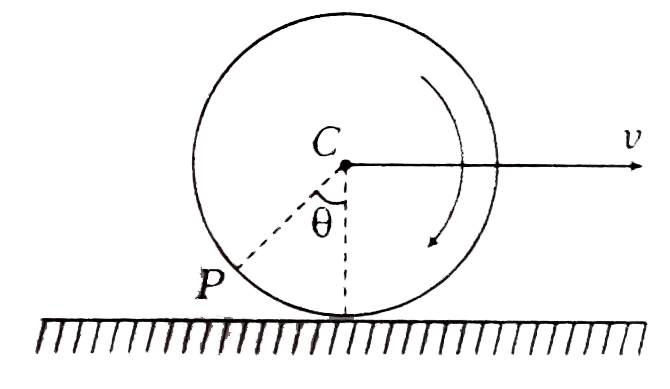
Column-IColumn-II(A)Ifθ=60∘(p)vP=√2v(B)Ifθ=90∘(q)vP=v(C)Ifθ=120∘(r)vP=2vD)Ifθ=180∘(s)vP=√3v
The correct Answer is:(A→q,B→p,C→s,D→r)
In gerenal as vP=2vsin(θ2)
If θ=90∘, then vP=2vsin(60∘2)=2v×12=v
⇒(A)→(q)
If θ=90∘, then vP=2vsin(90∘2)=2v×1√2=√2v
⇒(B)→(p)
If θ=120∘, then vP=2vsin(120∘2)=2v×√32=√3v
⇒(C)→(s)
If θ=180∘, then vP=2vsin(180∘2)=2v⇒(D)→(r).
Topper's Solved these Questions
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (A) Chapter Exercises
83 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
Similar Questions
A disc rolls on ground without slipping . Velocity of centre of mass is v. There is a point P on circumference of disc at angle θ . Suppose vp is the speed of this point. Then, match the following the following table.

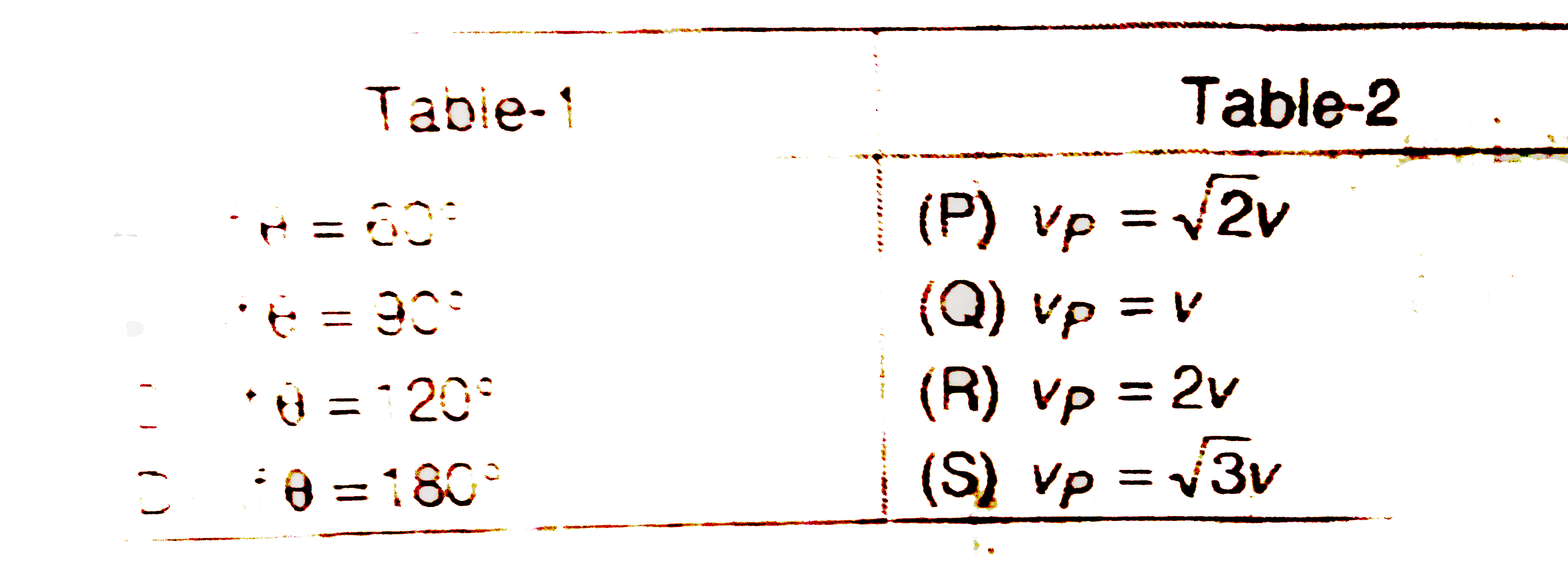
View SolutionA vector has a magnitude x . If it is rotated by an angle θ then magnitude of change in vector is nx. Match the following two columns.
Column I Column II(A)θ=60∘(P)n=√3(B)θ=90∘(Q)n=1(C)θ=120∘(r)n=√2(D)θ=180∘(s)n=2
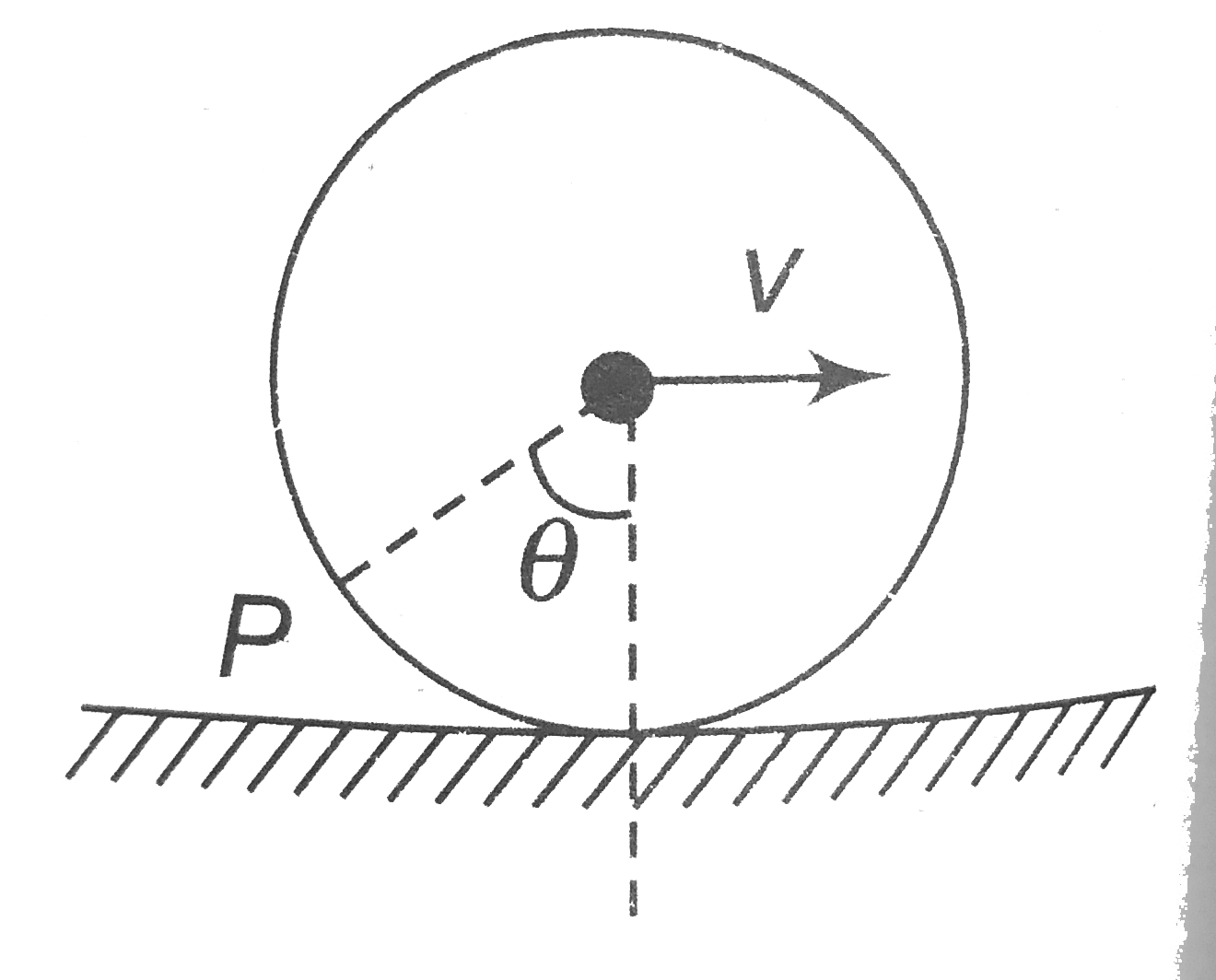
View SolutionA hoop rolls on a horizontal ground without slipping with linear speed v. Speed of a particle P on the circumference of the hoop at angle θ is :
View SolutionA disc is rolling without sliding on a horizontal surface. Velocity of the centre of the disc is V. Then the maximum relative sped of any point on the circumference of the disc with respect to point P is.

View SolutionIf θ is the abgle between two vectors A and B , then match the following two columns.
Column I Column II(A)A.B=|A×B|(P)θ=90∘(B)A.B=B2(Q)θ=0∘or180∘(C)|A+B|=|A−C|(r)A=B(D)|A×B|=AB(s)None
View SolutionA disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is

View SolutionA ring rolls without slipping on the ground. Its centre C moves with a constant speed u.P is any point on the ring. The speed of P with respect to the ground is v.
View SolutionIn the diagram shown in figure mass of both the balls in same. Match the following columns.
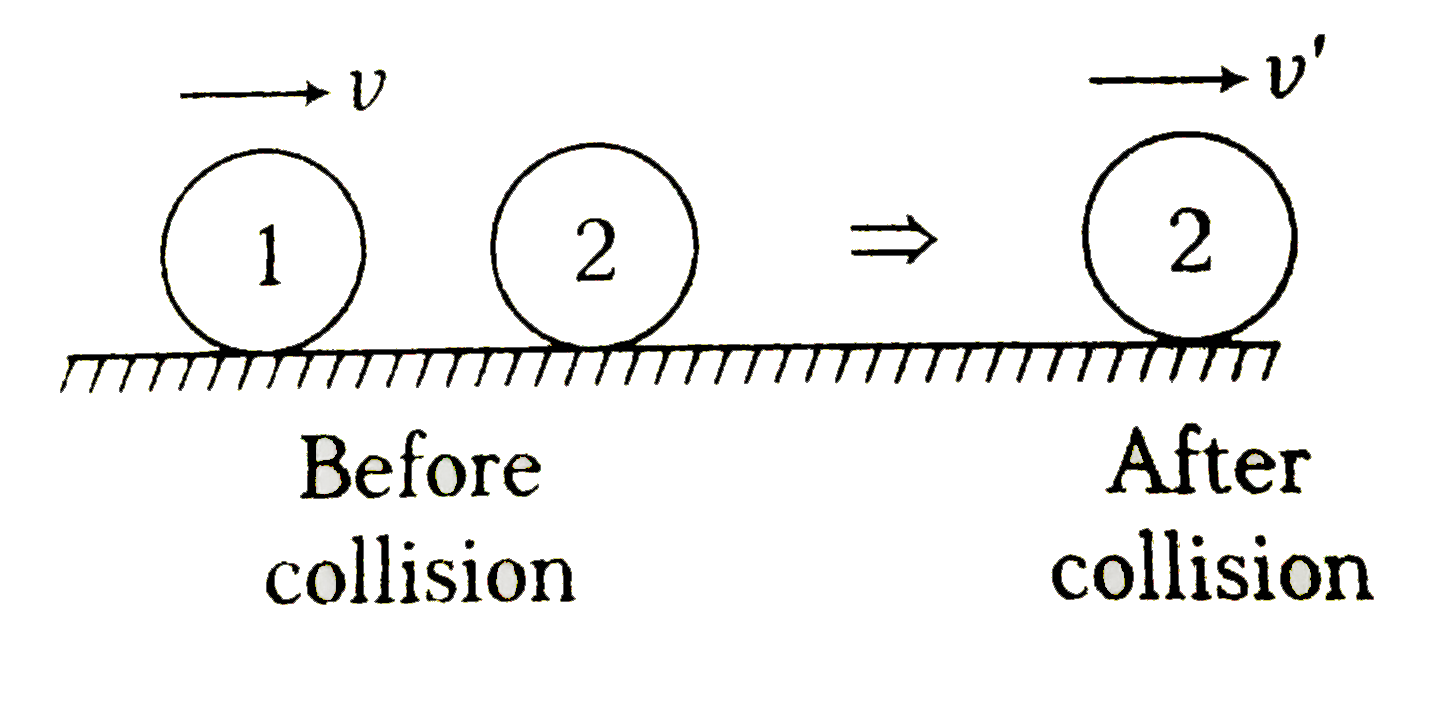
Column1Column2A Forv′=vP e=0B Forv′=v/2Q e=1C Forv′=3/4vR e=1/2-(S data is insufficient
View SolutionIn the circuit shown in figure, E = 10 V, r = 1Ω,
R = 4Ω and L = 5H. The circuit is closed at time t = 0.
Then, match the following two columns.
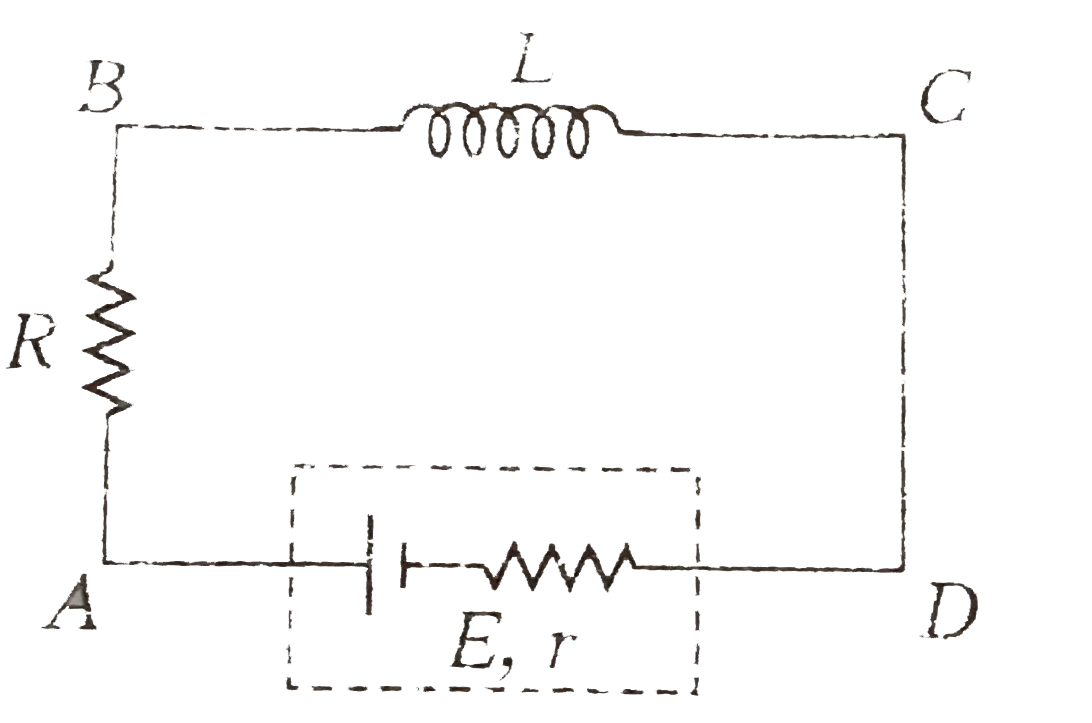
Column IColumn IIA.VAD at t = 0p4VB.VBC at t = 0q8VC.VAB at t =∞r.0VD.VAD at t=∞s.10V
View SolutionLet V and E denote the gravitational potential and gravitational field at a point. Then, match the following columns
Column-IColumn-II(A)E=0,V=0(p)At centre of spherical shell(B)E≠0,V=0(q)At centre of solid sphere(C)V≠0,E=0(r)At centre of circular ring(D)V≠0,E≠0(s)At cetre of two point masses of equal magnitude(t)None
View Solution
